重构二项式树降低能耗

无线传感器网络中面向延迟感知和高效能的数据聚合的重构二项式树

1. 引言

无线传感器网络（WSNs）由大量无线传感器节点组成，用于从其感知区域收集信息。在无线传感器网络中，传感器节点为电池供电，通常部署在恶劣环境中。许多方案被提出以减少无线传感器网络中的能量消耗和数据聚合延迟[1‐3]。其中，聚类和数据聚合算法得到了广泛研究，可减少传感器节点之间的数据传输[4‐5]。传感器节点通过将多个数据包合并为单个数据包来实现数据聚合。文献中先前的方案在每个节点的能量消耗方面存在不平衡问题，因为所有节点的传输范围不均衡，且簇头（CH）比簇成员（CMs）承担更多工作量[6]。

现有的数据聚合与聚类算法已被研究用于解决节能问题。这些算法在能量消耗、能量均衡和数据聚合延迟方面取得了改进。诸如LEACH[1]和PEDAP[2]等能量消耗最小化算法通过限制节点长距离传输来实现节能，从而延长了网络生命周期，但导致数据聚合延迟的效率降低。通过采用DADC[3]中提出的高效延迟网络结构，数据聚合延迟得到了显著改善。然而，DADC方案未考虑能量效率问题，仅专注于数据聚合延迟。因此，若实际部署，其在能量效率方面并不理想。

在构建延迟高效的网络结构以提升能量效率时，DADC和DEDA[7]均考虑了节点之间的距离。然而，在树构建的最后阶段，相连节点之间的通信距离比其他节点更远。

所提出的方案改进了由现有算法组织的网络中的能量效率，并减少了数据聚合延迟。当节点插入或删除时，现有树结构算法通过使用旋转方法保持树的平衡，且不影响周围结构。

本文提出了一种类似于AVL树等现有树结构算法中旋转方法的方案。在构建二项树[8]后，通过部分交换传感器节点的角色来降低树成本，同时保持树结构不变。通过应用RBT方案可以在保持树结构完整的前提下降低树成本。因此，在保留现有算法优势的同时实现了性能提升。如果将本方案中的父子角色交换方法应用于已构建的二项树，则树的能量效率性能将进一步提高。

本文的其余部分组织如下。在第2节中，我们讨论相关工作。第3节描述了所提出的RBT方案。第4节展示了我们的仿真和性能评估。最后，我们在第5节总结了我们的工作。

2. 相关工作

聚类方法中的单个簇是通过将多个节点分组形成的。每个簇包含一个簇头（CH），其余节点成为簇成员（CMs）。每个节点执行数据收集和聚合，以减少能量消耗和数据传输延迟。本文研究了数据聚合和聚类算法，如DEDA、LEACH、PEDAP和DADC。LEACH是一种通常用于分布式环境的聚类算法。在该算法中，每个传感器的角色是随机确定的。在簇头节点确定后，簇内的其他节点成为簇成员。每个节点接收、收集并聚合数据。其中，簇头需要聚合和收集大部分数据，并且只有簇头可以与基站（BS）通信。因此，簇头的能量消耗最为严重。LEACH随机确定节点角色。由于LEACH在随机选择簇头时未考虑节点的能量水平，因此不能被视为最优方案。

PEDAP旨在实现无线传感器网络中的能量效率。PEDAP使用最小生成树（MST），这是一种单链式簇结构方案，可最小化节点之间的通信距离。LEACH和PEDAP算法在数据聚合延迟方面效率不高，仅考虑了能量效率。

A. 延迟感知数据收集（DADC）

在DADC中，程等人提出了一种新型的高效延迟网络结构，该结构被证明可提供最小的数据聚合延迟。DADC方案在分布式计算环境中采用自底向上方法构建树形结构。DADC方案通过与邻近节点以及每个传感器节点所在区域内的节点交换其位置和ID等信息。信息交换完成后，每个簇头按照随机退避的固定顺序向最近的邻近簇头发起连接消息，两个簇头通过连接形成汇聚簇。如果节点数量不同，相关簇头将发送“拒绝消息”，收到拒绝消息的簇头则向第二近的簇头发送连接消息。若在指定范围内没有可汇聚的簇，则通过扩大范围向更远的簇头发送连接消息。若在整个网络范围内均无其他簇可供汇聚，则最终由簇头与基站建立连接，形成二项树。在簇汇聚过程中，由于两个簇头中的一个被随机选为汇聚后簇的簇头，可能导致网络构建过程中节点间的传输距离较远。因此，DADC方案在网络能量节约和节点能量消耗均衡性方面提升了性能。

B. 延迟最小化的节能数据聚合（DEDA）

DEDA方案比DADC方案更高效地改善了能量消耗，并保持了DADC方案在数据聚合延迟方面的改进。DEDA的簇形成阶段分为三个步骤。第一步，每个节点成为一个独立的簇，并分配簇层级。簇的层级由簇内的节点数量决定。DEDA方案的退避机制优先考虑距离基站最远的簇头。由于退避机制，当簇头将其消息转发给最近的邻居时，相同层级的簇会合并。在第二步中，决定是否进一步合并通过簇内簇头之间使用链路权重函数进行通信。在第三步中，通过簇间的收敛形成更大的簇。如果在网络中重复上述三个阶段后已没有可继续收敛的簇，则树构建完成。DEDA方案在形成簇时考虑了簇头之间以及簇头与基站之间的较短距离。然而，由于DEDA存在约束，即簇只能在同一层级的两个簇之间进行收敛，因此会形成较长链路。

3. 重构二项式树

A. 预备知识

所提出的方案通过节点之间的角色交换来降低树成本，同时保持已构建的树结构不变。当网络中插入或删除节点时，会在AVL树和红黑树等若干树形数据结构中执行树旋转[8]。这些树通过使用不影响周围结构的旋转方法来保持树的平衡。对于AVL树而言，每个节点的左子树和右子树的高度保持平衡。当插入或删除节点时，需要重新平衡高度，因此AVL树适用于插入和删除操作较少而搜索操作较多的数据结构。AVL树是一种二叉树，也是一种平衡树，其构成的左子树和右子树的高度差小于或等于1。AVL树旨在减少二叉树内的搜索时间。而在普通二叉搜索树中，由于插入或删除操作，树的高度平衡无法得到维持。在AVL树中，当节点被插入或删除时，通过旋转重构树以维持高度的平衡。

所提出的方案对现有的二项树进行重建。网络中的二项树由 $N$ 个随机部署的无线传感器组成。部署完成后，传感器节点和基站的位置固定。使用所提出的方案，在树重建完成后，仅节点的角色发生变化，而其物理位置不变。节点的能量消耗与传输距离的平方成正比。图1展示了一个二项树的示例。该二项树将节点数量（$N$）限制为 $2^r$。每个节点的秩从0到 $r$。秩由子节点的数量决定。具有 $r$ 的节点可以拥有子节点秩为0到 $r-1$。叶节点的秩为0，而簇头在网络中具有最高的秩。

在树构建阶段的簇收敛过程中使用秩，并指示 $T$ 时隙，每个节点被分配 $r+1$ 时隙。在此树结构中，每个节点根据分配的时隙被调度发送数据。通过这种调度，可以避免多个节点同时传输到单一目标节点所引起的碰撞。

本文所采用的假设如下：网络中的节点数量限制为 $2^r$。所有数据包具有相似大小，且从一个节点到其父节点的数据传输在一个时隙内完成。每个传感器在一个时隙内只能接收一个数据包。每个节点对接收到的数据进行聚合，以减少网络中的数据包数量，并将聚合数据发送给邻近节点。每个传感器节点一次只能与一个传感器通信。本文假设传感器的能量消耗与其传输距离的平方成正比。边成本定义为树中两个节点之间通信距离的平方，树成本定义为边成本的总和。

B. 交换

本文提出了一种通过重建二项树来减少具有长传输距离的节点数量，从而降低网络能量消耗的方案。该重建通过两个节点之间的角色交换方法实现。本文所提出的方案采用父节点和子节点之间的角色交换方法。该角色交换方案的工作流程如下：第一步，构建二项树以应用所提出的方案；在构建二项树时，树构建方法不受限制。第二步，应用所提出的方案对二项树进行重建；从树内所有节点中选择一个节点进行角色变更，并在节点之间交换角色，同时保持已构建树的结构不变。第三步重复执行，直到边成本无法进一步降低为止。

公式1比较了所提出的方案应用前后 $\epsilon$ 的边成本。如果 $\epsilon$ 连续次数超过 $\epsilon_0$，则结束所提出的方案。在本文中，$\epsilon$ 是方法收敛的一个变量，且取决于实验。树成本表示为 $\alpha$。

$$
\epsilon_i = \frac{\alpha_{i-1} - \alpha_i}{\alpha_{i-1}} \leq \epsilon \tag{1}
$$

从所有节点中，所提出的方案计算在三个步骤开始时可以降低的边成本。根据计算出的边成本，选择能够最大程度减少边成本且边成本最低的节点。如果在节点间进行角色交换时，由于周围节点的影响导致增量值发生变化，则下一次角色交换可能在未识别信息的情况下进行。此类问题可能会增加边成本，并影响重建次数。因此，在角色交换中选择的节点不应受到周围节点的影响，且仅需执行必要的节点角色交换。所提出的方案基于低复杂度设计约束。

所提出的方案采用P‐交换，这是一种在特定节点与其父节点之间交换角色的方法。根节点不能被选为P‐交换的节点u。首先，设P和G分别为u的父节点和祖父节点。P‐交换将秩（r）大于u的u兄弟节点重新组织为u的子节点。如果P不是根节点，u成为G的子节点，P成为u的子节点。在执行P‐交换时，链路数量保持不变，仅改变其长度。因此，除与父节点相连的链路外，其余链路均不发生变化，边的数量也不受影响；因此，树结构保持不变，周围节点不受影响。

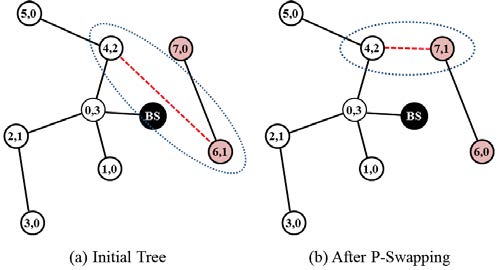
例如，如果u是图2中的节点7，则节点7与其父节点6交换角色。由于节点6和7交换了它们的角色，两者之间的边没有变化，而边(4, 6)变为边(4, 7)。同时，节点6和7的秩也相互交换。换句话说，节点7的秩从0变为1，节点6的秩从1变为0。

$$
\delta(u) = -E(Pr(u), Gr(u)) + E(Gr(u), u) - \sum_{w \in ch(Pr(u)), rank(w) > rank(u)} (E(Pr(u), w) - E(u, w)) \tag{2}
$$

树成本在节点之间角色变更前后进行计算，其差值表示为 $\delta(u)$。如果 $\delta(u)$ 为负值，则总边代价可以减少。在图2中，P‐交换情况下，仅与节点4相连的边(0, 4)和(4, 6)发生变化，且 $\delta(u)$ 通过公式2计算。在公式2中，$E(i, j)$ 表示两个节点i和j之间的边。w表示秩高于u的节点。

4. 性能评估

A. 仿真方案与环境

本节展示了所提出的方案与现有方案的性能比较。基于C++开发了仿真环境以进行性能评估。每个具有相同传输半径的节点分布在不同大小的方形网络中，且节点部署后位置保持不变。节点数量以 $2^p$ 的形式从16增加到64，每次仿真执行50次。树成本通过 $\sum d_e^2$ 进行评估。

比较了使用所提出的方案以及现有的树重建方案对二项树进行重建后的树成本。所使用的方案为DADC和DEDA，而所提出的方案则利用DADC和DEDA构建的树进行重建。

B. 评估结果

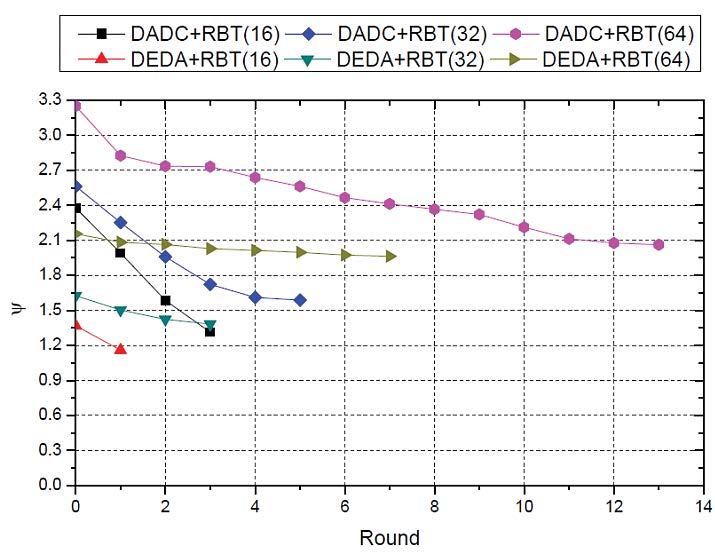
图3显示了使用DADC和DEDA的所提出方案重建二项树的结果。比较了分别由16、32和64个节点组成的网络。在图3中，该图显示了DADC和DEDA的起始点存在很大差异。总体而言，当使用DADC构建树时，$\alpha$ 更高，并且与 $\alpha$ 以及DEDA在树构建过程中消耗的轮数相比，使用的轮数更多。换句话说，由DADC构建的树更加复杂，通过重建可以减少更多的 $\alpha$。轮数也显示出巨大差异，具体取决于早期阶段树的构建方式，最终在收敛情况下所减少的 $\alpha$ 也因此不同。当节点数量较少时，所需的轮数也较少，因此难以降低边成本。结果，根据起始点的不同，收敛后的边成本可能存在差异。然而，随着节点数量的增加，如果应用所提出的方案进行重建，则无论采用何种初始树构建方案，最终的边成本都可以收敛到相近的水平。这意味着，如果应用所提出的方案，无论初始树构建方案如何，$\alpha$ 都可以降低到一定程度。

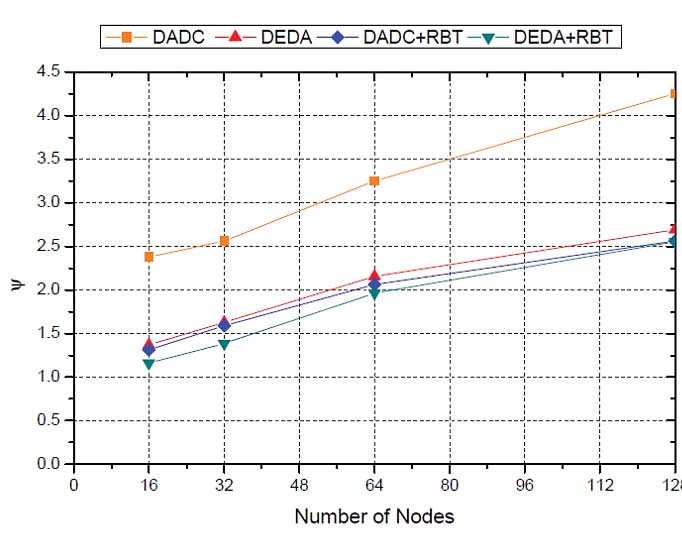
在图4中，DADC方案显示出最高的边成本，因为它仅关注数据聚合延迟，而在树构建阶段未考虑节点之间以及节点与基站之间的距离。与此同时，DEDA方案在构建树时考虑了节点间的距离，因此与DADC方案相比，边成本显著降低。

当网络内的节点数量为16时，应用所提出的方案的两种情况下的轮次结束时间有所不同；尽管节点数量增加，结果仍相似。最终，本文所提出的方案显著降低了边成本，且在重建后数据聚合延迟保持不变，因为在使用DADC和DEDA方案进行重建时，树结构得以维持。

5. 结论

本文提出了一种在进行数据聚合的同时降低网络能量消耗和延迟的方案。所提出的方案是限制重建方法P‐交换。DADC和DEDA方案用于树结构的初始构建，然后将所提出的方案应用于已构建的树。仿真结果表明，使用DADC和DEDA构建树的平均能量消耗分别降低了45.84%和14.28%，并且由于保持了树的结构，数据聚合延迟维持在最优水平。此外，通过使用所提出的方案对任何其他方案生成的树进行重建，可将树的边成本降低到一定水平。未来，我们计划将研究扩展到除DADC和DEDA构建的二项树之外的其他树结构。