py实现牛顿迭代法（sympy实现计算函数值和求导）

最新推荐文章于 2025-10-30 20:06:41 发布

原创

最新推荐文章于 2025-10-30 20:06:41 发布 · 2.5k 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#牛顿迭代法 #python

本文介绍了如何使用Python的sympy库实现牛顿迭代法来求解非线性方程，详细讲解了计算函数值、求导数的过程，并探讨了多元函数的处理以及牛顿迭代法的具体实现，包括最大迭代次数和精度控制。

牛顿迭代法

求解非线性方程的方法，属于迭代法的一种，原理的话：
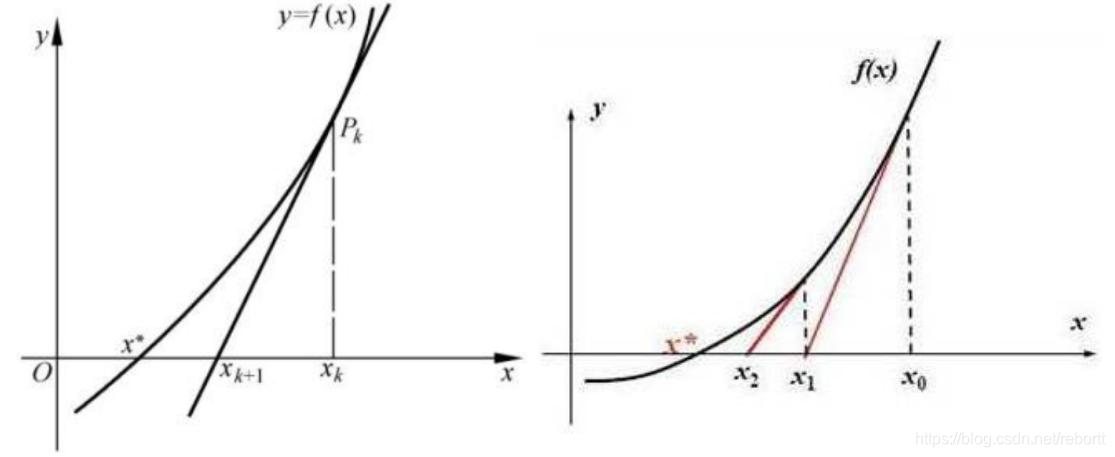
在这里插入图片描述
x^*是这个方程的根，我们在旁边找一个点x_k，根据这个点的函数值和导数值，我们可以计算出这条直线和x轴的交点x_k+1，然后将x_k+1作为下一个x_k迭代计算，就能得到答案。

我们将方程整理一下，有：
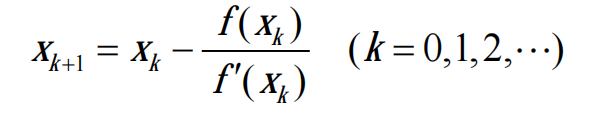
在这里插入图片描述
实际上实现还是很简单的，唯一的难点就是怎么计算函数值和导数值。

计算函数值和导数值

如果是函数值的话，math包中有cos、sin和exp能解决问题，但是还是解决不了求导过程，这时我们就需要使用强大的sympy了。

计算函数值

import sympy as sp
x0 = 1
x = sp.symbols('x')
y = x**2-2*x*sp.exp(-x)+sp.exp(-2*x)
print( float(y.evalf

最低0.47元/天解锁文章

确定要放弃本次机会？

福利倒计时

: :

立减 ¥

普通VIP年卡可用

立即使用

筱羊冰冰

关注关注

4
点赞
踩
9

收藏

觉得还不错? 一键收藏
1
评论
分享

复制链接

分享到 QQ

分享到新浪微博

扫一扫
举报

举报

专栏目录

sympy 计算表达式

jacke121的专栏

08-21

3235

from sympy import * def test_matrix(): A = Matrix([[x, x*y], [sin(z)+4, x**z]]) sol = Matrix([[1, 2], [sin(3)+4, 1]]) f = lambdify((x,y,z), A, modules="sympy") assert f(1,2,3) == sol f = lambdify((x,y,z), (A, [A]), modules="sympy")...

Python01 二分法简单迭代法 Newton迭代法 (附代码)

weixin_42970036的博客

09-26

2390

1. 实验结果（1）在定义的方程类中设置需要求解的方程为：（2）调用方程类中定义的显示图像函数，显示曲线如下：（3）选择二分法求解，输入所需参数：精度要求和区间[a , b]，得到满足精度要求的方程的根及迭代次数；（4）选择简单迭代法求解，输入所需参数：精度要求和初始点 x0，得到每次迭、代的值及满足精度要求的方程的根；（5）选择 Newton 迭代法求解，输入所需参数：精度要求和初始点 x0 ，得到每次迭代的值及满足精度要求的方程的根； 2. 代码 main.py from unl_e

1 条评论您还未登录，请先登录后发表或查看评论

python求导函数的值_定义sympy函数导数的数值计算

weixin_39520393的博客

12-04

807

How can I define the numerical evaluation of a derivative of a function in sympy?I have some functions I can describe with splines for the function and it's derivative using scipy.interpolate.I want t...

牛顿迭代法

incipe

08-23

1725

牛顿迭代法（Newton’s method）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。当然，牛顿迭代法也是已知已知的实现求方根最快的方法之一。 ...

sympy入门——通过sympy计算数据

最新发布

weixin_52215381的博客

10-30

摘要：本文介绍了使用SymPy库进行符号计算的基础方法，包括代数方程定义、变量替换和数值计算转换。通过lambdify函数可将符号表达式转换为可计算函数，并演示了使用NumPy数组生成一维线图、二维网格图和三维散点图的可视化应用。文章还提到了SymPy的其他功能，如方程求解、展开、系数提取以及排列组合运算等。这些方法为机器学习中的函数计算提供了便捷的符号运算工具。

python|牛顿迭代

qq_56630261的博客

11-21

3316

@python牛顿迭代 前言前几天刷题时候看到一道题，就是不用任何内置函数与库，实现算一个数的根，第一反应就是二分法（前面文章有介绍，如有需要，请点击此处），后面在一众评论和题解中发现一个方法，叫做牛顿迭代，还蛮有意思的，下面，我们就一起来看一下牛爵爷的方法。 牛顿迭代解释牛顿迭代法（Newton’s method）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式，因

python实现牛顿法_牛顿法和最速下降法的Python实现

weixin_39562338的博客

11-21

1555

1 牛顿法1.1 牛顿法的Python程序from sympy import *import numpy as np# 假设多元函数是二维形式# x_init为二维向量(x1, x2)def newton_dou(step, x_init, obj):i = 1 # 记录迭代次数的变量while i 0.001):if i == 1:grandient_obj_x = np.array([valu...

Python实现自动求导：掌握数学表达式的符号计算

本资源中包含的两个压缩包子文件代码4-3 内点法.py和代码4-2 自动求导.py，提供了相关的Python代码示例和自动化求导的实现方法。" 知识点： 1. Python符号计算库：在Python中进行自动求导的常用库之一是SymPy库。...

M1 S2数值方法与科学计算课程资源

赛德尔法、共轭梯度法）、非线性方程的牛顿迭代法、插值与逼近方法（如拉格朗日插值、样条插值）、特征值问题的数值求解等。这些方法的设计不仅要考虑算法的准确性，还需关注其稳定性、收敛速度、计算复杂度以及对舍...

共轭梯度法与BFGS法Python实现

04-06

在优化领域，共轭梯度法（Conjugate Gradient Method）和BFGS法（Broyden-Fletcher-Goldfarb-Shanno Algorithm）是两种广泛使用的无约束优化算法，尤其适用于解决大型线性或非线性优化问题。这两种方法都是迭代算法...

python中的SymPy库函数的运用

qq_51478930的博客

03-21

8672

概念 sympy是一个Python的科学计算库，用一套强大的符号计算体系完成诸如多项式求值、求极限、解方程、求积分、微分方程、级数展开、矩阵运算等等计算问题。常用的sympy内置符号虚数单位i In [13]: import sympy In [14]: sympy.I Out[14]: I In [15]: sympy.I ** 2 Out[15]: -1 #求-1的平方根 In [16]: sympy.sqrt(-1) Out[16]: I 注；后面省略import sympy 自然对数的底

Python 基于sympy模块求极值导数偏导

weixin_44659084的博客

11-20

9497

sympy简介:sympy是一个Python的科学计算库，用一套强大的符号计算体系完成诸如多项式求值、求极限、解方程、求积分、微分方程、级数展开、矩阵运算等等计算问题。 1、求极限、求导、求偏导以及带值求导在这里插入代码import sympy #求极限 #设置符号变量Symbol只能创建一个变量 symbols 可一次定义多个变量 x1,x2,x3,x4=sympy.symbols('x1,x...

牛顿迭代多维+原理推导+导数矩阵不可逆+列文伯格

m0_53271604的博客

10-16

760

的二阶泰勒展开，后面的那一项是海森矩阵。矩阵的逆出现，其实就是求解方程组时出现的，所以矩阵不可逆的时候，可以直接用求解线性方程组的方法，求解出结果。三个方程两个未知量，有唯一解。这是两个函数了两个变量的情况，对于三个函数两个变量，牛顿迭代的雅可比矩阵不能求逆，多个函数的泰勒展开，其实就是这种单个函数泰勒展开的简单拼接而已。右边的增量的求解就不能用这个公式了呢。

牛顿插值法的Python程序

Fo*(Bi)的博客

06-02

3831

#牛顿插值，差商 from sympy import * x = Symbol('x') x_list = [1, 3, 2] y_list = [1, 2, -1] n = len(x_list) df_list = [y_list[0]] for k in range(1,n): df = 0 for i in range(k+1): X = 1 for j in range(k+1): if i == j: ...

[数值计算-9]：一元非线性函数求导数（数值微分）- 解析法与迭代法&Python法代码示例

文火冰糖（王文兵）的博客

08-20

1万+

作者主页(文火冰糖的硅基工坊)：https://blog.youkuaiyun.com/HiWangWenBing 本文网址：https://blog.youkuaiyun.com/HiWangWenBing/article/details/119813740 目录 1.一元n次非线性方程 1.1非线性函数 1.2 非线性函数案例 1.3 非线性函数的几何图形 2. 导数与解析法求导数 2.1 导数的源头和初心 2.2什么导数 2.3导函数 2.4 解析法求导数 3. 迭代法求导数的基本原理 ...

sympy 求导，并带入值进行计算