树的结构——基本概念和二叉树的五条性质

下面开始数据结构的树部分了。

树的定义

首先要有一个根节点，然后从左到右有若干个子树，子树之间不可以相交，且每一个子树都符合上述要求的（子树可以为空）叫做树。
在映射上树属于一对多的形式，之前的线性表可以理解为一对一的关系。
注意到，每一个子树也符合上述定义，说明树有一个递归的性质，后面会举例一些关于递归性质的例题

术语
一般将根节点称为第一层，
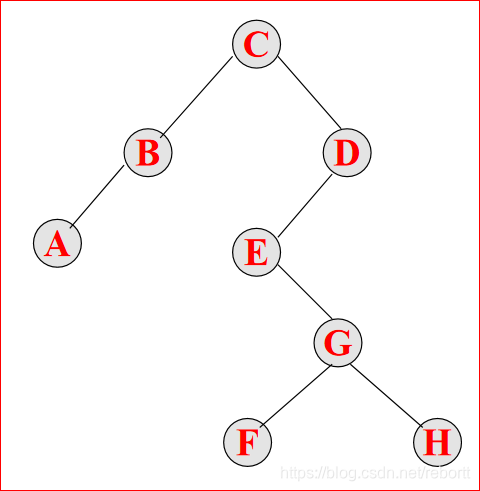
将距离根节点距离相同的结点放在一起构成一层，最大的层数叫做树高，（图中树高为5）
每一层结点个数的最大值为树宽。 （图中树宽为2）

双亲结点、孩子节点就不用说了吧。（话说parent为什么翻译成双亲，哪位dl在评论区解释一下 >_<）
子孙节点和祖先结点，比如C是E的祖先，反过来就是子孙了。

度：一个结点有多少个非空的孩子，一棵树的最大度是多少就是几叉树
叶子：孩子均为空
非终端结点：叶子集的补集。

森林：很多棵树构成的集合。

二叉树

一般来说，关于二叉树的研究还是比较多的。
根据上述说法，二叉树应该为每一个节点的度最大为2，不同的是二叉树的两个孩子是有区别的！
对于树来说，孩子在左边、右边、中间是一样的，但对于二叉树孩子在左边和在右边是截然不同的！

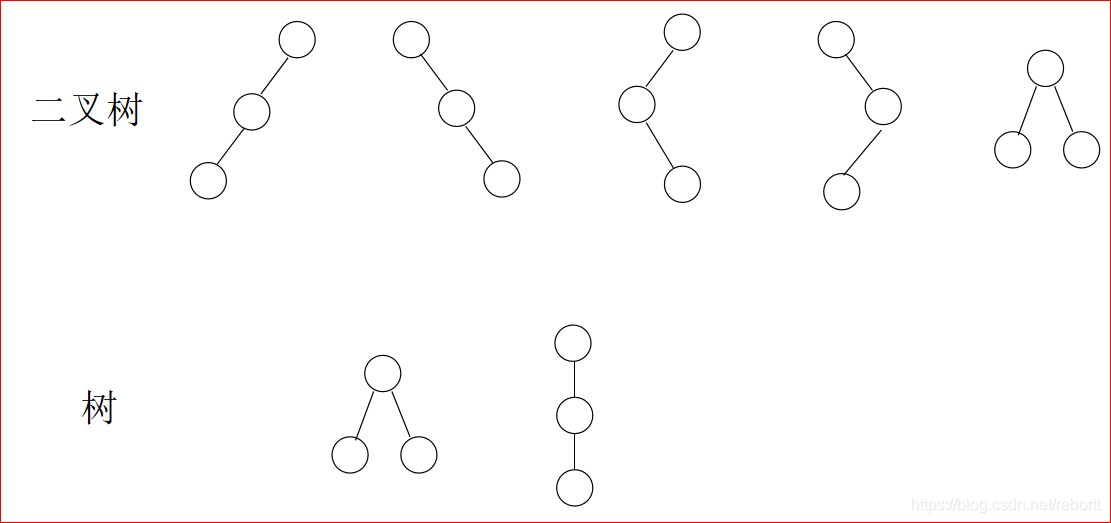
例：有三个节点的二叉树和树分别有多少种？
5和2，图是这样的：

二叉树的遍历方式

1. 先序遍历
2. 中序遍历
3. 后序遍历
4. 层次遍历
   上面三种情况差不多，第四种会有一点特殊。
   前面三个都是将一棵树分成三部分，根节点、左孩子、右孩子，且约束左子树的遍历要在右子树的前面，先中后指的是根节点。
   遍历的思想也是一种递归，从根开始，先序就要输出根，然后按先序的方式遍历左子树左子树全部结束后遍历右子树。
   层次是按层次遍历，从第一层的根节点到最后一层，在实现上有一点难度，具体代码将在后续推出。
   

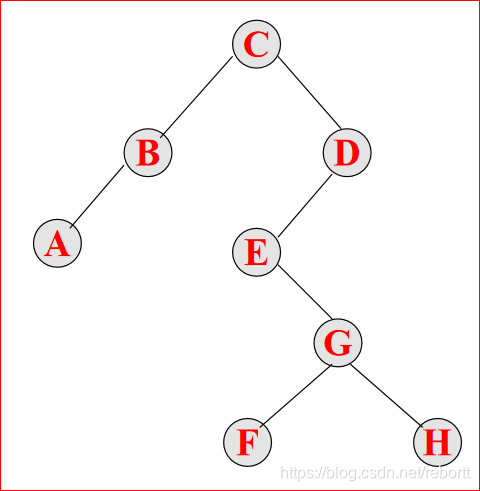
还是以这个图为例。
先序：cbadegfh
中序：abcefghd
后序：abfhgedc
层次：cbdaegfh

先序还好，中序和后序在有些时候经常会犯提前遍历根节点的问题，最好的方法就是记好定义，不断训练。

完全二叉树和满二叉树

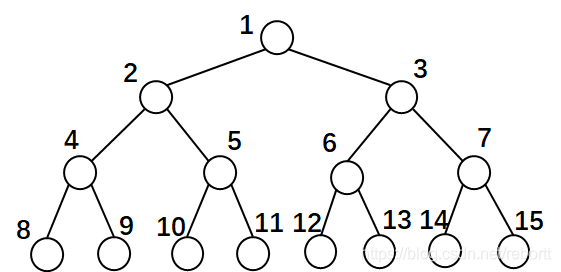
形如这样的（节点数最大）二叉树为满二叉树
而完全二叉树为层次遍历只有最后的元素可以缺失，中间的不可以缺失。

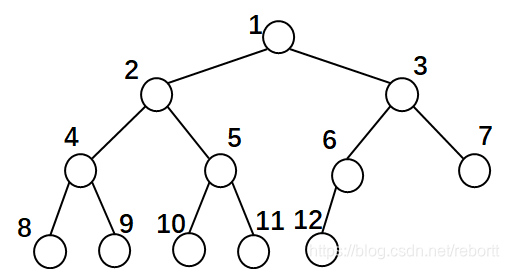
这个就是完全二叉树了，少了13、14、15

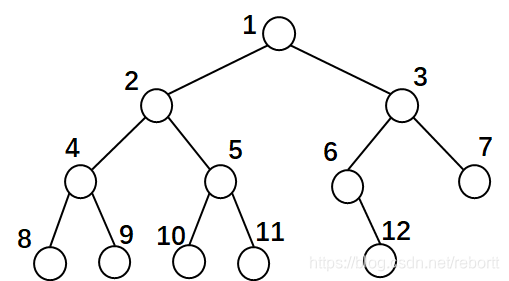
而这个，就不是完全二叉树，因为11、12中间应该还有一个结点

二叉树的5条性质

• 二叉树的第m层最多2^m-1个结点
• m层的二叉树最多结点数为2^m-1 //上面两个归纳法证明即可
• 有n个结点的完全二叉树层数为└ log2n┘+ 1（向下取整）
  证：设层数m，则满二叉树的节点数为(2^m-1-1,2^m-1]，且为整数，则为[2^m-1,2^m]，取2的对数得到答案
• 对任意非空二叉树，结点度数为2的节点个数为叶子结点数减一。
  证：以度数划分结点，叶子结点数设为n0，一度结点设为n1，二度节点设为n2。
  则总结点数为n0+n1+n2，但要知道度数是总结点数减一，因为每一个结点除了出度（刚才讨论的度）还有一个入度，减一是因为根节点没有入度，所以总结点数为出度+1=入度+1=2n2+n1+1
  联立两个式子，n0=n2+1 得证
• 将一棵完全二叉树按行遍历后对于第i个结点，他的左孩子是2i，右孩子是2i+1（如果存在这两个数）；同样一个结点（i！=1）的双亲应该是└i/2┘
  （这里再提一下，序号为总结点数的一半的结点应为叶子节点和非叶子节点的交界。）
  证明：归纳法
  
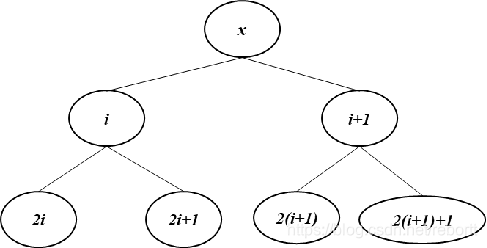
  考虑这图
  对于第一个结点（根节点），左孩子2，右孩子3，成立；
  如果i成立，i+1和i可能为一个结点的左右孩子，也可能是不同的双亲结点
• 第一种情况，按照图的结构，可证明
• 第二种情况类比这个图，也是可以证明的

这个东西的证明并不是单纯靠语言说明就行了的，还是需要自己的思考，多画图
（嗯，不是我说不明白）

（plus：这个东西虽然 看着没什么用，但是后来的线性存储这个定理还是很重要的，
另外这个定理其实对非完全二叉树也是成立的，就是有时候不确定有没有孩子）