利用拉格朗日中值定理求极限

最新推荐文章于 2025-03-06 22:31:50 发布

！@#￥asdgg321

最新推荐文章于 2025-03-06 22:31:50 发布

阅读量3.8w

点赞数 29

分类专栏：学习笔记

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/reachzh1/article/details/104917339

版权

学习笔记专栏收录该内容

3 篇文章

订阅专栏

本文介绍了一种使用拉格朗日中值定理求极限的方法，适用于等价无穷小替代、洛必达法则及泰勒公式难以处理的情况。该方法尤其适合处理两项相减且形式相同、随变量变化而趋近的极限问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

求极限常用等价无穷小替代、洛必达法则、泰勒公式等方法，有时候等价无穷小不能用，洛必达法则过于繁琐，泰勒公式法虽然强大但是相对麻烦。对有一些形式，使用拉格朗日中值定理非常便捷。下面举两个个例子：

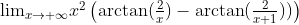
$$${\lim_{x \to +\infty}}$$ x^{2}\left ( \arctan( \frac{2}{x})-\arctan(\frac{2}{x+1})) \right )$

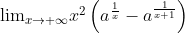
$$${\lim_{x \to +\infty}}$$x^{2}\left (a^{\frac{1}{x}}-a^{\frac{1}{x+1}} \right )$

这种形式的式子，很明显直接使用等价无穷小是不行的，洛必达法则又麻烦至极，泰勒公式做起来也不轻松。

我们发现上述式子有这样的特点：右侧减法式子里，两项的形式都非常类似，并且随着极限的趋向，两项越来越接近。这时候我们可以使用拉格朗日中值定理处理这个减法式子。

于是上述式子就可以变成（恒等变换）：

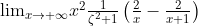
$$${\lim_{x \to +\infty}}$$ x^{2}\frac{1}{\zeta ^{2}+1}\left ( \frac{2}{x}-\frac{2}{x+1} \right )$

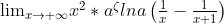
$$${\lim_{x \to +\infty}}$$ x^{2}*a^{\zeta}lna \left ( \frac{1}{x}-\frac{1}{x+1} \right )$

这个时候，随着x的增大，可以发现，拉格朗日中值定理作用的区间越来越小，最终可以确定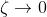 $\zeta\to0$ 然后接下来就非常好办了

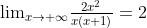
$$${\lim_{x \to +\infty}}$$ \frac{2x^{2}}{x(x+1)}=2$

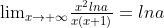
$$${\lim_{x \to +\infty}}$$ \frac{x^{2}lna}{x(x+1)}=lna$

上面的式子有这样的共性：1.存在两项相减因式且形式相同；2.随着x的变化，因式的两项越来越接近（ $\zeta$ 所在区间变小）

评论 3

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。