1、使用拉格朗日中值定理求极限
有时候当看到所求得题目中出现了 的项,可以考虑使用拉格朗日中值定理,或者说是通过简单的变换就可以使用拉格朗日中值定理使用条件的比如
,这样会大大减少计算过程
首先给出拉格朗日的定义:
拉格朗日(Lagrange)中值定理 若函数f满足如下条件:
1)f在闭区间[a,b]上连续;
2)f在开区间(a,b)上可导
则在(a,b)上至少存在一点
使得
解题思路
1、首先确定要使用中值定理的项
2、用 进行替换
3.用夹逼定理求出的值,得出答案
例题1、求极限
分析:很快可以看出是符合拉格朗日中值定理条件的,然后得到区间
,将
开导得到
于是有
因为 所以有
解:利用Lagrange中值定理
例题2、
解:
tips:正无穷大: +\infty
负无穷大: -\infty
2、使用施笃兹定理求极限
当我们遇到、
两种形式的极限,当常规的方法无法进行运算时,可以看看是否满足施笃兹定理使用的条件,使用施笃兹定理可以快速得到答案
首先给出施笃兹的定义:
(1)
型 设数列{
}{
}满足:
1){
}严格单调递增;
2)
;
3)
(其中L可以为有限实数、
、
)
则
(2)
型 设数列{
}{
}满足:
1){
}严格单调递减趋于0;
2)
3)
(其中L可以为有限实数、
、
)
则
例3、
分析:很明显当n趋于时,分子是一个单调递增的数列,分母趋于无穷,满足施笃兹定理(1)的要求,所有求出L即为原式的极限
解:
3、利用泰勒公式
大部分的题目没有办法来进行化简都可以强行采取泰勒展开式进行计算
列出了常用的几项
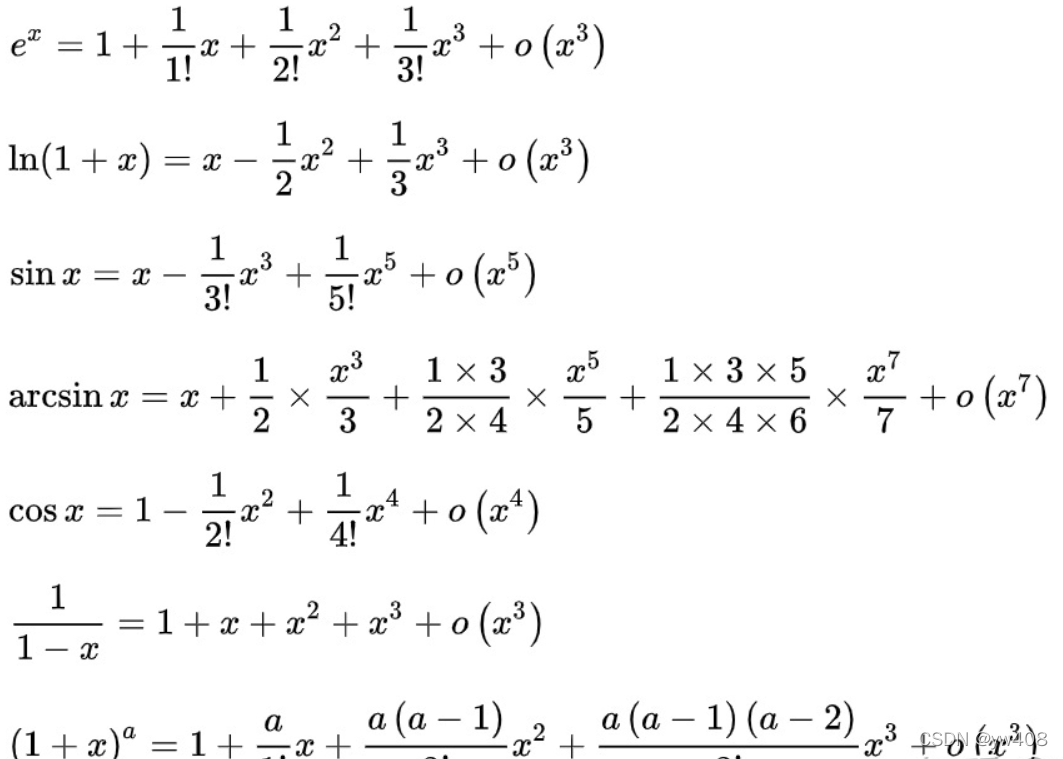
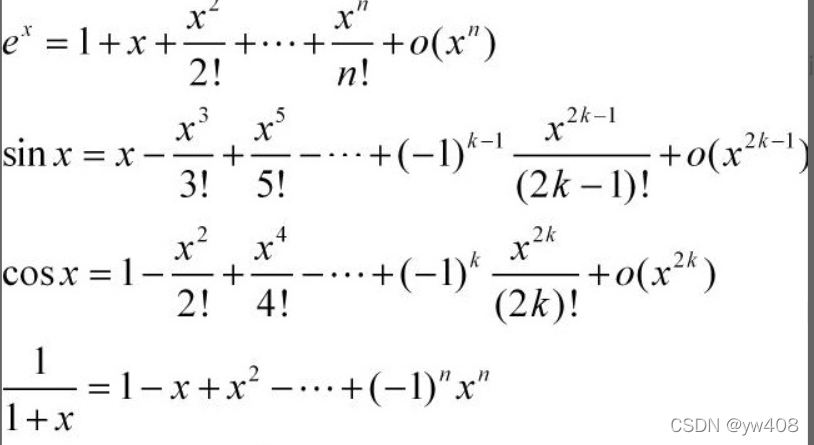





















 13万+
13万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










