目录
题目
作者: 冯向阳时间限制: 1S章节: 课程设计
问题描述 :
在使用图的邻接矩阵ADT的基础上,设计Dijkstra算法,用以解决单源最短路径问题,并以文本形式输出从源点到其余各个顶点的路径以及路径长度。将此算法加入到邻接矩阵ADT中,在邻接矩阵ADT中提供一个公有的成员函数Dijkstra。
提示:
(1)单源最短路径问题:已知有向带权图(简称有向网)G=(V,E),找出从某个源点s∈V到V中其余各顶点的最短路径。限定权值均为正整数。
(2)目的: 设一有向图G=(V, E),已知各边的权值,以某指定点v0为源点,求从v0到图的其余各点的最短路径。限定各边上的权值大于或等于0。应按路径“长度” 递增的次序,逐步产生最短路径。
(3)Dijkstra算法的基本步骤:设V0是起始源点,U = 已求得最短路径终点集合。V-U = 未确定最短路径的顶点的集合,初始时 U ={V0}。
1)“长度”最短的最短路径是边数为1的长度最小的路径。
2)下一条“长度”最短的路径:
① Vi ∈ V - U ,先求出V0 到Vi 中间只经 U 中结点的最短路径;
② 上述最短路径中长度最小者即为下一条长度最短的路径;
③ 将所求最短路径的终点加入U 中;
3)重复2)直到求出所有的最短路径。(4)实现方法:
1)图用带权邻接矩阵存储ad[][];
2)数组dist[]存放当前找到的从源点V0到每个终点的最短路径长度,其初态为图中直接路径权值;
3)数组pre[]表示从V0到各终点的最短路径上,此顶点的前一顶点的序号;若从V0到某终点无路径,则用-1作为其前一顶点的序号。参考函数原型:
(1)//Dijkstra算法(成员函数)
template<class TypeOfVer, class TypeOfEdge>
bool adjmatrix_graph<TypeOfVer, TypeOfEdge>::Dijkstra( int u, TypeOfEdge *dist, int *pre); // u:源点的位序(2)辅助函数
//最短路径输出(用户函数)
template<class TypeOfVer, class TypeOfEdge>
void searchPath(TypeOfVer *ver, int *prev, TypeOfEdge *dist, int v, int u); // ver:输入的顶点集 v:源点的位序 u:终点的位序
输入说明 :
第一行:图的类型
第二行:顶点数
第三行:顶点集
第四行:无边标记
第五行:边数
第六行:边集
第七行:权集
第八行:源点位序
输出说明 :
第一行:顶点集
空行
第二行:图的邻接矩阵
空行
第三行:dist数组的初值
第四行:pre数组的初值
空行
第五行:dist数组的值
第六行:pre数组的值
空行
第七行:源点到其余各顶点的最短路径及最短路径长度(输出格式参见测试数据)
输入范例
DN
7
V1 V2 V3 V4 V5 V6 V7
99
10
0 1
0 2
0 4
0 6
1 5
1 6
2 3
3 4
4 5
5 6
13 8 30 32 9 7 5 6 2 17
0输出范例
V1 V2 V3 V4 V5 V6 V7
99 13 8 99 30 99 32
99 99 99 99 99 9 7
99 99 99 5 99 99 99
99 99 99 99 6 99 99
99 99 99 99 99 2 99
99 99 99 99 99 99 17
99 99 99 99 99 99 990 13 8 99 30 99 32
-1 0 0 -1 0 -1 00 13 8 13 19 21 20
-1 0 0 2 3 4 1<(0,V1),(1,V2)>,13
<(0,V1),(2,V3)>,8
<(0,V1),(2,V3),(3,V4)>,13
<(0,V1),(2,V3),(3,V4),(4,V5)>,19
<(0,V1),(2,V3),(3,V4),(4,V5),(5,V6)>,21
<(0,V1),(1,V2),(6,V7)>,20
题目分析
解答
代码
完整代码呈现
#include "bits/stdc++.h"
using namespace std;
#define MvInt 32767
#define MVNum 101
#define VerTexType string
#define WeightType int
int flag,source;
struct AMGraph{
VerTexType ver[MVNum];
WeightType wei[MVNum][MVNum];
int arcnum,vernum;
};
void CreateDN(AMGraph &amGraph){
int vnum,anum;
vector<pair<int,int> > arc;
cin>>vnum;
amGraph.vernum=vnum;
for(int i=0;i<vnum;i++){
cin>>amGraph.ver[i];
}
cin>>flag;
for(int i=0;i<amGraph.vernum;i++){
for(int j=0;j<amGraph.vernum;j++){
amGraph.wei[i][j]=flag;
}
}
cin>>anum;
amGraph.arcnum=anum;
int st,en;
for(int i=0;i<anum;i++){
cin>>st>>en;
arc.emplace_back(make_pair(st,en));
}
for(int i=0;i<anum;i++){
cin>>amGraph.wei[arc.at(i).first][arc.at(i).second];
}
cin>>source;
for(int i=0;i<vnum;i++){
if(i!=vnum-1)
cout<<amGraph.ver[i]<<" ";
else
cout<<amGraph.ver[i];
}
cout<<endl<<endl;
for(int i=0;i<amGraph.vernum;i++){
for(int j=0;j<amGraph.vernum;j++){
cout<<amGraph.wei[i][j]<<" ";
}
cout<<endl;
}
cout<<endl;
}
void Print(int xu,AMGraph &amGraph,int pre[],bool fl=0){
if(xu==source)
{
cout<<"("<<xu<<","<<amGraph.ver[xu]<<")"<<",";
return;
}
Print(pre[xu],amGraph,pre,0);
cout<<"("<<xu<<","<<amGraph.ver[xu]<<")";
if(fl==0)
cout<<",";
}
void Dijkstra(AMGraph &amGraph){
int dist[MVNum],pre[MVNum],s[MVNum]={0};
//此处s数组用来记载是否这个顶点已经由源点通过最短路径到达过
for(int i=0;i<amGraph.vernum;i++){
dist[i]=amGraph.wei[source][i];
if(dist[i]&&dist[i]!=flag)
pre[i]=source;
else pre[i]=-1;
}
pre[source]=-1;//源点的前一个点自然为零
dist[source]=0;
for(int i=0;i<amGraph.vernum;i++){
cout<<dist[i]<<" ";
}
cout<<endl;
for(int i=0;i<amGraph.vernum;i++) {
cout<<pre[i]<<" ";
}
cout<<endl<<endl;
s[source]=1;
for(int i=0;i<amGraph.vernum;i++){
int mixLong=MvInt;
int x=0;
for(int j=1;j<amGraph.vernum;j++){
//要让从源点通向这个点的路及没有被访问过
//还要这条路是源点周边存在的路径的最短路径
if(!s[j]&&dist[j]<mixLong){
mixLong=dist[j];
x=j;
}
}
s[x]=1;
for (int j = 0; j < amGraph.vernum; j++) {
if (!s[j] && (dist[x] + amGraph.wei[x][j] < dist[j])) {
dist[j]= dist[x] + amGraph.wei[x][j];
pre[j]=x;
}
}
}
for(int i=0;i<amGraph.vernum;i++){
cout<<dist[i]<<" ";
}
cout<<endl;
for(int i=0;i<amGraph.vernum;i++){
cout<<pre[i]<<" ";
}
cout<<endl<<endl;
for(int i=0;i<amGraph.vernum;i++){
if(i==source)
continue;
cout<<"<";
bool fl=1;
Print(i,amGraph,pre,fl);
cout<<">"<<","<<dist[i];
if(i!=amGraph.vernum-1)
cout<<endl;
}
}
int main(){
string string1;
cin>>string1;
AMGraph amGraph;
CreateDN(amGraph);
Dijkstra(amGraph);
return 0;
}具体代码解读
首先按照题目要求构造一个图,下面是基本代码,不做赘述
#include "bits/stdc++.h"
using namespace std;
#define MvInt 32767
#define MVNum 101
#define VerTexType string
#define WeightType int
int flag,source;
struct AMGraph{
VerTexType ver[MVNum];
WeightType wei[MVNum][MVNum];
int arcnum,vernum;
};
void CreateDN(AMGraph &amGraph){
int vnum,anum;
vector<pair<int,int> > arc;
cin>>vnum;
amGraph.vernum=vnum;
for(int i=0;i<vnum;i++){
cin>>amGraph.ver[i];
}
cin>>flag;
for(int i=0;i<amGraph.vernum;i++){
for(int j=0;j<amGraph.vernum;j++){
amGraph.wei[i][j]=flag;
}
}
cin>>anum;
amGraph.arcnum=anum;
int st,en;
for(int i=0;i<anum;i++){
cin>>st>>en;
arc.emplace_back(make_pair(st,en));
}
for(int i=0;i<anum;i++){
cin>>amGraph.wei[arc.at(i).first][arc.at(i).second];
}
cin>>source;
for(int i=0;i<vnum;i++){
if(i!=vnum-1)
cout<<amGraph.ver[i]<<" ";
else
cout<<amGraph.ver[i];
}
cout<<endl<<endl;
for(int i=0;i<amGraph.vernum;i++){
for(int j=0;j<amGraph.vernum;j++){
cout<<amGraph.wei[i][j]<<" ";
}
cout<<endl;
}
cout<<endl;
}
void Print(int xu,AMGraph &amGraph,int pre[],bool fl=0){
if(xu==source)
{
cout<<"("<<xu<<","<<amGraph.ver[xu]<<")"<<",";
return;
}
Print(pre[xu],amGraph,pre,0);
cout<<"("<<xu<<","<<amGraph.ver[xu]<<")";
if(fl==0)
cout<<",";
}其次是对于Dijkstra算法的基本操作,将源点直接到各个点的距离(包括通不过代表的99)全部记录,以及最浅显的初步pre记录输出
int dist[MVNum],pre[MVNum],s[MVNum]={0};
//此处s数组用来记载是否这个顶点已经由源点通过最短路径到达过
for(int i=0;i<amGraph.vernum;i++){
dist[i]=amGraph.wei[source][i];
if(dist[i]&&dist[i]!=flag)
pre[i]=source;
else pre[i]=-1;
}
pre[source]=-1;//源点的前一个点自然为零
dist[source]=0;
for(int i=0;i<amGraph.vernum;i++){
cout<<dist[i]<<" ";
}
cout<<endl;
for(int i=0;i<amGraph.vernum;i++) {
cout<<pre[i]<<" ";
}
cout<<endl<<endl;
代码详解与难点分析(可无)
关键是最短路径的生成部分,这一部分的思想是递归或者说递推,首先最简单的最短路径问题是由原点出发寻找周围路径中的最短路径的问题,而在找到之后的最短路径问题可以通过物理学中的矢量三角思想化简成为了第一部中那样子,具体过程如下: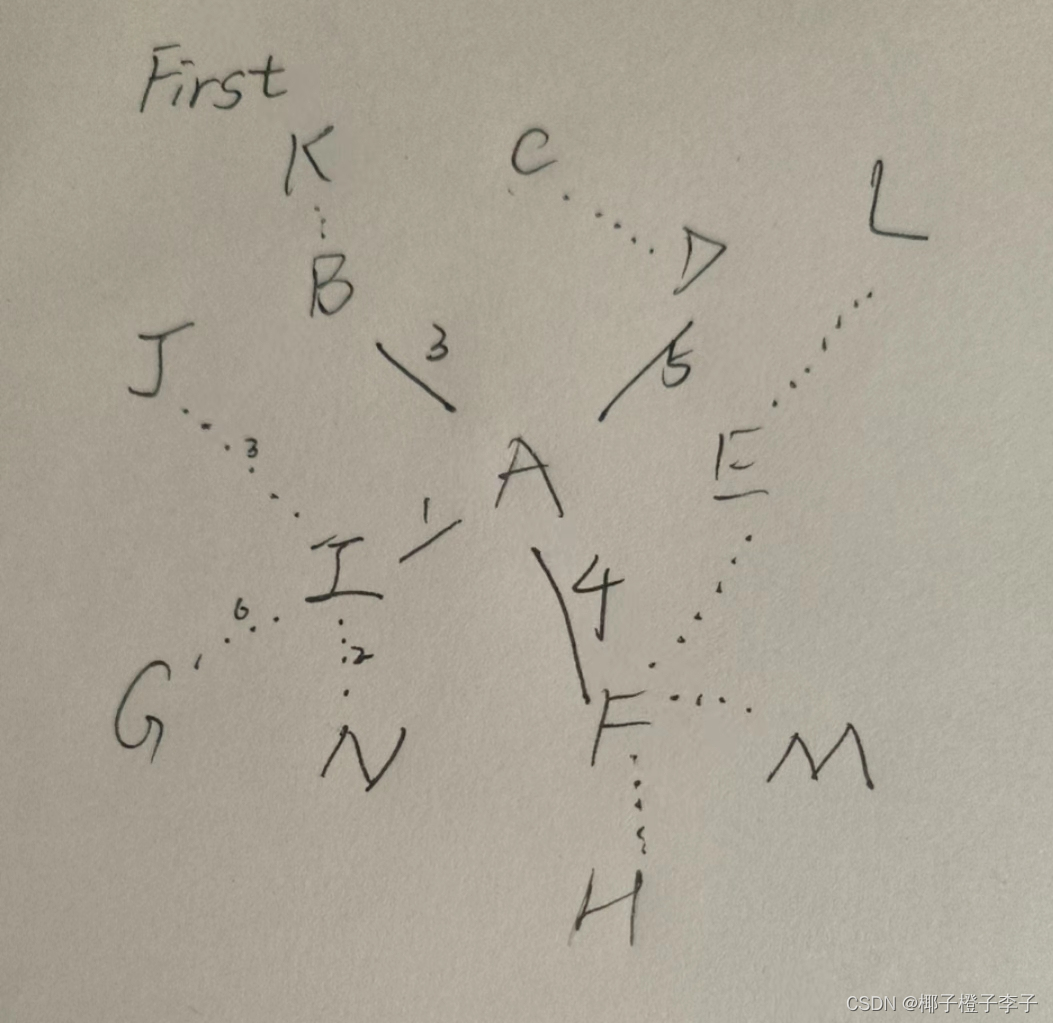
第一步 找到A周围所有直接与他相连的线,并找到权值最小的那个,将这条线记为已经是A到达那一个点(在这里是I点)的最短路径,并且在今后轮到找I点的最短路径时可以不必再找。
代码实现如下:
s[source]=1;
for(int i=0;i<amGraph.vernum;i++){
int mixLong=MvInt;
int x=0;
for(int j=1;j<amGraph.vernum;j++){
//要让从源点通向这个点的路及没有被访问过
//还要这条路是源点周边存在的路径的最短路径
if(!s[j]&&dist[j]<mixLong){
mixLong=dist[j];
x=j;
}
}
s[x]=1;//确定从源点到序号为x的点的最短路径已经找到第二步 找到I点周围所有相连的点:J G N并且利用矢量三角形原理与A点直接连接,如此可以将问题还原,仍然是找到A周围所有直接与他相连的线,并找到权值最小的那个,将这条线记为已经是A到达那一个点(此处为B点或N点)并且在今后轮到找B或N点的最短路径时可以不必再找。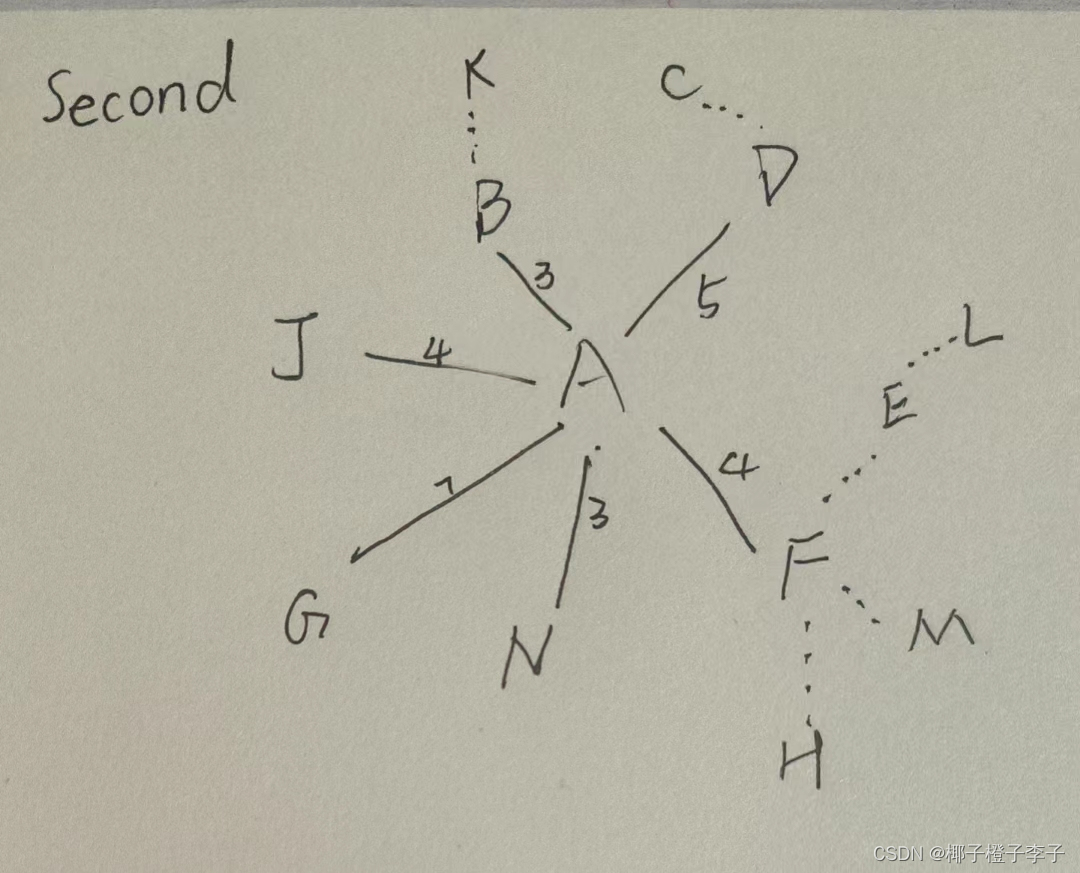
具体代码实现如下:
for (int j = 0; j < amGraph.vernum; j++) {
if (!s[j] && (dist[x] + amGraph.wei[x][j] < dist[j])) {
dist[j]= dist[x] + amGraph.wei[x][j];
pre[j]=x;
}
}
}类比可发现:
if (!s[j] && (dist[x] + amGraph.wei[x][j] < dist[j]))与if(!s[j]&&dist[j]<mixLong)这两个if语句本质的相同,从而可以发现这里的将问题转化为已经解决的问题的基本思想,也就是递归递推思想。
最后一个难点是按照格式输出
void Print(int xu,AMGraph &amGraph,int pre[],bool fl=0){
if(xu==source)
{
cout<<"("<<xu<<","<<amGraph.ver[xu]<<")"<<",";
return;
}
Print(pre[xu],amGraph,pre,0);
cout<<"("<<xu<<","<<amGraph.ver[xu]<<")";
if(fl==0)
cout<<",";
}有两点:第一点,他利用默认形参实现了只有第一次传入1使他不回输出逗号,其余全部因为默认形参而输出逗号。
第二点:他利用递推思想,不断回溯,每次输出一个点信息,最终输出最后点信息。
分析
算法的性能分析
这个人很懒,什么性能都没有分析……




















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








