Coin Change

最新推荐文章于 2024-10-09 18:52:46 发布

原创最新推荐文章于 2024-10-09 18:52:46 发布 · 122 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法

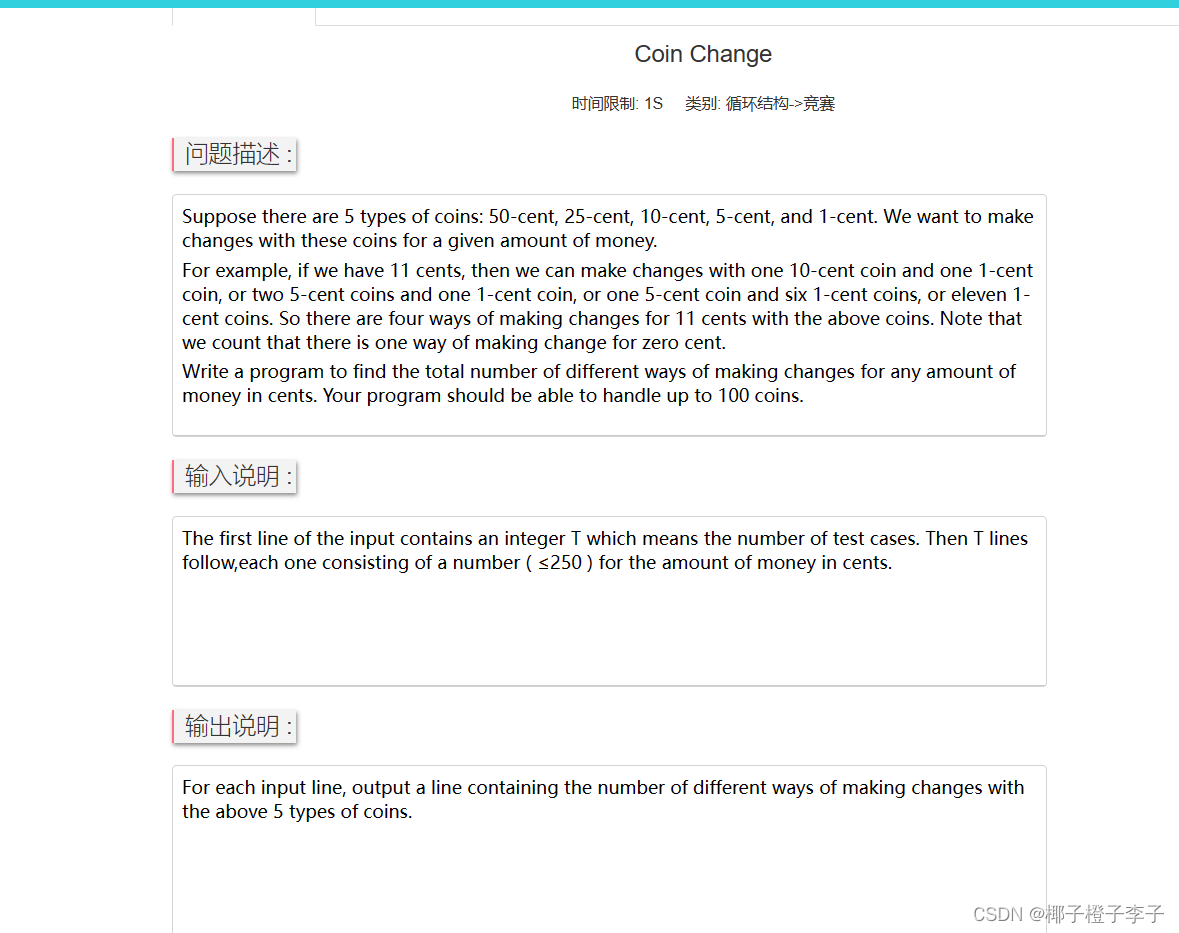
题目

输入范例

5
1
100
200
250
198

输出范例

1
292
2061
3830
1886

题目分析

他这里有两个限制，一个是和最大不超过250，一个是硬币数目不超过100个，这个大大降低了此题的难度与对于算法时间复杂度的要求，所以我的思路写成的也过了，接下来将介绍两种思路以及两种思路下的代码

解答

我的思路

关键函数，其中mon代表要达到的数额，cot代表可行方案数目，index等会说，n表示硬币数目

int coin[6]={50,25,10,5,1};
void solve(int mon,int &cot,int index=0,int n=0){
    int i;
    for(i=index;i<5;i++){
        if(mon>=coin[i])
            break;
    }
    if(coin[i]==1||i==5)
    {//发现mon比5还小，直接用最小面值1全部表示
//又或者，mon在上一个函数递归中已经被减尽，那么这里只需要检验一下是否n<=100就可以增加方案数目cot了
        n+=mon;
        if(n<=100)
            cot++;
    }
    else for(int j=mon/coin[i];j>=0;j--){
//j代表此时要拿出coin[i]大小面值的硬币数目，由大至小依次遍历，同时为了防止无限循环
//将index改为i+1，同时硬币数目也因为已经拿出来了j个coin[i]大小面值的硬币而变成了n+j；
        solve(mon-j*coin[i],cot,i+1,n+j);
    }
}

代码

#include "bits/stdc++.h"
using namespace std;
int coin[6]={50,25,10,5,1};
void solve(int mon,int &cot,int index=0,int n=0){
    int i;
    for(i=index;i<5;i++){
        if(mon>=coin[i])
            break;
    }
    if(coin[i]==1||i==5)
    {//发现mon比5还小，直接用最小面值1全部表示
//又或者，mon在上一个函数递归中已经被减尽，那么这里只需要检验一下是否n<=100就可以增加方案数目cot了
        n+=mon;
        if(n<=100)
            cot++;
    }
    else for(int j=mon/coin[i];j>=0;j--){
//j代表此时要拿出coin[i]大小面值的硬币数目，由大至小依次遍历，同时为了防止无限循环
//将index改为i+1，同时硬币数目也因为已经拿出来了j个coin[i]大小面值的硬币而变成了n+j；
        solve(mon-j*coin[i],cot,i+1,n+j);
    }
}
int main(){
    int num,cot,mon;
    cin>>num;
    for(int i=0;i<num;i++){
        cot=0;
        cin>>mon;
        solve(mon,cot);
        cout<<cot<<endl;
    }
    return 0;
}

代码详解与难点分析（可无）

全在关键函数注释中

分析

好处就是思路清晰，先解决大块硬币，在解决小块，难点就是在递归的同时考虑到同一个数额的不同表示（10表示为1个10或者2个5或者10个1）然后解决。

算法的性能分析

递归函数当数额比较大的时候时间成本会大大增加，不建议使用。

zqw的思路

用n个硬币（面值不同）凑出数额为m的方案有x种，那么如果减少一枚硬币，用n-1枚硬币就有且仅有可能凑出m-1,m-5,m-10,m-25,m-50这五种数目的金额，并将凑出这五种数目的金额的方案分别记为x1,x2,x3,x4,x5那么很自然x=x1+x2+x3+x4+x5;如果把x1-5中任意一个放到x的位置同理，由此可以回溯到x等于1的时候，n也=1，m=1/5/10/25/50;

代码

其中关键的一行语句

mon[k][j]+=mon[k-1][j-cent[i]];

表示用k个硬币凑出j元的方案数目=用k-1个硬币凑出对应五种可能（j-1/j-5/j-10/j-25/j-50)的方案数目总合，这里因为要加五种可能，所以第一个for循环就变得好理解了，但是由于这道题回溯的特性是知道所有目标值以下任意金额对应的硬币数和方案数，所以他需要遍历金额从1到n，硬币数从1到100的所有对应的mon[k][j]的值，最后从中找到自己要的，加起来。

 #include <bits/stdc++.h>
using namespace std;
int cent[5]={1,5,10,25,50};
int mon[110][260]={0};
//二维数组第一个下标表示硬币数目，第二个下标表示要达到的金额。
//而mon[k][j]表示用k个硬币凑出j元的方案数目。
int main()
{
    int n;
    while(cin>>n)
    {
        memset(mon,0,sizeof(mon));
        mon[0][0]=1;//边界初始化
        int sum=0;
        for(int i=0;i<5;i++)
            for(int k=1;k<=100;k++)
                for(int j=cent[i];j<=n;j++)
                    mon[k][j]+=mon[k-1][j-cent[i]];
        for(int i=1;i<=100;i++) sum+=mon[i][n];
        cout<<sum<<endl;
    }

    return 0;
}