次表面散射 | Vol.3 使用单通道方差引导自适应重要性采样来实现次表面实时渲染

专题介绍

在实时渲染和离线渲染领域，对场景模型表面以及空间介质的精细化建模是增加场景真实感的重要手段。计算机图形学领域的许多科研工作者设计出一系列复杂精巧的技术理论，模拟出光线从宏观世界到微观粒子的变化规律。本期专题精选了近年来关于微表面模型、次表面散射模型等相关前沿工作，为读者解读其中的关键技术。

一、研究背景

1.1 次表面散射

SDF方程。次表面散射是实时绘制中一个重要的特性，可用于模拟皮肤、玉石、蜡、大理石、植物等半透材质。当下次表面散射主要还是用在人脸绘制上，较早的时候是当做participating media来渲染，例如volumetric path tracing之类的做法，这样当然非常慢，特别对于皮肤之类的散射系数很高的物体，path tracing特别难收敛，在diffusion profile提出之后，次表面材质的绘制才变得高效，往后的很大部分工作是基于diffusion profile的拟合上。

1.2 BSSRDF

除了把次表面材质当做volumetric来处理以外，另一类方法就是通过BSSRDF来描述。含BSSRDF的rendering equation如下：

BSSRDF为：

其中1/π是归一化系数，Ft是菲涅尔项，Rd就是我们所说Diffuse profile，是一个关于入射点和出射点距离的函数，这样就把体绘制中在体内部的复杂的散射简化为入射点和出射点之间的能量传输。这里的Rd只和距离相关，这是因为只考虑多散射的情况，多散射在散射介质中趋向于各项同性，因此和方向无关。BRDF本质上是BSSRDF的近似，如果假设入射和出射是同一点的话就退化成了BRDF。Rd乘2πr的积分就等于物体的albedo。对Rd的拟合有Dipole、高斯核、可分离的kernel等等方法。

1.3 TAA

另外这篇文章还涉及了TAA。Temporal anti-aliasing (TAA) [Karis 2014] 通过累计历史若干帧的结果达到超采样的目的，但因为显然不能直接存很多历史帧，所以用exponential moving average来做。S是当前值，α是blending的权重。λ是个context，因为取历史结果以及决定最终的权重系数的时候，通常还要考虑velocity、颜色差异之类的。Pi是一个jitter后的位置，jitter的offset由f(i)决定。

μi is the estimated value at pi

C(xi,Λ) is the clamped history context term

S(pi) is the current-frame shading term

M(α0,Λ) is the weight update function

N(xi,f(i)) is the neighbor sampling function

二、主要贡献

这篇文章最主要的贡献在于：引入adaptive sampling，不使用固定的一个kernel做卷积，而是每个像素用不同的采样数来做importance sampling，让采样数高的像素尽可能地集中在variance大的地方，而且他们的整体的算法还比较简单，而且比较general，也许也可以应用在除了次表面以外的其他算法上。

三、方法

3.1 目标

这篇文章的主要目的，就是要在实时的次表面绘制中使用蒙特卡洛方法，而且需要是adaptive的，两个需要解决的问题：如何得知一个尽可能小的采样数，知道采样数后，如何做importance sampling，分配具体的sample。

3.2 确定最小采样数

首先是采样数的估计，我们希望采样数自适应地在需要的区域较多，例如说light gradient大的地方，在不需要的区域尽可能少，比如说阴影区域。因此需要一个用于估计采样数的metric，这个metric由当前帧i的采样数n、前i-1帧的均值方差和一个预设的我们所期望的较小的方差σ0得到。β是根据前一帧的采样数设定的一个采样数的下限，避免采样数过少：

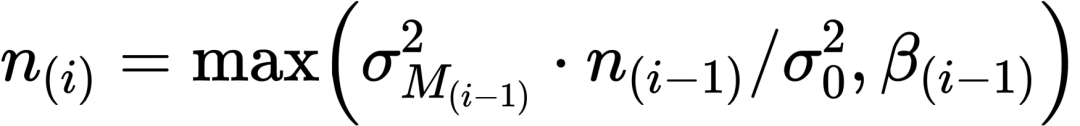
我们并不知道每个像素具体的分布情况，为了计算均值方差，根据中心极限定理，样本均值会趋向于服从正态分布，这样均值方差可以通过总体方差得到：

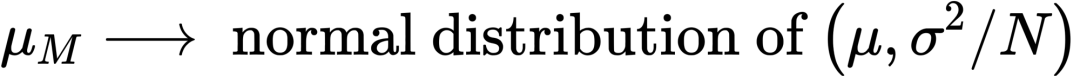
所以接下来借鉴TAA的思想，把这个基础的准则变成带有temporal accumulation。首先要证明一下，在TAA中exponential moving average是如何收敛到均值的：

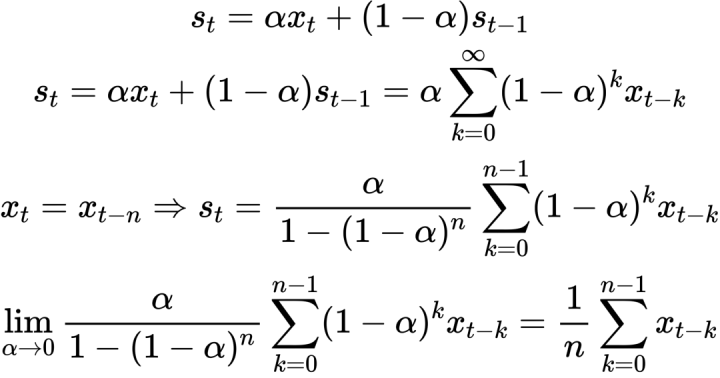
既然如此，我们对于每一帧的采样数也和TAA一样做exponential moving average，作为历史值的一项记录下来。前面证明了当α很小的时候，EMA的结果能近似地作为均值，于是我们得到了每个像素，前i帧的采样数的均值：

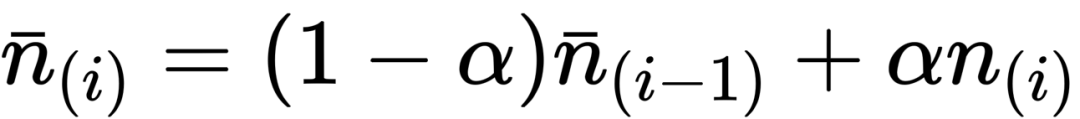
类似的，我们对总体的方差也做exponential moving average，得到下式，也就是每个像素前i帧的总体方差：

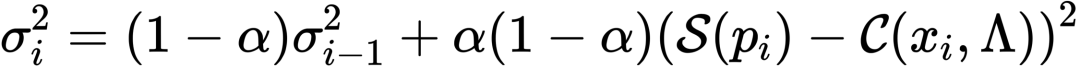
有了上面的结果后，我们把基本的metric改为累加的形式，考虑连续的k帧，则估计的第i帧的采样数最终变为下式，所有的量都是已知的：

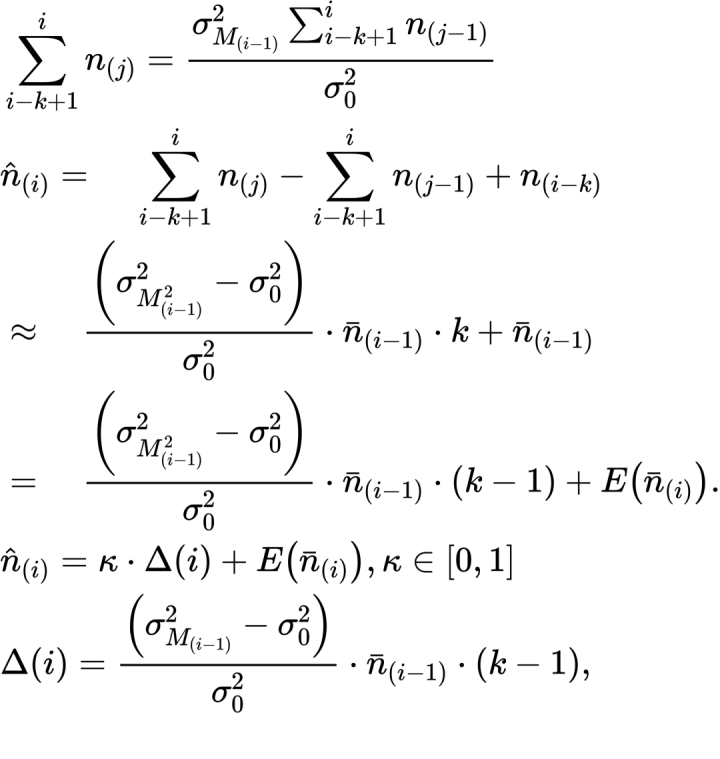
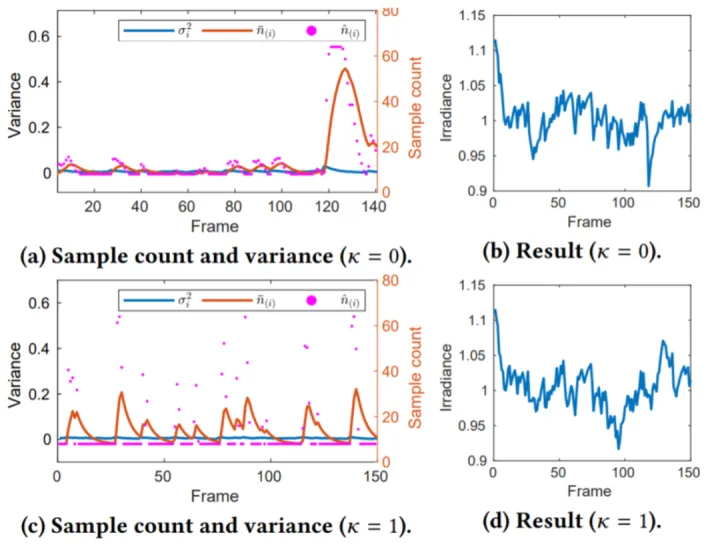
这就是最终的adaptive metric，还加了k这个控制系数来决定采样数变化的幅度。文章用一个circle senario来演示这个metric：把模型简化为采一个半径为0.5的圆的irradiance ，圆内的irradiance是4/π，圆外是0，圆的面积是π/4，如果采样结果足够理想，结果应该接近1。K是一个控制系数，可以看到k取0的时候，采样数会缓慢变化来降低方差，k取1的时候，采样数会跳变到一个很大的值，然后持续几帧后到一个稳定值。然后结果都是维持在1左右：

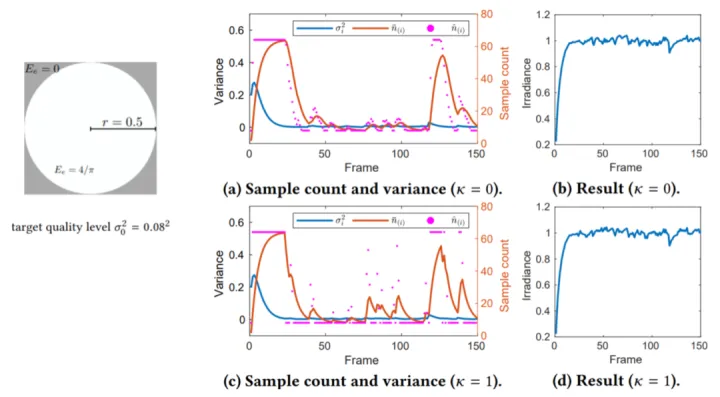
但在最开始的时候的几十帧内采样数会在一个较高的值，这种情况会普遍存在于一个次表面物体在上一帧被遮挡，但这一帧不被遮挡的情景（Disocclusion）。因此针对Disocclusion的情况，对blending weight以及方差的选择做出修改，当没有历史数据的时候，blending的时候只取当前的颜色S，方差取预设的最小方差：

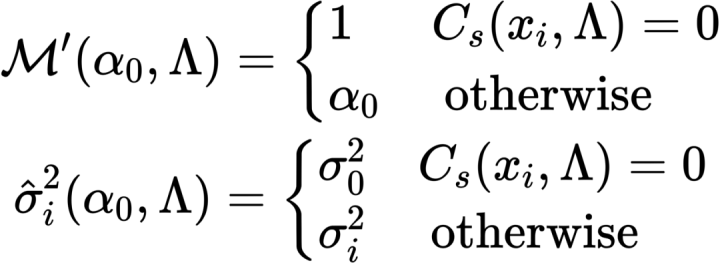
在同样的circle senario下，最开始的sample count的peak消失了：

3.3 重要性采样

评估完最小的采样数之后，接下来就是怎么做重要性采样。主要是沿用了15年迪士尼的diffuse profile的拟合，拟合成了一个非常简单的解析式，叫做normalized diffuse：

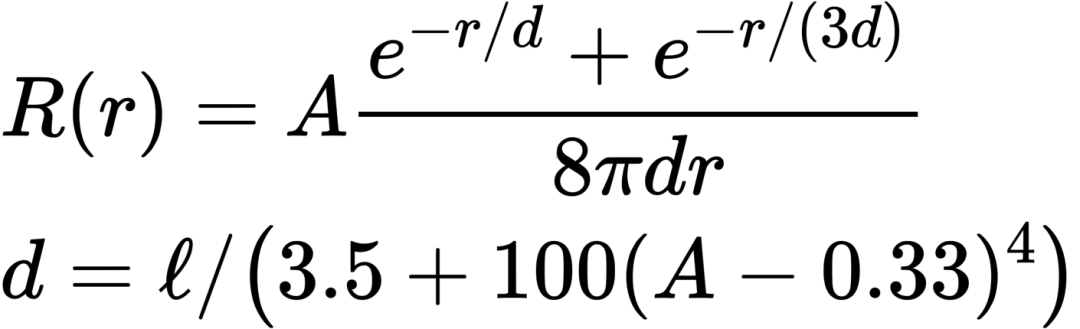
相比于dipole或者预计算好的kernel有三个好处：

1. 由于是直接从MC结果拟合，意味着包含所有的散射项，dipole则只包含了multiscattering。

2. 参数更加友好，dipole模型所需的参数α’需要根据artist指定的albedo解出来，而对于normalized diffuse，可以直接指定albedo和平均自由程。

3. CDF具有解析形式，因此可以用于importance sampling：

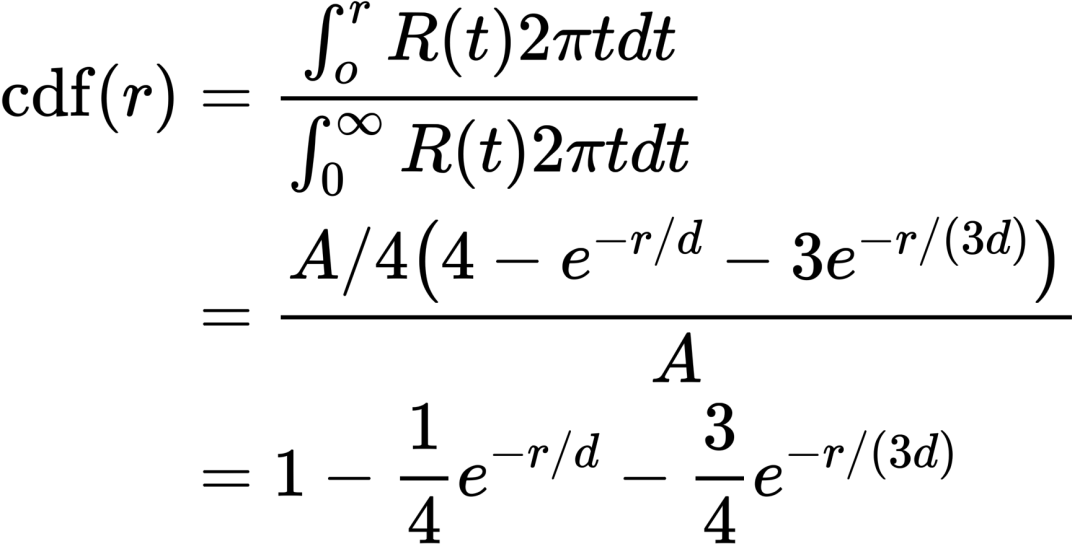
但是没有解析的反函数，CDF有两个指数部分，原文作者建议用MIS，或者用少量的牛顿迭代，或者用LUT。这篇文章给了一个对CDF的拟合式，取c=2.5715得到一个比较小的百分误差：

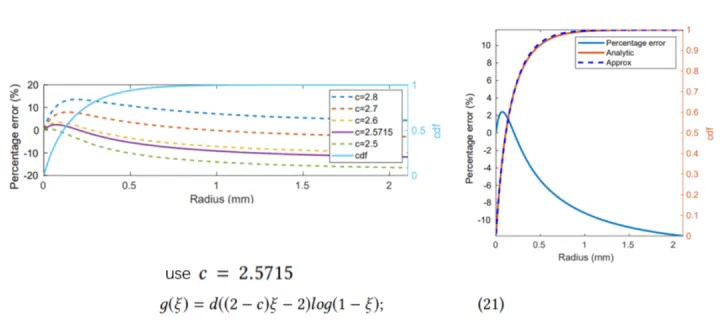
最后就可以得到常规的重要性采样的表达式：

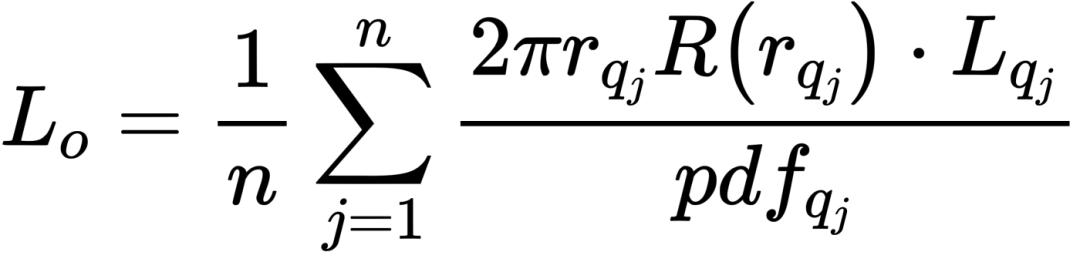
3.4 整体流程

这张图概括了整体的流程：

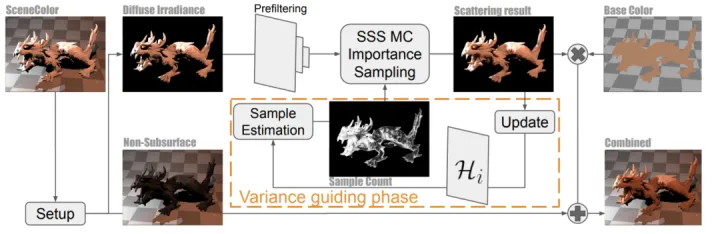
一开始做了prefilter，其实就是对diffuse做mip，这样一方面pdf小的地方采更高的mip能够达到降噪的效果，另一方面可以增加cache hit，因为做了mip后采样会变得更加coherent。另外用双边滤波来解决不同的次表面材质边缘的bleeding。

四、结果

4.1 和 ground truth的对比

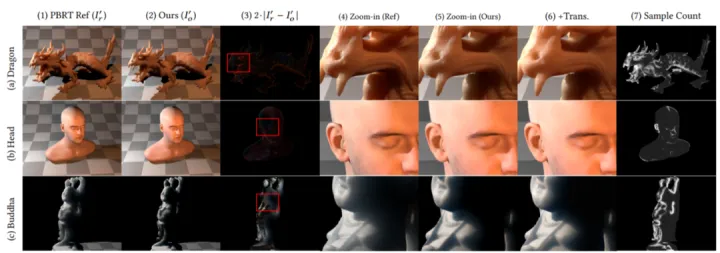
4.2 和separable sss的对比

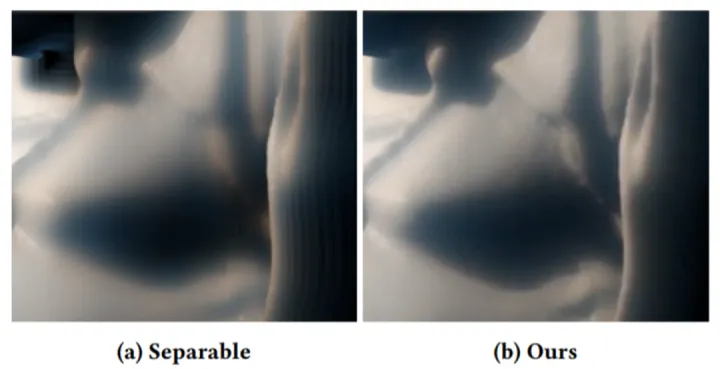
4.3 耗时（等PSNR）

4.4 质量（等时间）

4.5 各种方法的比较

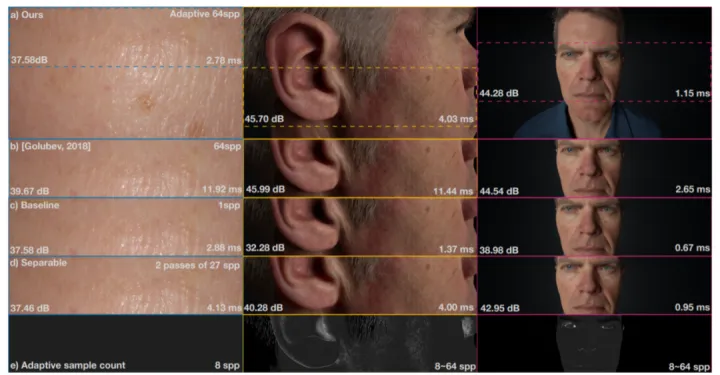
五、不足

1.只在较为平坦的区域有较大的加速效果。

2.对variance 的评估不够准确，导致部分区域使用了比实际所需的更多的采样数。

3.整体上是一种估计，所得的采样数是有偏的。

*本文由 Shiro小白 同学辛苦整理，如有错漏之处，敬请指正。

[1] Xie T, Olano M, Karis B, et al. Real-time subsurface scattering with single pass variance-guided adaptive importance sampling[J]. Proceedings of the ACM on Computer Graphics and Interactive Techniques, 2020, 3(1): 1-21.