微表面模型 | Vol.1 基于微表面模型的法线贴图

专题介绍

在实时渲染和离线渲染领域，对场景模型表面以及空间介质的精细化建模是增加场景真实感的重要手段。计算机图形学领域的许多科研工作者设计出一系列复杂精巧的技术理论，模拟出光线从宏观世界到微观粒子的变化规律。本期专题精选了近年来关于微表面模型、次表面散射模型等相关前沿工作，为读者解读其中的关键技术。

01 研究背景

法线贴图（Normal Map）是凹凸贴图（Bump Map）的一种实现方式，常常用于在低解析度的模型，伪装出出高解析度的模型细节表现。法线贴图的每个像素储存了法线，红色、绿色、蓝色通道分别对应了X、Y、Z的方向。

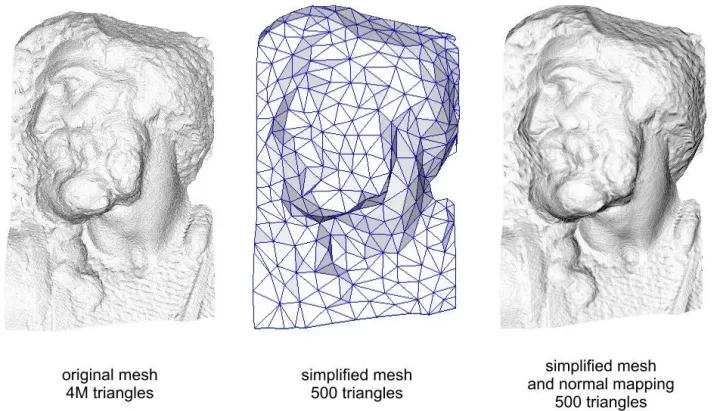
图片来源“learnopengl-normal mapping”

如上图所示[1]，左侧是高解析度的模型，中间是简化过的模型，通过法线贴图，我们可以得到右侧的效果。

微表面模型（Microfacet Model）假设物体的表面，由很多凹凸不平的微小镜面组成。这些具有不同大小、方向的微表面在对入射光线进行反射时产生了不同的反射效果，从而使得人眼能观察到不同的材质属性。在人眼观察的时候，只有入射方向和出射方向的平均方向会参与反射的计算，如下图所示。

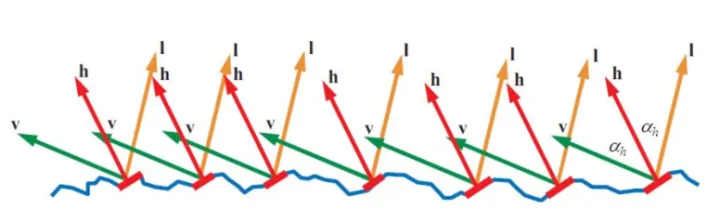
02 法线贴图存在的问题

在实时绘制中，法线贴图可以比较好的模拟高解析度的效果。但是，对于数学上要求更为严格的离线绘制而言，法线贴图存在如下的问题：

1.光路的不对称性

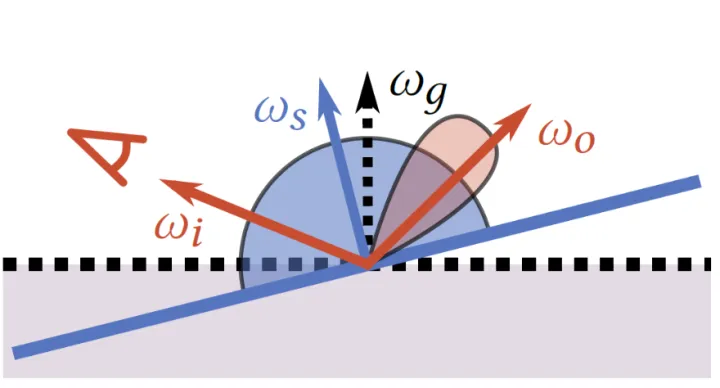
如上图所示，我们可以看到BRDF形状的法向偏转为 ws 。但是，表面本身没有发生变化，光线投影的Cosine项应该使用同 wg 的夹角的余弦值，所以需要对BRDF函数进行校正：

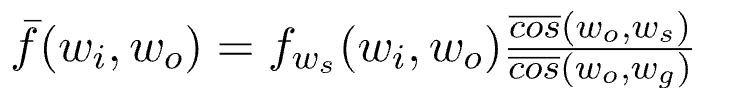
那么，对于正向的追踪过程：

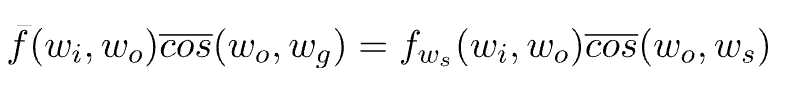
对于逆向的追踪过程：

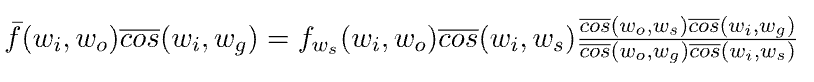
可以看到，正向和逆向的两个追踪过程的BRDF结果不对称。并且， cos~(wo,ws)cos~(wi,wg)cos~(wo,wg)cos~(wi,ws) 在计算过程中，会带来的很大的方差，具体的信息可以参考Mitsuba的提交记录。

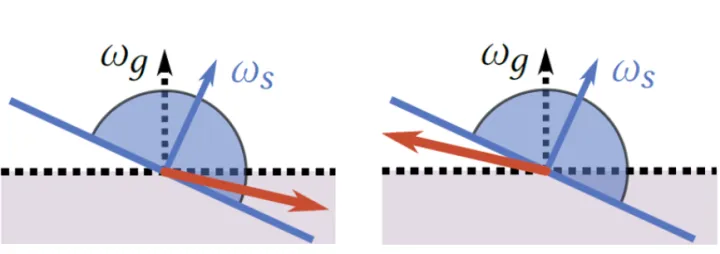
2.黑色的边缘

只考虑最原始的法线贴图实现，我们会发现当法向偏转之后，会造成下图所示的两种问题。