利用梯度下降法和牛顿法求解问题--哈工大人工智能数学基础LAB3

1. 实验内容或者文献情况介绍

实验内容为实现用梯度下降求解二项逻辑回归模型，并用牛顿法求解一个高维的非线性问题。

在这次实验中，我编写了算法并取了实例进行求解。在梯度下降法求解逻辑回归问题时使用的模型数据是以前的100位申请人的两项考试成绩和是否录取情况（1/0），用它作为逻辑回归的训练集，建立一个分类模型，根据考试成绩估计入学概率。而牛顿法求解高维的线性问题时我使用了一个问题实例，也就是下式，并给出 , 要求求解。

 

2. 算法简介及其实现细节

梯度下降和牛顿法的推导均与泰勒公式有关，所以先介绍泰勒展开公式，其基本形式如下：

 

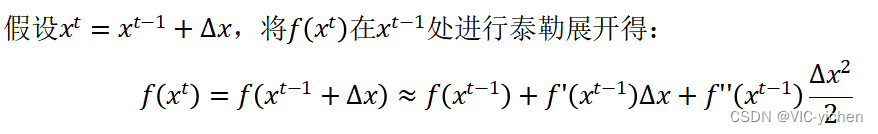
上面这个迭代形式将应用到下面的梯度下降和牛顿法中。

2.1 梯度下降法原理简介

首先我们知道梯度是一个向量，梯度的方向与最大方向导数的方向一致，梯度的模为方向导数的最大值；梯度是一个向量组合，反映了多维图形中变化速率最快的方向。而梯度下降法就是沿着负梯度方向依次迭代、优化。

以下山为例，我们研究从山顶到山脚有无数条下山路径如何选择最佳路径。

梯度下降法的思想如下：以当前的位置（山顶）为起点，寻找坡度最大的一步为接下来要走的第一步；这一步走完后，继续以当前位置为起点，寻找坡度最大的一步为接下来要走的第二步…以此类推，直到从山顶走到山脚为止。

而这个实例的数学依据如下。

由于在空间变量的某一点处，函数沿梯度方向具有最大的变化率，所以在优化目标的时候，自然是沿着负梯度的方向去减小函数值。

迭代公式： 

2.1.1 逻辑回归

 

 

2.1.2 损失函数

实验一我们做线性回归模型时，给出了线性回归的代价函数的形式（误差平方和函数），但是并不能应用到逻辑回归中，这是因为LR的假设函数的外层函数是Sigmoid函数，Sigmoid函数是一个复杂的非线性函数，这就使得我们将逻辑回归的假设函数带入上式时，得到的是一个非凸函数。因此，此处我们需要重新考虑损失函数。

在逻辑回归中，我们最常用的损失函数为对数损失函数，对数损失函数可以为LR提供一个凸的代价函数，有利于使用梯度下降对参数求解。其图像在0-1区间上当z=1时，函数值为0，而z=0时，函数值为无穷大。这就可以和代价函数联系起来，在预测分类中当算法预测正确其代价函数应该为0；当预测错误就应该用一个很大代价（无穷大）来惩罚我们的学习算法，使其不要轻易预测错误。

因此重新定义逻辑回归的代价函数如下：

 

损失函数的求解为：

 

由此我们回到梯度下降法来解题。

第一步，将我们的 初始化为[[0][0][0]]。

第二步，对于给定的步长和此时的梯度gradient。梯度计算公式如下：

 

更新我们的。然后计算此时对应的梯度更新gradient。

第三步，重复第二步一定次数

第四步，返回，即为回归的参数。

2.2 梯度下降法求解实现细节

对于逻辑回归来说，梯度下降法遇到了一个问题，那就是步长和迭代次数的取值，如果步长过小，损失函数将收敛的非常慢，迭代次数达到40万时才勉强收敛，但如果步长过大，又会导致过大的步长使得准确率下降。因此经过尝试最终确定了收敛效果最好的步长为约0.005，迭代次数约30万。

在此处我将建立一个逻辑回归模型来预测一个学生是否被大学录取，即根据两次考试的结果来决定每个申请人的录取机会。将以前的申请人的历史数据作为逻辑回归的训练集。每一个训练数据包含两个考试的分数和录取决定（1/0）。数据存在tiduxiajiang文件夹中的Logi_Reg.txt中。

主要部分可以分为数据处理，建立分类器。而分类器的建立又分为以下几个要完成的模块：sigmoid映射到概率的函数；model返回预测结果值；cost根据参数计算损失；gradient 计算每个参数的梯度方向；descent进行参数更新；accuracy计算精度；以及sigmoid 函数。其中计算公式可见2.1。

其python代码如下：

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

import numpy.random

import time

def sigmoid(z):

    return 1 / (1 + np.exp(-z))

def model(X, theta):

    return sigmoid(np.dot(X, theta.T))

def cost(X, y, theta):

    left = np.multiply(-y, np.log(model(X, theta)))

    right = np.multiply(1 - y, np.log(1 - model(X, theta)))

    return np.sum(left - right) / (len(X))

def gradient(X, y, theta):

    grad = np.zeros(theta.shape)

    error = (model(X, theta) - y).ravel()

    for j in range(len(theta.ravel())):  # for each parmeter

        term = np.multiply(error, X[:, j])

        grad[0, j] = np.sum(term) / len(X)

    return grad

STOP_ITER = 0

STOP_COST = 1

STOP_GRAD = 2

def stopCriterion(type, value, threshold):

    # 设定三种不同的停止策略

    if type == STOP_ITER:  # 设定迭代次数

        return value > threshold

    elif type == STOP_COST:  # 根据损失值停止

        return abs(value[-1] - value[-2]) < threshold

    elif type == STOP_GRAD:  # 根据梯度变化停止

        return np.linalg.norm(value) < threshold

# 洗牌

def shuffleData(data):

    np.random.shuffle(data)

    cols = data.shape[1]

    X = data[:, 0:cols - 1]

    y = data[:, cols - 1:]

    return X, y

def descent(data, theta, batchSize, stopType, thresh, alpha):

    # 梯度下降求解

    init_time = time.time()

    i = 0  # 迭代次数

    k = 0  # batch

    X, y = shuffleData(data)

    grad = np.zeros(theta.shape)  # 计算的梯度

    costs = [cost(X, y, theta)]  # 损失值

    while True:

        grad = gradient(X[k:k + batchSize], y[k:k + batchSize], theta)

        k += batchSize  # 取batch数量个数据

        if k >= n:

            k = 0

            X, y = shuffleData(data)  # 重新洗牌

        theta = theta - alpha * grad  # 参数更新

        costs.append(cost(X, y, theta))  # 计算新的损失

        i += 1

        if stopType == STOP_ITER:

            value = i

        elif stopType == STOP_COST:

            value = costs

        elif stopType == STOP_GRAD:

            value = grad

        if stopCriterion(stopType, value, thresh): break

    return theta, i - 1, costs, grad, time.time() - init_time

def runExpe(data, theta, batchSize, stopType, thresh, alpha):

    # import pdb

    # pdb.set_trace()

    theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha)

    name = "Original" if (data[:, 1] > 2).sum() > 1 else "Scaled"

    name += " data - learning rate: {} - ".format(alpha)

    if batchSize == n:

        strDescType = "Gradient"  # 批量梯度下降

    elif batchSize == 1:

        strDescType = "Stochastic"  # 随机梯度下降

    else:

        strDescType = "Mini-batch ({})".format(batchSize)  # 小批量梯度下降

    name += strDescType + " descent - Stop: "

    if stopType == STOP_ITER:

        strStop = "{} iterations".format(thresh)

    elif stopType == STOP_COST:

        strStop = "costs change < {}".format(thresh)

    else:

        strStop = "gradient norm < {}".format(thresh)

    name += strStop

    print("***{}\nTheta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format(

        name, theta, iter, costs[-1], dur))

    fig, ax = plt.subplots(figsize=(12, 4))

    ax.plot(np.arange(len(costs)), costs, 'r')

    ax.set_xlabel('Iterations')

    ax.set_ylabel('Cost')

    ax.set_title(name.upper() + ' - Error vs. Iteration')

    return theta

path = 'C:\\Users\\Vic\\Desktop\\LogiReg_data.txt'

pdData = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])

positive = pdData[pdData['Admitted'] == 1]

negative = pdData[pdData['Admitted'] == 0]

# 画图观察样本情况

fig, ax = plt.subplots(figsize=(10, 5))

ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o', label='Admitted')

ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x', label='Not Admitted')

ax.legend()

ax.set_xlabel('Exam 1 Score')

ax.set_ylabel('Exam 2 Score')

pdData.insert(0, 'Ones', 1)

plt.show()

# 划分训练数据与标签

orig_data = pdData.values

cols = orig_data.shape[1]

X = orig_data[:, 0:cols - 1]

y = orig_data[:, cols - 1:cols]

# 设置初始参数0

theta = np.zeros([1, 3])

# 选择的梯度下降方法是基于所有样本的

n = 100

runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001)

runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001)

runExpe(orig_data, theta, n, STOP_GRAD, thresh=0.05, alpha=0.001)

runExpe(orig_data, theta, 1, STOP_ITER, thresh=5000, alpha=0.001)

runExpe(orig_data, theta, 1, STOP_ITER, thresh=15000, alpha=0.000002)

runExpe(orig_data, theta, 16, STOP_ITER, thresh=15000, alpha=0.001)

from sklearn import preprocessing as pp

# 数据预处理

scaled_data = orig_data.copy()

scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3])

runExpe(scaled_data, theta, n, STOP_ITER, thresh=5000, alpha=0.001)

runExpe(scaled_data, theta, n, STOP_GRAD, thresh=0.02, alpha=0.001)

theta = runExpe(scaled_data, theta, 1, STOP_GRAD, thresh=0.002 / 5, alpha=0.001)

runExpe(scaled_data, theta, 16, STOP_GRAD, thresh=0.002 * 2, alpha=0.001)

# 设定阈值

def predict(X, theta):

    return [1 if x >= 0.5 else 0 for x in model(X, theta)]

# 计算精度

scaled_X = scaled_data[:, :3]

y = scaled_data[:, 3]

predictions = predict(scaled_X, theta)

correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]

accuracy = (sum(map(int, correct)) % len(correct))

print('accuracy = {0}%'.format(accuracy))

2.3 牛顿法求解高维非线性问题原理简介

 

2.4 牛顿法实现细节

解非线性方程组的牛顿迭代法主程序代码，即newton_iteration.py如下：

import math

import numpy as np

import matplotlib.pyplot as plt

from Dynamic_drawing import image2gif

def newton_iteration(x_k):

    """

    :param x_k: 第k次迭代得到的近似根

    :return x:第k+1次迭代得到的近似根x_{k+1}

    """

    x = [0, 0]

    x[0] = ((x_k[0] - (-x_k[0] ** 3 + x_k[1] ** 2 - 1 + 2 * x_k[0] ** 2 * x_k[1] - 2 * x_k[1] ** 2 - 2 * x_k[1]))

            / (4 * x_k[0] * x_k[1] - 3 * x_k[0] ** 2))

    x[1] = ((x_k[1] - (

            -2 * x_k[0] ** 4 + 2 * x_k[0] * x_k[1] ** 2 - 2 * x_k[0] + 3 * x_k[0] ** 4 - 3 * x_k[0] ** 2 * x_k[

        1] - 3 * x_k[0] ** 2)) / (4 * x_k[0] * x_k[1] - 3 * x_k[0] ** 2))

    return x

# 最大模范数

def norm(ture_u, uh):

    ture_u = np.array(ture_u)

    uh = np.array(uh)

    e = max(abs(ture_u - uh))

    return e

if __name__ == '__main__':

    N = 100

    accurate = 1e-3

    item = 0

    x = [-1.5, 0.5]

    s = [x]

    Loss_list = []

    print("迭代次数：%d" % item, end="\n")

    print("近似根:", x)

    x = newton_iteration(x)

    s.append(x)

    plt.scatter(s[item][0], s[item][1], s=20, c='b', marker='x', label='Initial value')

    plt.legend()

    plt.title("iteration times:" + str(item))

    plt.savefig('./iteration_process/iteration_' + str(item) + '.png')

    item += 1

    print("迭代次数：%d" % item, end="\n")

    print("近似根:", x)

    # print("s:", s)

    print("max|x_%d - x_%d| =" % (item, item - 1), norm(s[item], s[item - 1]))

    loss = norm(s[item], s[item - 1])

    Loss_list.append(loss)

    plt.scatter(s[item][0], s[item][1], s=20, c='k', marker='o')

    plt.title("iteration times:" + str(item))

    plt.savefig('./iteration_process/iteration_' + str(item) + '.png')

    while norm(s[item], s[item - 1]) >= accurate and item < N:

        x = newton_iteration(x)

        s.append(x)

        item += 1

        print("迭代次数：%d" % item, end="\n")

        print("近似根:", x)

        # print("s:", s)

        print("max|x_%d - x_%d| =" % (item, item - 1), norm(s[item], s[item - 1]))

        loss = norm(s[item], s[item - 1])

        Loss_list.append(loss)

        plt.scatter(s[item][0], s[item][1], s=20, c='k', marker='o')

        plt.title("iteration times:" + str(item))

        plt.savefig('./iteration_process/iteration_' + str(item) + '.png')

    # 绘图

    print('=' * 55)

    print('迭代结束'.center(55))

    print('-' * 55)

    plt.close('all')

    plt.title('Error curve')

    plt.xlabel('loss vs. epoches')

    plt.ylabel('loss')

    plt.plot(range(0, item), Loss_list, label='Loss')

    plt.savefig('Error_curve.png')

    # plt.show()

    print('已生成"误差曲线图"，请打开文件"Error_curve.png"查看')

    print('-' * 55)

    print('准备绘迭代过程动态图')

    image2gif.image2gif('iteration')

    print('=' * 55)

绘制迭代过程gif图像模块image2gif.py如下：

注:为使得程序正常运行,需要在当前目录新建文件夹Dynamic_drawing,并将image2gif.py放入其中。

import glob

import imageio

import os

def image2gif(project_name):

    """

将多张图片生成gif动图

    Args:

        project_name:图片名称

    """

    outfilename = str(project_name) + ".gif"  # 转化的GIF图片名称

    filenames = glob.glob('./iteration_process/'+str(project_name)+'*.png')

    filenames = sorted(filenames, key=lambda x: int((os.path.basename(x).split('.')[0]).split('_')[-1]))

    frames = []

    num = 0

    for image_name in filenames:

        im = imageio.imread(image_name)

        frames.append(im)

        print("\r正在读取第%d张图片！" % num, end=" ")

        num += 1

    print('读取完成！')

    print('正在绘制训练过程动态图···')

    imageio.mimsave(outfilename, frames, 'GIF', duration=0.1)  # 生成方式也差不多

    print('绘制完成，请打开文件"'+str(project_name)+'.gif"查看')

3. 实验具体步骤及结果

3.1 梯度下降法求解录取问题结果

为了使得结果更好，测试了几个不同步长，不同梯度下降方式（迭代停止次数：STOP_ITER设定迭代次数，STOP_COST根据损失值停止，以及STOP_GRAD根据梯度值停止）的结果，分析比较得出了较好情况。

结果如下：

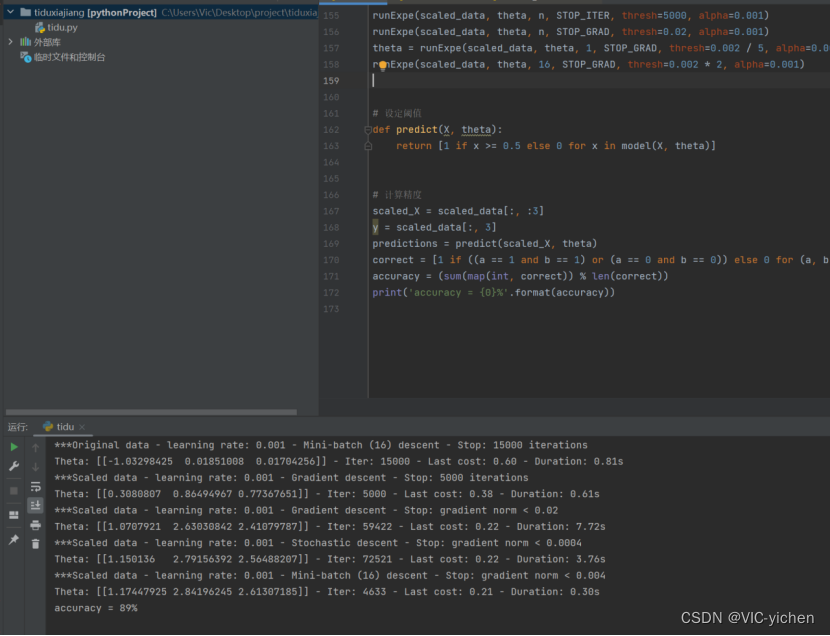
3.2 牛顿法求解给出问题结果

在这里我可视化出了每次迭代后得到的点图，存在newton文件夹下的iteration_process文件夹中。并且将其利用image2gif.py合成为一个gif动图，是newton文件夹中的iteration.gif。且生成误差曲线图，为newton文件夹中的Error_curve.png。

运行结果如下：

  

 

动图无法附在这里，我就共放5张在这里了。

  

 

 

 

 

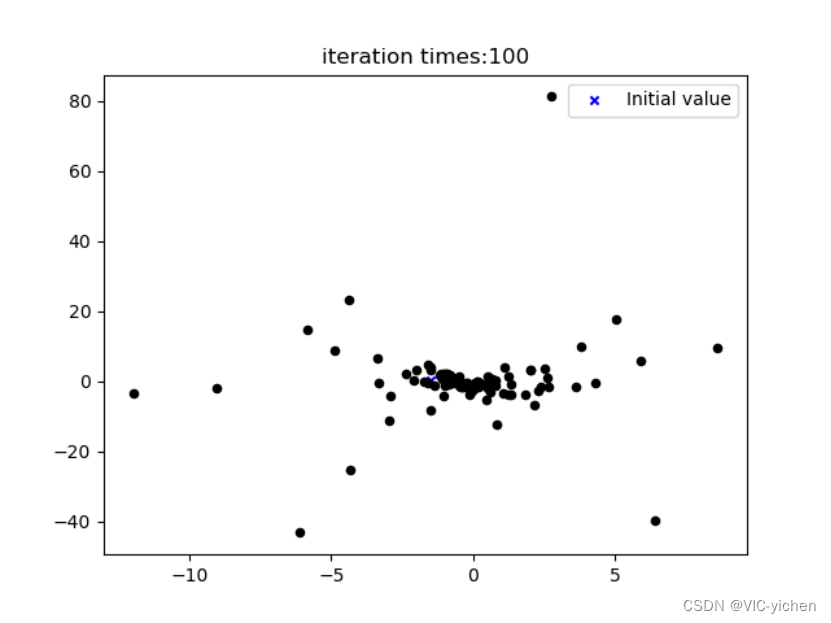
结论

首先是逻辑回归问题，其形式简单，模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响，某个特征的权重值比较高，那么这个特征最后对结果的影响会比较大。

模型效果不错，训练速度较快，资源占用小，方便输出结果调整，但准确率并不是很高，很难处理数据不平衡的问题，处理非线性数据较麻烦。

用梯度下降求解逻辑回归模型需要通过经验或尝试选定步长和方法，这样才能拟合得到最佳效果。

牛顿法求解高维问题具有优势，因为其为二阶泰勒展开，更加精确。

参考文献

1. 卢豆子. 机器学习算法整理（二）梯度下降求解逻辑回归 python实现. 2018-01-28. [DB/OL].  https://www.cnblogs.com/douzujun/p/8370993.html
2. Flechazo_z. 机器学习——逻辑回归（梯度下降法、牛顿法）. 2023-02-26. [DB/OL]. https://blog.youkuaiyun.com/weixin_43973089/article/details/124508746
3. 小松qxs.梯度下降法与牛顿法. 2019-01-28. [DB/OL]. https://www.jianshu.com/p/d892d0d13b6d
4. 图灵的猫. 解非线性方程组的牛顿迭代法(附Python代码). 2021-10-12. [DB/OL]. https://www.jianshu.com/p/406c36d6f593
5. CHERISHGF. 【案例】梯度下降求解逻辑回归. 2021-12-08.  [DB/OL]. https://blog.youkuaiyun.com/CHERISHGF/article/details/121775129