史上最简：深度学习通俗入门教程(1)——了解神经网络

1. 神经网络

神经网络，是代数式的图形表示。例如，下面这个代数式：
$$y=3cos(2x_1+4x_2)+7sin(8x_1+3x_2)\text{\hspace{1em}(1)}$$
可以用图形表示成下面神经网络形式：

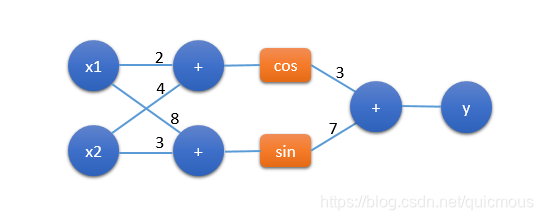
神经网络包括节点和连线，节点 $x_1,x_2$ 是输入， 节点 $y$ 是输出，中间的节点 $+,cos,sin$ 代表运算，连线上的数字代表连线的权重，要与输入数据相乘。例如，下面的图形表示 $2x_1+4x_2$ :

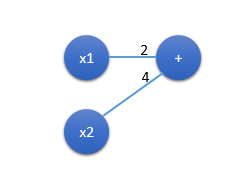
神经网络模型把复杂计算公式的计算过程直观展示出来，更容易理解。

2. 连接、激活函数

一般代数式内部存在线性组合和非线性计算两种运算形式。上面(1)中，存在3个线性组合运算和2个非线性运算。下图展示了3个线性组合运算。两个非线性计算分别是 $cos,sin$ 函数。

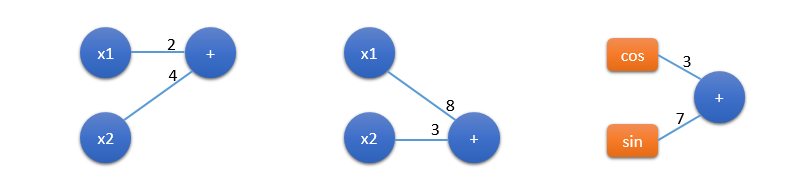
线性组合运算通常用上面这种节点+连接的形式表示， 非线性运算节点通常称为激活函数。

关于激活函数：如果神经网络没有非线性函数，神经网络模型只能实现线性变换运算，无法表达复杂的非线性运算。因此，非线性函数的引入，激活了神经网络模型在非线性问题方面的处理能力。我觉得，这可能就是激活函数名称的来历吧。

3. 二分类问题

我记得小时候读过一本天气预报方面的科普读物，介绍了一种简易的天气预报方法。说是每天记录一下当天的气温 x1 和气压 z2，然后，如果第二天天气晴，就在平面坐标系的 (x1, x2) 位置画一个红圈，如果第二天阴雨，就在 (x1, x2) 位置画一个篮圈。数据积累多了，我们会发现，红圈和篮圈之间实际上可以用一条线分开。

利用这条分界线，就可以预报天气。如果今天的(x1, x2) 落在红圈一侧，就预报明日晴天，否则就预报阴雨。具体参加下面的图形。

其实这就是机器学习的一个雏形——利用已知的观测数据，总结出数据的分布规律，然后用来预测未来的结果。已知的观测数据我们称为“训练样本”，总结规律的过程称之为“学习”，最后得到的预测公式称之为“算法模型”。

3.1 线性可分问题

假设下图平面坐标系内两组点，可以用直线 $w_1{x}_1+w_2{x}_2+w_0=0$ 分开，也就是说这两组点是线性可分的。

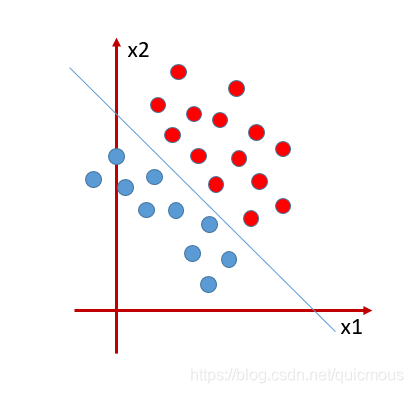
可以用代数式$w_1{x}_1+w_2{x}_2+w_0$ 的符号判断给定的坐标属于哪一组。

借助于符号函数 $sign$ ， 可以把计算结果变换成 $0$ 和 $1$， 以便借助逻辑运算实现更复杂的功能。
$$y=sign(w_1{x}_1+w_2{x}_2+w_0)$$
其中，
$$sign(x)=\{\begin{array}{llc}1& & (x>0)\\ 0& & (x\le 0)\end{array}$$

对应的网络模型如下：

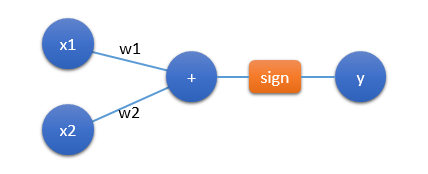
3.2 实现逻辑运算

把输出结果限在 $0,1$ 两种结果上，令 true = 1， false = 0，可以实现逻辑运算。那么逻辑运算是否能用神经网络描述呢？参见下表：

逻辑表达式	代数式
p and q	sign(p+q-1.5)
p or q	sign(p+q-0.5)
p = not(q)	p = 1-q
p = not(sign(x))	p = sign(-x)

3.3 凸集分类问题

下图所示的正样本集合，

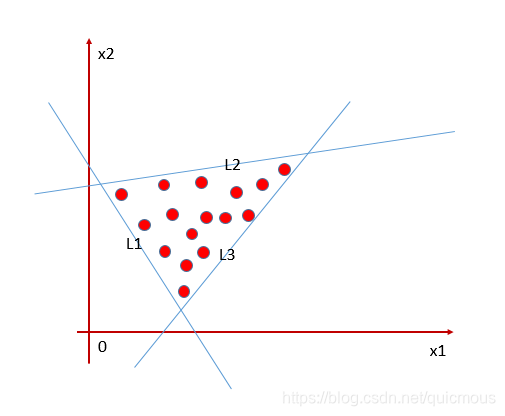
可以用下面约束条件来表示：

$$\begin{gathered} w_{11}{x}_1+w_{12}{x}_2+w_1>0 \\ {w}_{21}{x}_1+w_{22}{x}_2+w_2>0 \\ {w}_{31}{x}_1+w_{32}{x}_2+w_3>0 \\ \text{\hspace{1em}(2)} \end{gathered}$$
令
$$\begin{gathered} y_1=sign(w_{11}{x}_1+w_{12}{x}_2+w_1) \\ {y}_2=sign(w_{21}{x}_1+w_{22}{x}_2+w_2) \\ {y}_3=sign(w_{31}{x}_1+w_{32}{x}_2+w_3) \\ z=sign(y_1+y_2+y_3-2.5)\text{\hspace{1em}(3)} \end{gathered}$$
于是，$z=1$ 时，样本 $(x_1,x_2)$ 是正样本。(3)式对应的神经网络模型图如下：

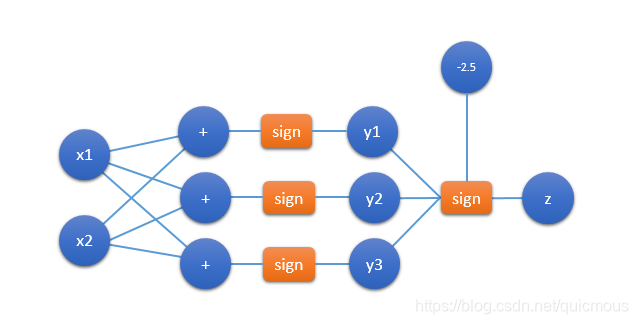
图中，$y_1,y_2,y_3$ 后面的加法节点省略了。一般情况下，模型图会省略掉加法节点，以便简化图形。

3.4 更复杂的分类问题

复杂区域总可以表示成若干凸集的并集。有了前面的基础，我们可以解决更一般的分类问题。下图的正样本区域由两个凸集（三角形区域）的并集构成。

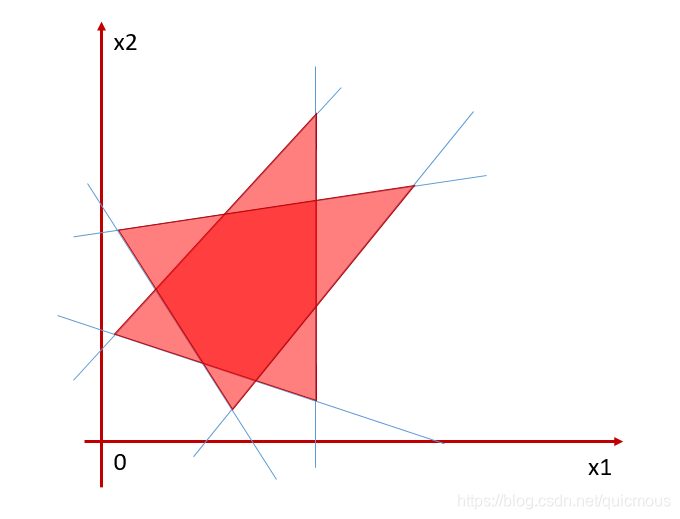
分类计算模型如下：
$$\begin{gathered} --area1-- \\ {y}_1=sign(w_{11}{x}_1+w_{12}{x}_2+w_1) \\ {y}_2=sign(w_{21}{x}_1+w_{22}{x}_2+w_2) \\ {y}_3=sign(w_{31}{x}_1+w_{32}{x}_2+w_3) \\ {z}_1=sign(y_1+y_2+y_3-2.5) \\ --area2-- \\ {y}_4=sign(w_{411}{x}_1+w_{412}{x}_2+w_4) \\ {y}_5=sign(w_{521}{x}_1+w_{522}{x}_2+w_5) \\ {y}_6=sign(w_{631}{x}_1+w_{632}{x}_2+w_6) \\ {z}_2=sign(y_4+y_5+y_6-2.5) \\ --result-- \\ z=sign(z_1+z_2-0.5) \end{gathered}$$

网络模型图如下：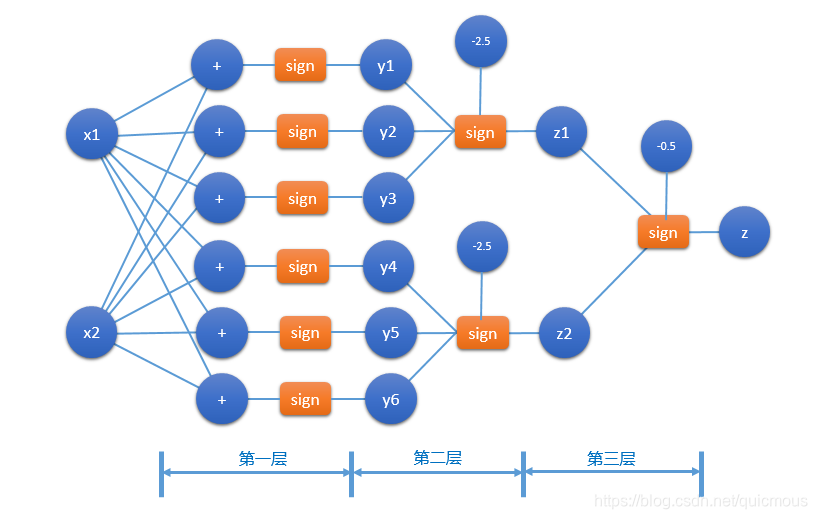
通常我们把激活函数和它前面的线性组合运算组成的单元称为“神经元”。不考虑输入层和输出层，上面的网络模型中存在三个计算网络层：第一层构造了 6 条直线，第二层构造了 2 个三角形， 第三层利用 z = z1 or z2 的关系，给出最终判定结论。

小结

到目前为止，神经网络的结构和原理的核心内容就基本到位了。我们已经能够根据自己对问题的分析，手工构建出网络模型，实现分类算法。

我们的例子中，数据 $(x_1,x_2)$ 是二维的。对于高维度数据分类问题，人工很难确定网络中间层的结构，因此，寻找自动生成网络中间层的方法，是神经网络必须解决的问题。后续课程讲介绍如何利用样本数据，训练生成神经网络模型。