所有可达路径

卡码网题 C#版本

98. 所有可达路径

题目描述

给定一个有 n 个节点的有向无环图，节点编号从 1 到 n。请编写一个函数，找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。

输入描述

第一行包含两个整数 N，M，表示图中拥有 N 个节点，M 条边

后续 M 行，每行包含两个整数 s 和 t，表示图中的 s 节点与 t 节点中有一条路径

输出描述

输出所有的可达路径，路径中所有节点之间空格隔开，每条路径独占一行，存在多条路径，路径输出的顺序可任意。如果不存在任何一条路径，则输出 -1。

注意输出的序列中，最后一个节点后面没有空格！ 例如正确的答案是 `1 3 5`,而不是 `1 3 5 `， 5后面没有空格！

输入示例

5 5
1 3
3 5
1 2
2 4
4 5

输出示例

1 3 5
1 2 4 5

提示信息

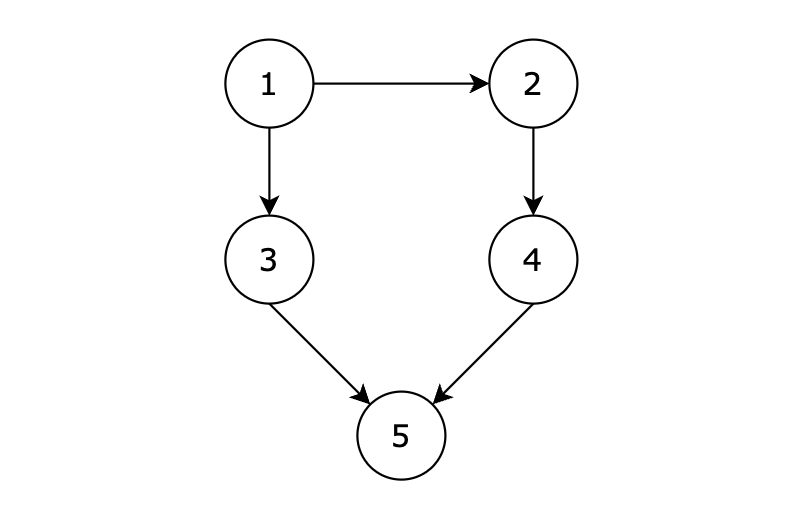
用例解释：

有五个节点，其中的从 1 到达 5 的路径有两个，分别是 1 -> 3 -> 5 和 1 -> 2 -> 4 -> 5。

因为拥有多条路径，所以输出结果为：

1 3 5
1 2 4 5

或

1 2 4 5
1 3 5
都算正确。

数据范围：

• 图中不存在自环
• 图中不存在平行边
• 1 <= N <= 100
• 1 <= M <= 500

 

第一段代码

for (int i = 0; i < graph[x].Length; i++)

{ int next = graph[x][i];

path.Add(next);

Dfs(graph, next);

path.RemoveAt(path.Count - 1); }

这里使用的是 graph[x].Length，因为 graph 是一个邻接表，每个 graph[x] 是一个列表，表示节点 x 的所有邻居节点。因此，您需要遍历该列表的所有元素。

第二段代码

for (int i = 1; i <= n; i++)

{ if (graph[x, i] == 1)

{ path.Add(i);

Dfs(graph, i, n);

path.RemoveAt(path.Count - 1); }

}

在这里，使用的是一个邻接矩阵（假设 graph 是一个二维数组），n 是节点的总数。这段代码循环到 n 是因为需要检查节点 x 是否与每个可能的节点相连。具体来说，循环条件是 i <= n，在每次迭代中检查 graph[x, i] 是否为 1，以确定节点 x 是否与节点 i 直接相连。

总结

• 邻接表：使用 graph[x].Length 是因为每个 graph[x] 是一个列表，直接表示节点 x 的所有邻居。
• 邻接矩阵：使用 i <= n 是因为需要检查所有可能的节点（1 到 n），并通过 graph[x, i] 来判断它们之间的连接关系。

string.Join 是 C# 中一个非常有用的方法，用于将字符串数组或集合中的元素连接成一个单一的字符串。它允许您指定一个分隔符，作为连接各个元素的中间字符。

语法

string.Join(string separator, IEnumerable<string> values);

参数

• separator：一个字符串，用作连接元素之间的分隔符。
• values：要连接的字符串集合或数组。

示例

假设您有一个字符串数组：

string[] words = { "Hello", "World", "!" };

使用 string.Join 可以将这些单词连接成一个完整的句子：

string result = string.Join(" ", words); // 结果是 "Hello World !"

//声明邻接矩阵的方法
using System;
using System.Collections.Generic;
public class MainClass {
    List<IList<int>> result=new List<List<int>>(); //存放结果
    List<int> path=new  List<int>(); //收集的路径
    
    
    public void DFs(int[,] grahp ,int x,int n) //x是当前节点 n是最终节点 
    {
        if(x==n)
        {
            result.Add(new List<int>(path));
            return  ;
        }
        
        for(int i=0;i<=n;i++) //遍历节点 x 链接的所有节点
        {
            if(grahp[x,i]==1)//横向遍历 
            {
                path.Add(i);//将遍历到的节点加进路径中
                DFs(grahp,i,n);//进入下一层递归
                path.RemoveAt(path.Count-1);// 回溯，撤销本节点
            }
        }
        
        
    }
    
    public static void Main(string[] zifu )
    {
        //先处理第一行的MN 
        string[] inputs=Console.ReadLine().Split();
        int n=int.Parse(inputs[0]);
        int m=int.Parse(inputs[1]);
        //编号从1 到n所以申请n+1这么大的二维数组
        int[,] grahp=new int[n+1,n+1];
        
        for(int i=0;i<m;i++)//循环输入节点 存入邻接矩阵
        {
            inputs=Console.ReadLine().Split();
            int s=int.Parse(inputs[0]);
            int t=int.Parse(inputs[1]);
            //使用邻接矩阵标识无向图 1标识s与t相连
            grahp[s,t]=1;
        }
        //无论是怎么走都是从1节点出发
        path.Add(1);
        DFs(grahp,1,n);//开始遍历
        //输出结果
        if(result==0)
        {
            Console.WriteLine(-1);
        }
        else
        {
                for (int i = 0; i < result.Count; i++) {
                    Console.WriteLine(string.Join(" ", result[i]));
                }
        }
    }

}