bellman_ford之判断负权回路

一、题目描述 

二、解题思路-bellman_ford算法

三、完整代码

  四、总结

---

上期文章：

Bellman_ford 算法--带负权值的单源最短路问题，边列表存储-优快云博客

一、题目描述 

比上期文章多了 有回路的条件 ，需要本题我们判断 负权回路，也就是图中出现环且环上的边总权值为负数。

二、解题思路-bellman_ford算法

不熟悉这个算法的可以先看看上期文章 

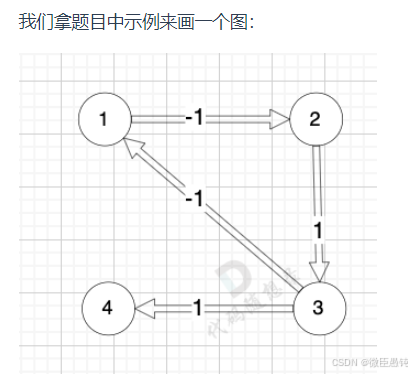
图中 节点1 到 节点4 的最短路径是：节点1 -> 节点2 -> 节点3 -> 节点4，这样的路径总成本为 -1 + 1 + 1 = 1

而图中有负权回路：

        那么我们在负权回路中多绕一圈，我们的最短路径 是不是就更小了 （也就是更低的运输成本）

        节点1 -> 节点2 -> 节点3 -> 节点1 -> 节点2 -> 节点3 -> 节点4，这样的路径总成本 (-1) + 1 + (-1) + (-1) + 1 + (-1) + 1 = -1

        如果在负权回路多绕两圈，三圈，无穷圈，那么我们的总成本就会无限小， 如果要求最小成本的话，你会发现本题就无解了。

···········在 bellman_ford 算法中，松弛 n-1 次所有的边 就可以求得 起点到任何节点的最短路径，松弛 n 次以上，minDist数组（记录起到到其他节点的最短距离）中的结果也不会有改变，而本题有负权回路的情况下，一直都会有更短的最短路，所以 松弛 第n次，minDist数组 也会发生改变。那么解决本题的 核心思路，就是在 kama94.城市间货物运输I 的基础上，再多松弛一次，看minDist数组 是否发生变化。 ※

三、完整代码

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,m;
    cin>>n>>m;
    vector<vector<int>> grid;
    // 初始化图
    for(int i=0;i<m;i++)
    {
        int s,t,v;
        cin>>s>>t>>v;
        grid.push_back({s,t,v});
    }
    int start =1;//起点
    int end=n;//终点
    //初始化最小距离数组
    vector<int> minDist(n+1,INT_MAX);
    minDist[start]=0;
    bool flag=false; //是否有回路
    // 这里我们松弛n次，最后一次判断负权回路
    for(int i=1;i<=n;i++)//松弛次数
    {
        for(auto &edge:grid)
        {
            //取出结点权值
            int from = edge[0];
            int to = edge[1];
            int cost = edge[2];
            if(i!=n)
            {
                if(minDist[from]!=INT_MAX) minDist[to]=min(minDist[to],minDist[from]+cost);
            }else //多加一次松弛判断是否有回路
            {
                if(minDist[from]!=INT_MAX && minDist[from]+cost<minDist[to]) flag =true; //说明第n次松弛会改变mindist数组，有回路
            }
            
        }

    }

   if (flag) cout << "circle" << endl;
    else if (minDist[end] == INT_MAX) {
        cout << "unconnected" << endl;
    } else {
        cout << minDist[end] << endl;
    }
    return 0;


}

  四、总结

        代码真的和上期的差不多，感觉自己真的好笨，一开始写的死代码真的会再遍历第n次，使用两个for大循环，还又定义了一个mindist数组，看了卡哥的代码 wasai 瞬间把代码行数缩短了十几行哈哈哈