上采样（Upsampling）与下采样（ Downsampling）讲解

注：作者为初学者，有些知识不太熟悉，可能描述有误，望见谅。

上采样

概念

        上采样（Upsampling）是深度学习中用于增加特征图空间分辨率的操作，常用于图像分割、超分辨率、生成对抗网络（GAN）等任务。其核心目的是将低分辨率特征图恢复到高分辨率，同时保留或恢复有效信息。

方法（常用 双线性插值、转置卷积）

最近邻插值（Nearest Neighbor Interpolation）

        最近邻插值通过复制最近的像素值实现上采样，计算简单但可能产生锯齿效应。

        适用场景：计算资源有限或对精度要求不高的实时应用（如简单的图像放大）。

PyTorch实现：

        nn.Upsample(scale_factor=2, mode='nearest')中，scale_factor=2是把输入张量的空间尺寸（高和宽）同时放大 2 倍。若输入是 H×W，输出就是 (2H)×(2W)；mode='nearest'是采用最近邻插值算法，输出特征图上每个像素直接复制输入图中“离得最近”的那个像素的值。

import torch.nn as nn

# 定义最近邻上采样层
upsample = nn.Upsample(scale_factor=2, mode='nearest')

# 输入（1张1通道的2x2图像）
input_tensor = torch.rand(1, 1, 2, 2)
output = upsample(input_tensor)
print(output.shape)    # 输出形状：[1, 1, 4, 4]

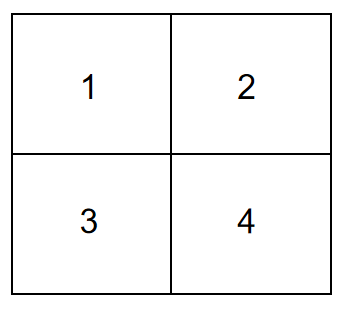
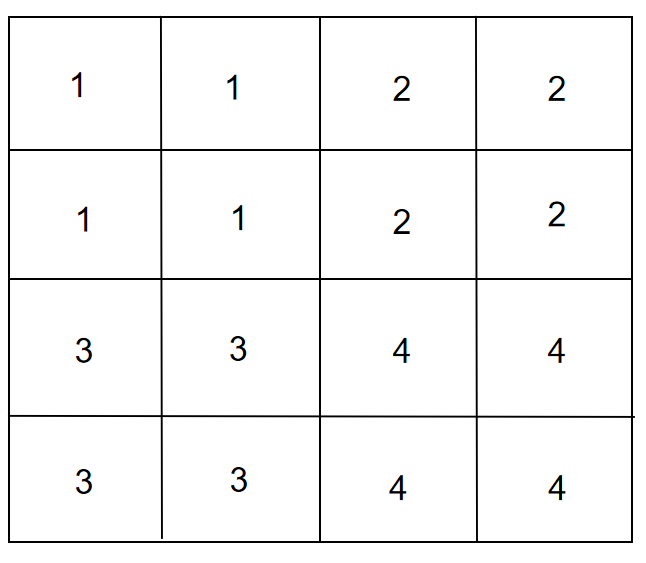
双线性插值（Bilinear Interpolation）

        双线性插值通过对周围4个像素的加权平均计算新像素值，计算简单且无需额外参数，适合对计算资源敏感的场景。但其插值权重固定，无法根据任务需求优化，可能导致细节恢复不足。通常作为轻量级替代方案或与其他方法结合使用。

        语义分割、目标检测、超分辨率等“解码器”部分，80% 以上都会先拿它做“粗放大”，再视情况接别的模块。适用场景为需要平滑过渡的自然图像上采样（如医学影像、普通照片）。

        参数align_corners=True：决定“坐标网格”如何对齐。

True：输入最左上角像素中心与输出最左上角像素中心严格重合，边缘像素也严格对齐。

False：像素被视为“小方块”，网格从 -1+1/W 到 1-1/W，边缘外扩 0.5 像素。

PyTorch实现：

upsample = nn.Upsample(scale_factor=2, mode='bilinear', align_corners=True)

# 示例输入
input_tensor = torch.rand(1, 3, 16, 16)
output = upsample(input_tensor)
print(output.shape)  # 输出形状：[1, 3, 32, 32]

转置卷积（Transposed Convolution） （U-NET使用）

        转置卷积通过可学习的核进行上采样，能适应数据分布但可能引发棋盘效应。

        适用场景：需要端到端学习的任务（如语义分割、图像生成）。

        转置卷积在深度学习中有时也称作反卷积，实现上并不“逆运算”，只是用转置后的卷积核权重做稀疏卷积。

步骤

（1）先把输入每个像素周围补零（stride−1 行/列零）：4×4 变成 7×7（因为 stride=2，相邻像素间插 1 行 1 列零）。如下图：

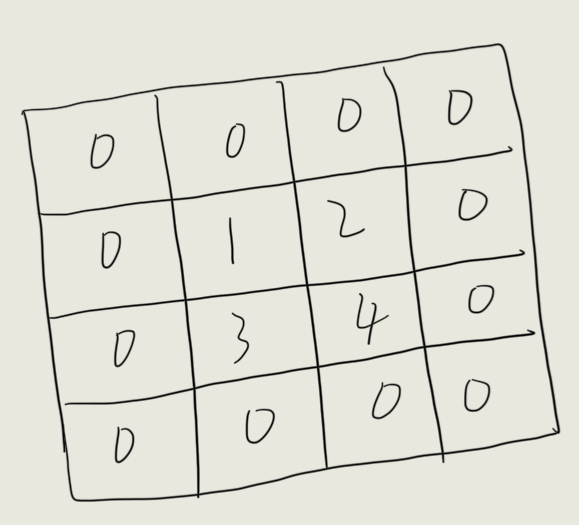
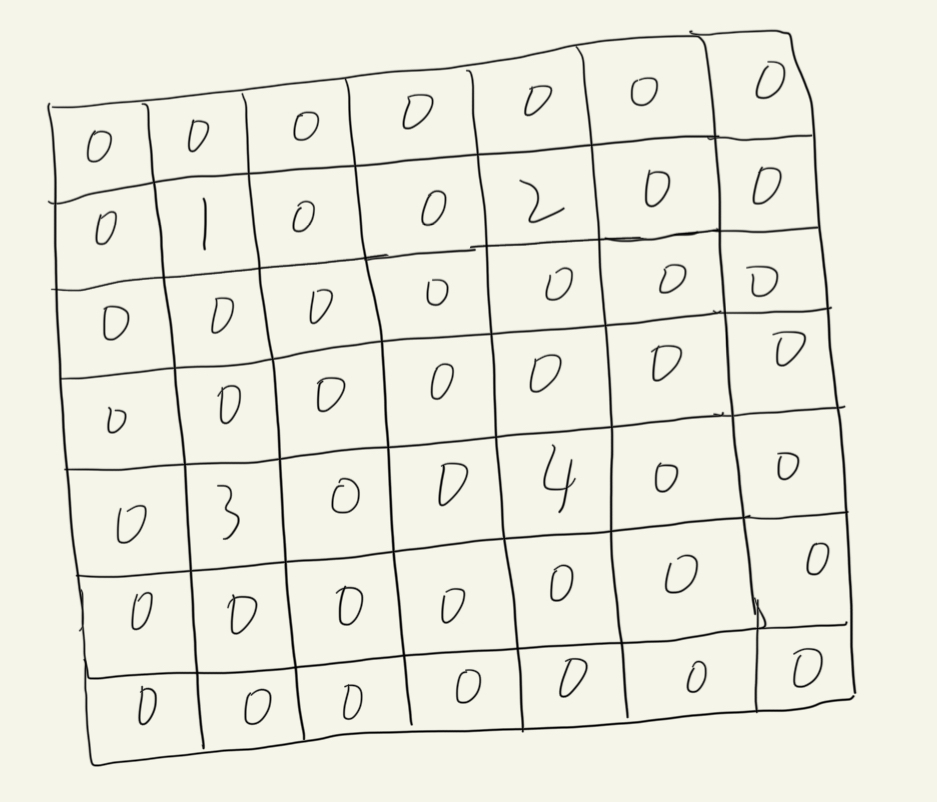
（2）再在四周再补 padding 圈零（这里 padding=1）：7×7 → 9×9。（图略）

（3）用 3×3 核做普通卷积（步长=1）：9×9 经 3×3 卷积 ⇒ 7×7，但 PyTorch 又在最右/最下再补 output_padding=1，最终得到 8×8。

输出尺寸计算方法

公式：out = (in −1)×stride − 2×padding + kernel + output_padding

如：kernel=3，stride=2，padding=1，output_padding=1

输入 4×4 ⇒ (4−1)×2 −2×1 +3 +1 = 6−2+3+1 = 8
所以 4×4 → 8×8（通道数不变，仍为 1）

PyTorch实现：

import torch
import torch.nn as nn

# 定义转置卷积层
trans_conv = nn.ConvTranspose2d(
    in_channels=1, 
    out_channels=1,
    kernel_size=3,
    stride=2,
    padding=1,
    output_padding=1,
    bias=False
)

# 生成4x4的输入张量（模拟单通道图像）
input_tensor = torch.arange(16, dtype=torch.float32).reshape(1, 1, 4, 4)
print("输入尺寸:", input_tensor.shape)

# 执行转置卷积
output = trans_conv(input_tensor)
print("输出尺寸:", output.shape)

# 验证维度计算公式
calculated_size = (input_tensor.shape[2] - 1) * 2 - 2 * 1 + 3 + 1
print("计算尺寸应等于:", calculated_size)
 

像素洗牌（Pixel Shuffle）

        像素洗牌将通道维度信息重组到空间维度，常用于超分辨率任务，效率高于转置卷积。

        适用场景：高质量图像超分辨率（如ESPCN、Real-ESRGAN）。

PyTorch实现：

# 先通过卷积增加通道数，再应用PixelShuffle
conv = nn.Conv2d(64, 256, kernel_size=3, padding=1)
pixel_shuffle = nn.PixelShuffle(upscale_factor=2)

# 示例输入
input_tensor = torch.rand(1, 64, 16, 16)
x = conv(input_tensor)
output = pixel_shuffle(x)
print(output.shape)  # 输出形状：[1, 64, 32, 32]

反池化（Unpooling）

        反池化编码器用 MaxPool 下采样时把“最大值的 spatial index”记下来，解码器把值 原路放回去，其余填零，从而：

• 保持边缘稀疏、定位精确；

• 无参数、无学习；

• 但只恢复“最大值”信息，非最大位置永远为零。

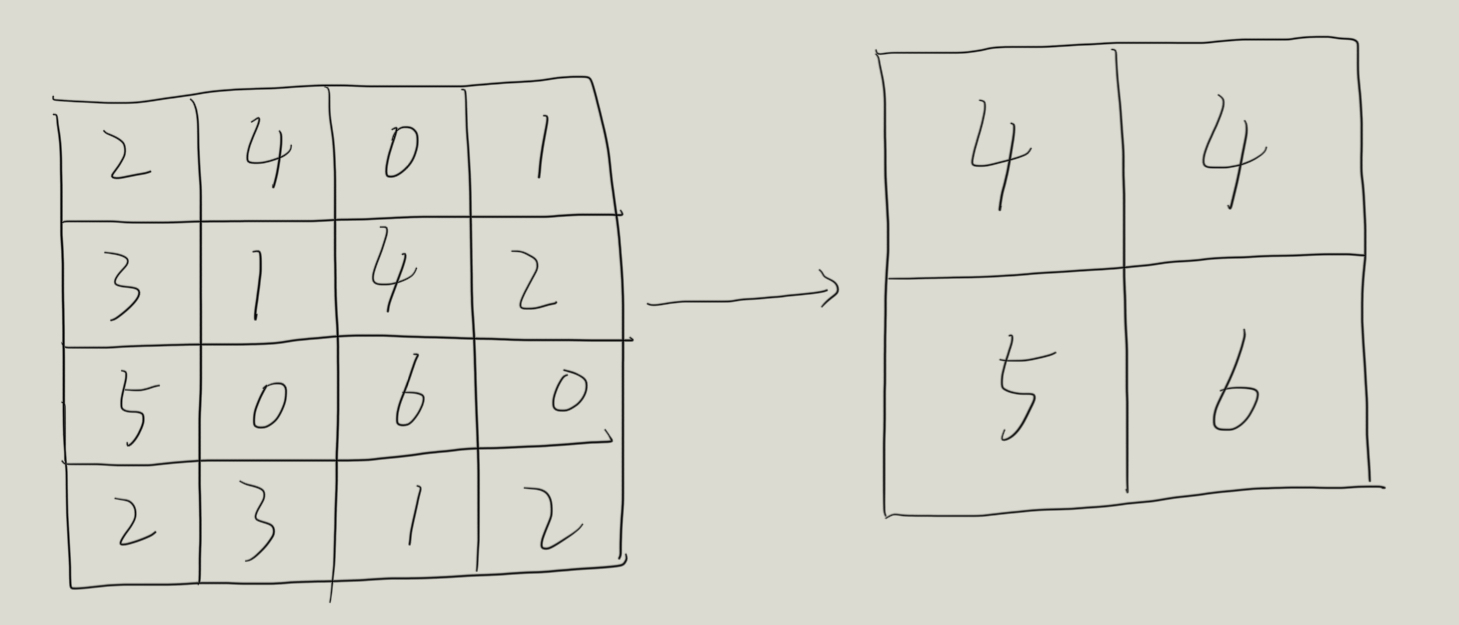
        反池化后：

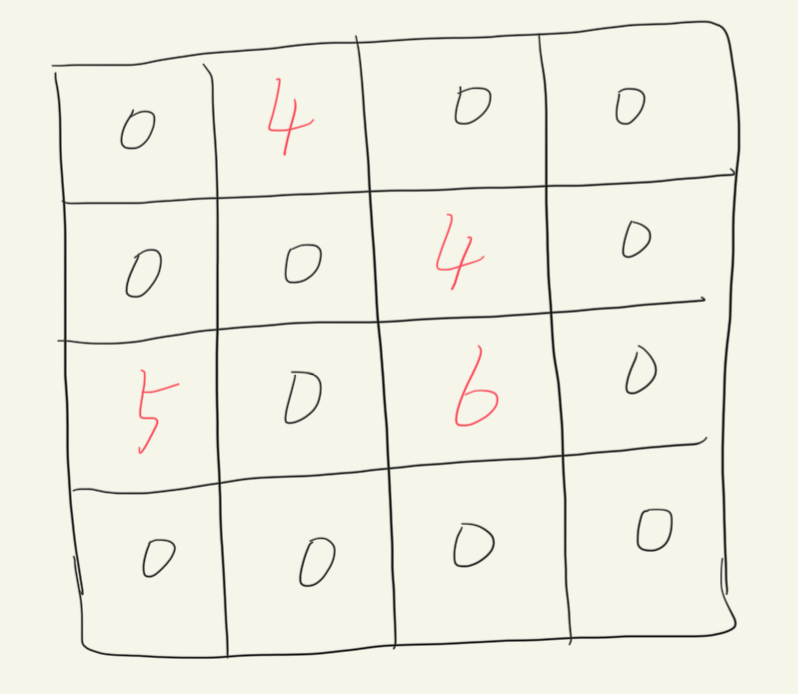
PyTorch实现：

        nn.MaxPool2d(2, return_indices=True)中：

        2等价于 kernel_size=2，表示池化窗口大小 2×2；

        return_indices=True：前向传播时不仅返回池化结果，还会把“每个最大值在滑动窗口里的平面索引”一并返回。这些索引后续要交给 MaxUnpool2d 做反池化，告诉它“原来最大值在哪个位置”。

pool = nn.MaxPool2d(2, return_indices=True)
unpool = nn.MaxUnpool2d(2)

# 示例输入
input_tensor = torch.rand(1, 1, 4, 4)
x, indices = pool(input_tensor)
output = unpool(x, indices)
print(output.shape)  # 输出形状：[1, 1, 4, 4]

下采样

下采样的概念

        下采样（Downsampling）是减少数据空间分辨率或时间分辨率的过程，通过降低特征图尺寸或减少数据量来压缩信息。在深度学习中，下采样常用于减少计算量、扩大感受野或提取高层特征。

方法

方法选择建议

（1）注重位置信息：优先使用步长卷积或空洞卷积。

（2）需要抗噪声：选择最大池化或平均池化。

（3）多尺度任务：考虑SPP或类似结构。

最大池化（Max Pooling）：

        在局部窗口内取最大值作为输出。
优点：保留显著特征，抑制噪声，计算高效。
缺点：丢失位置细节信息，可能产生过拟合。

PyTorch示例：

import torch.nn as nn

max_pool = nn.MaxPool2d(kernel_size=2, stride=2)
input_tensor = torch.randn(1, 3, 64, 64)  # (batch, channel, height, width)
output = max_pool(input_tensor)
print(output.shape)  # torch.Size([1, 3, 32, 32])

平均池化（Average Pooling）：

        在局部窗口内计算平均值作为输出。
优点：平滑特征，减少噪声影响。
缺点：模糊重要特征，边缘信息可能丢失。

PyTorch示例：

avg_pool = nn.AvgPool2d(kernel_size=2, stride=2)
output = avg_pool(input_tensor)
print(output.shape)  # torch.Size([1, 3, 32, 32])

步长卷积（Strided Convolution）：

        通过设置卷积步长（stride > 1）直接缩小特征图尺寸。
优点：可学习参数保留更多信息，灵活性高。
缺点：可能引入棋盘伪影（checkerboard artifacts）。

PyTorch示例：

conv = nn.Conv2d(3, 64, kernel_size=3, stride=2, padding=1)
output = conv(input_tensor)
print(output.shape)  # torch.Size([1, 64, 32, 32])

空洞卷积（Dilated Convolution）：

        通过增大卷积核间隔（dilation rate）间接扩大感受野。
优点：保持特征图尺寸时扩大感受野。
缺点：小物体信息可能丢失，计算成本较高。

        参数dilation=2： 空洞率=2，把 3×3 核的 9 个采样点间隔拉开，实际覆盖 5×5 的物理区域。

普通卷积：

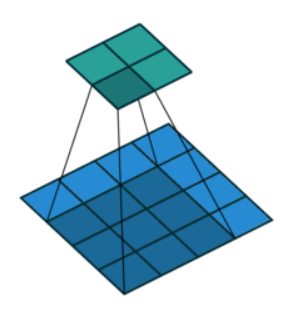
空洞卷积：

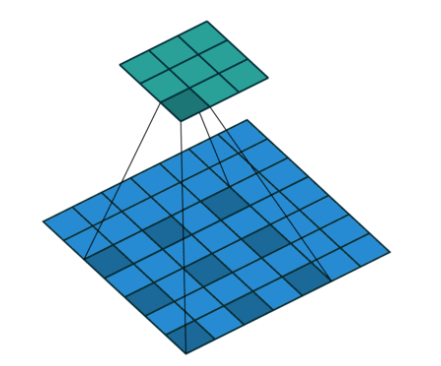
        二者的卷积核大小都是一样的（滑窗的实际大小是一样的），但空洞卷积的滑窗（kernel）元素之间是存在一些间隙的，这些间隙在空洞卷积中成为膨胀因子。

PyTorch示例：

dilated_conv = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=2, dilation=2)
output = dilated_conv(input_tensor)
print(output.shape)  # torch.Size([1, 64, 64, 64])

空间金字塔池化（SPP）：

        多尺度池化后拼接特征，适应不同输入尺寸。
优点：处理可变输入尺寸，增强多尺度特征提取。
缺点：内存占用高，实现复杂。

PyTorch示例：

class SPP(nn.Module):
    def __init__(self):
        super().__init__()
        self.pools = nn.ModuleList([
            nn.MaxPool2d(4, 4),
            nn.MaxPool2d(8, 8),
            nn.MaxPool2d(16, 16)
        ])
    
    def forward(self, x):
        features = [x]
        for pool in self.pools:
            features.append(pool(x))
        return torch.cat(features, dim=1)

spp = SPP()
output = spp(input_tensor)
print(output.shape)  # 依赖输入尺寸