【8】：着色（光照与基本着色模型）

深度

遮挡关系、深度与画家算法

我们已经知道了如何把一个物体画到屏幕上，也就是MVP变换（Model-View-Projection）。现在还遗留一个问题：那就是物体的遮挡关系。

为此，我们可以定义每个物体离着我们摄像机的远近。离得远的就被放在后面，离得近的就被放到前面。

所以前面的东西会遮挡住后面的东西。

我们可以采用所谓的画家算法（painter’s algorithm）：先画最后面的，再画前面的。这样就自然而然满足了遮挡关系。

例如下面这幅画

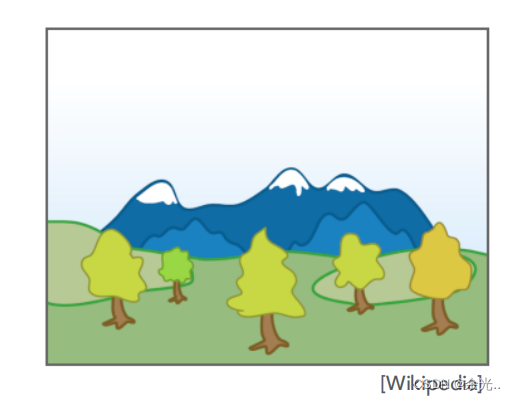
我们先画出远处的山，再画出草地，最后画出树木。这样就满足了遮挡关系。

但是这样的做法有一个缺点：你需要对比每一个物体之间的远近，所以计算量很大。

假如场景中有n个物体。我们需要按照远近距离对n个物体进行排序。排序之后再按照从远到近的顺序依次画出物体。排序算法显然需要O(nlogn)的算法复杂度。

有没有更节约计算量的算法呢？

有的。那就是z-buffer算法。

z-buffer算法（深度缓冲）

说起来，z-buff算法也是很简单。它的中心思想就是：对于像素来说，不需要排序，遮挡了就覆盖上去就好了。

也就是如下算法：

首先初始化所有像素的距离为无穷大。
最外面的两层for循环，一个是对三角形，一个是对像素。
我们对每个像素而言：
假如 当前要画出来的距离更近，那么就覆盖掉原来的像素值，并且把当前的像素值的距离缓存。

这里远近距离是用z值来定义的，所以叫做z-buffer。

这个算法很简单，其实就是寻找最小值的一个算法，相信刷过算法题或者学过算法的人都写过类似的算法。寻找最小值的算法，其算法复杂度是O(n)，显然比画家算法要节约计算量。

下面是个例子。在这里，先画出来红色还是先画出来蓝色都是无所谓的。反正只有最近距离的像素值不会被覆盖掉。 

 目前知识的总结

我们现在已经学会了MVP变换，也学会了光栅化。

我们知道，其实将一个物体渲染的步骤无非以下：

1. 把模型放好（给出模型中各个点的坐标）
2. 把相机放好（把相机摆到标准位置）
3. 对着模型拍一张照片（视图变换，投影变换以及视口变换）
4. 在屏幕上画出这张照片（光栅化）

总而言之，所谓渲染，其实就是照照片。只不过这个照片是电脑画出来的。

着色（shading）

但是，我们还不能表现物体的明暗变化。

也就是说
我们只能画出这样的图形。

但是画不出这样的图形

两者的区别就在于加没加明暗变化。

也就是小孩子涂鸦与素描画的区别。小孩子涂鸦只知道涂抹色块，但是不知道处理明暗。而素描画就是专门处理明暗变化的。有了明暗变化，立体感才会显现出来。

用术语来说，这就是：shading（着色）。

我们接下来就介绍一种着色模型：Blinn-Phong模型。

Blinn-Phong着色模型

在进展之前，我们先讨论下：一张照片的明暗变化是由哪几部分组成的？

我们观察下面这个茶杯。我们发现有：

• 高光
• 漫反射
• 环境光

为此，我们要定义几个参数：

• 视线方向v
• 表面法向n
• 入射光方向I
• 表面的其他参数，例如颜色、光泽…

以上的前三个参数，由于只是表示方向的，所以我们用单位向量表示。

下面我们要分别处理高光、漫反射和环境光。

漫反射（diffuse）

对于漫反射，我们需要考虑两方面的因素：

• 入射角度
• 距离

入射角度对漫反射的影响

先说为什么和入射角度相关。

我们先取一小块单位表面。

• 当光直射表面的时候，接收光照的面积是整个面积，即1。
• 当光与表面有一个夹角的时候（我们用表面法向n与入射光I的夹角theta表示），接收光照的面积只是一部分面积。即小于1。
• 当光与表面完全平行的时候（也就是theta=90°），接收光照的面积为0。

那么具体来说，假如成theta角，接收光照的面积是原来的多少呢？

答案是cos  θ

可以画出如下面第三个图来推导。

显然下面的那块面积正是1⋅cosθ

而由于采用了单位向量，恰好单位向量I与n之间的点积就是cosθ

我们可以认为，只有cosθ的光能量被表面接收了。所以自然亮度要乘以cosθ。

距离对漫反射的影响

另一个影响因素，是距离

对于一个点光源来说，我们想象光向外发射出一个球壳。由于能量守恒的缘故，显然这个球壳越大，能量就约稀薄。也就是单位面积上能够接收到的能量就越小。这和摊煎饼是一个道理，摊的越大，面糊糊越薄。

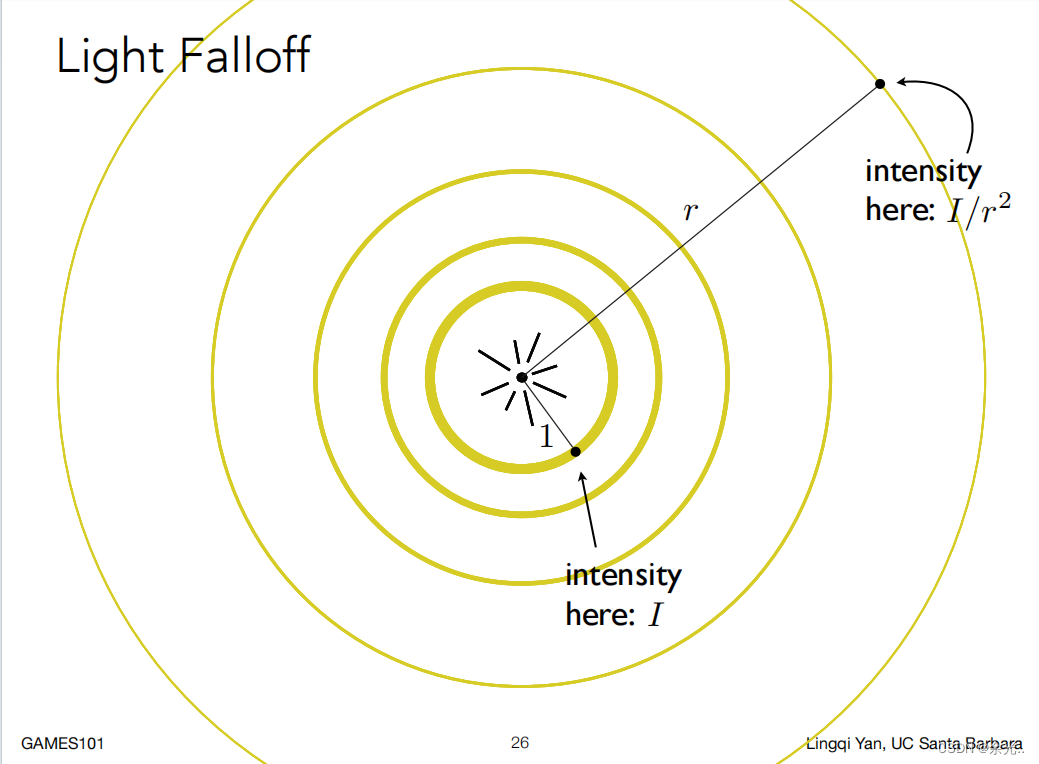
按照什么样的比例衰减呢？

自然是球壳表面积有多大，能量就要均摊多少！

球壳表面积是

所以光的能量自然是按照这个比率来衰减的了！

Lambertian 定律

把上述两点因素结合起来，我们就得到了漫反射的规律，这被称之为Lambertian 定律。

就是下面这个公式

这里要说明：

1. 为什么要用max(0, …)?
   这是为了防止出现负数。而在我们情况里，夹角出现负数是没有意义的。光线不可能从物体的内部照射到物体表面。
2. 为什么要有前面的系数kd?
   首先，我们可以通过这个系数调整漫反射的强度，也就是明暗。其次，假如我们把它设置为向量，还可以表示不同颜色。因为不同颜色的吸收率可能是不同的。我们对每个颜色（RGB）给出一个系数，用来表示这种颜色没有被吸收的占比。这样就可以造成不同颜色的漫反射效果。
3. 为什么没有视线向量v？
   是因为漫反射与视角无关。无论你从哪个方向看过去，漫反射的光都是一样的。

下图展示了左上方光源照射一个球体得到的漫反射图像。可以发现：球体右下部分由于与光线夹角为0，是无法接受光线的，所以是暗的。而随着往左上方，球体表面法向与光源夹角越来越小，所以越来越亮。

不同的图片表示了不同kd的结果。这也可以看出，kd可以调整漫反射的强度。

一句话：漫反射处理的是物体与光源的相对位置（远近和方向）所造成的明暗变化。

高光(Specular Light)

漫反射是与视角无关的，它只和光源与物体的相对位置有关。而高光不仅和光源和物体的相对位置有关，还和观察的角度有关。

具体来说，高光就是镜面反射， 即当观察者的视线与反射光线恰好处在同一角度（或者相距很小角度）的时候，会看到很亮的光点。

如图所示。

那么，做法就很简单了：我们找到反射光线的方向向量（R），再给出一个相机视线的方向向量（v）。我们只要看这两者是不是夹角很小即可。

如何定义夹角呢？显然用cos比较方便。而在第二节课中我们讲过，单位向量的夹角余弦恰好就是单位向量点乘。

所以，我们只要点乘R与v就好了。

这样，就能衡量出两个方向夹角的大小。

1.但是要求出反射光线R向量，虽然不是不可以，但是比较麻烦，计算量大。所以Blinn提出来了一个天才般的想法：
不去计算R与v的夹角余弦，而是去计算v和入射方向I的角平分线 与 表面法线的夹角余弦
于是就定义了这个角平分线为h

这个h被称为：半程向量。

顺带一提，如果不用这个技巧的模型，被称为Phong模型。利用这个技巧的，才叫Blinn-Phong模型。

Blinn-Phong模型大大简化了计算。因为计算反射方向是一件很繁琐的事情（想想看找到某个向量以另一个向量为轴的对称向量，并不是一件很容易的事情）。

2.另外，还需要注意的是。由于我们不允许出现负值（夹角余弦出现负值代表着角度大于90度了，而我们的范围也就是0-90度），所以要加上一个max(0, xxx)。当小于0的时候，取0。

3. 我们观察这个公式，还会发现一点：即max之后还有个alpha次方。这是为什么呢？
这是因为cosin函数太平缓了，不够陡峭，所以高光的范围太大了，为了让高光范围小一点，我们可以取alpha次方。（alpha一般可以取100~200之间）

变动p和ks，我们得到的效果如图所示。

（注：Ls的s代表的是specular）

环境光（ambient）

环境光就用很简单的一个系数代替就好了。这是非常简化的模型。

实际上，若是用更复杂的模型，可以看看全局光照技术。

Blinn-Phong整体效果

将三项加和（漫反射+高光+环境光）
得到效果如下

其中La的a代表ambiant
Ld的d代表diffuse
Ls的s代表specular