Kind of a Blur

 传送门

题意：

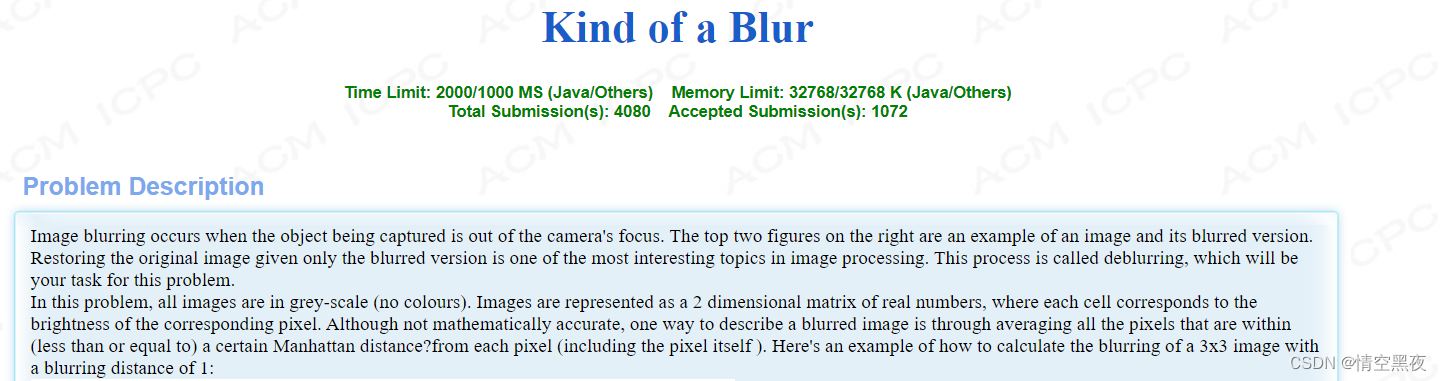
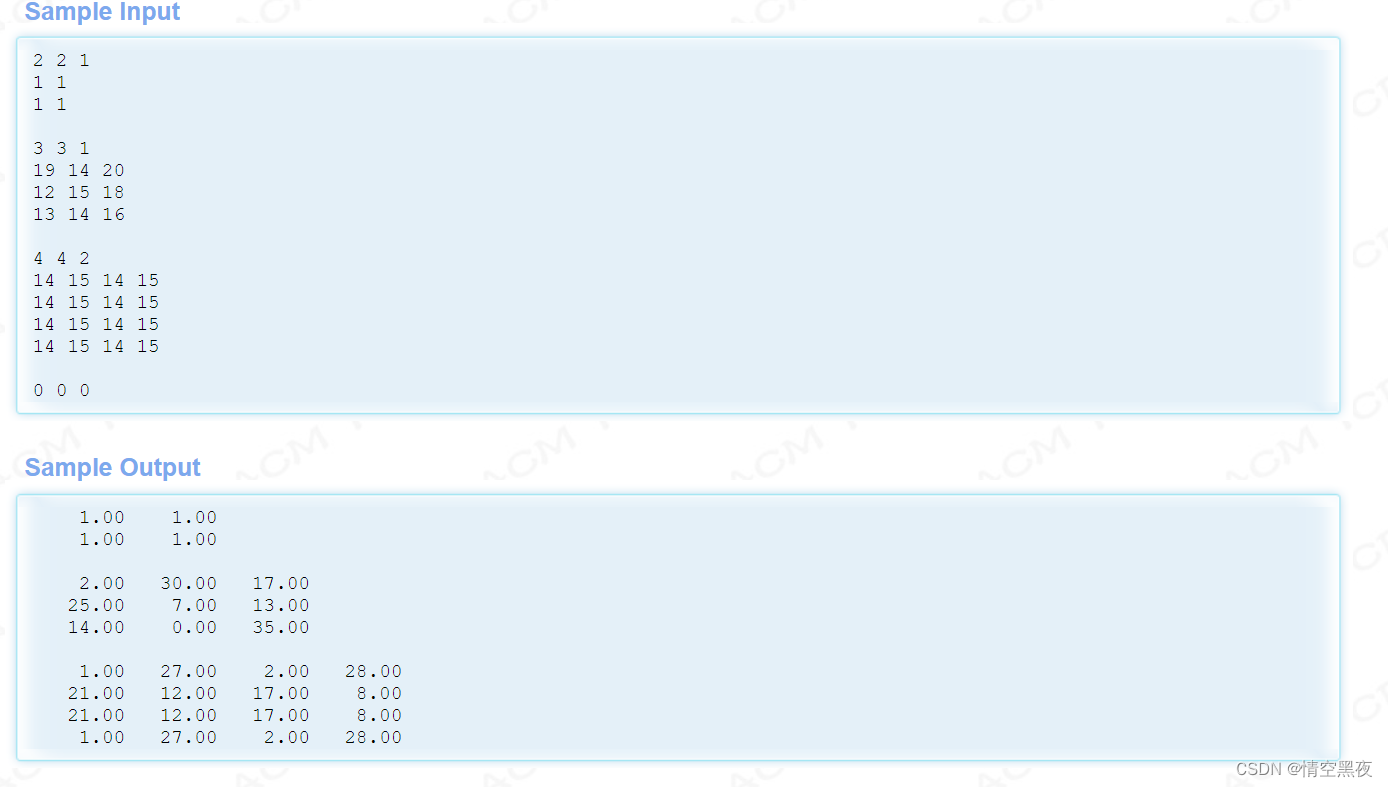
输入w, h, d, 和一个w * h的矩阵，d代表曼哈顿距离，要求构建一个矩阵，是这个矩阵的每个元素的曼哈顿距离之内的元素的平均值，等于题目所给的矩阵。

思路：

要构建的矩阵不知道，那就全部假设是x, 最后只要装换成求解这个方程组即可，数据量只有10，所以很容易想到高斯消元，高斯消元，弄清楚每个方程的值，和这个方程的相关系数，即1，就可以根据这个去列方程。

#include <iostream>
#include <cstring>
#include <cmath>
#include <iomanip>
#define endl '\n'
#define IOS ios::sync_with_stdio(false);
using namespace std;

typedef long long ll;

const double eps = 1e-8;
bool isFirst = true;

struct Matrix
{
	int h, w;
	double m[105][105];
	
	void init(int totalh, int totalw)
	{
		h = totalh;
		w = totalw;
		memset(m, 0, sizeof m);
	}
	
	void Guass()
    {
        for (int i = 0 ; i < h-1 ; i++)
        {
            //交换行（减小误差） 
            int t = i;
            for (int j = i+1 ; j < h ; j++)
            {
                if (fabs(m[j][i]) > fabs(m[t][i]))
                    t = j;
            }
            if (t != i)
            {
                for (int j = 0 ; j < w ; j++)
                    swap(m[t][j],m[i][j]);
            }

            //消元
            for (int j = i+1 ; j < h ; j++)
            {
                if (fabs(m[j][i]) < eps)
                    continue;
                double mul = m[j][i] / m[i][i];
                for (int k = i ; k < w ; k++)
                    m[j][k] -= m[i][k] * mul;
            }
        }

        //反向求解
        for (int i = h-1 ; i >= 0 ; i--)
        {
            if (fabs(m[i][i]) < eps)
                continue;
            for (int j = i+1 ; j < h ; j++)
                m[i][w-1] -= m[i][j]*m[j][w-1];
            m[i][w-1] /= m[i][i];
        }
    }   
};

int main()
{
	//IOS; cin.tie(0), cout.tie(0);
	int w, h, d;
	double a[15][15];
	while (cin >> w >> h >> d)
	{
		if (w == 0 && h == 0 && d == 0)
			break; 
		for (int i = 0; i < h; ++i)
		{
			for (int j = 0; j < w; ++j)
			{
				cin >> a[i][j];
			}
		}
		
		if (isFirst)
		{
			isFirst = false;
		}
		else
		{
			cout << endl;
		}
		
		Matrix ans;
		ans.init(h * w, h * w + 1); 
		
		//高斯消元的不可少的步骤
		for (int i = 0; i < h; ++i)
		{
			for (int j = 0; j < w; ++j)
			{
				int cnt = 0;	//记录一个点的曼哈顿距离能够到达的个数
				for (int k = i - d; k <= i + d; ++k)	//枚举能到达的行 
				{
					if (k < 0 || k >= h)
						continue;
					int left = d - abs(i - k);
					for (int l = j - left; l <= j + left; ++l)
					{
						if (l < 0 || l >= w)
							continue;
						cnt++;
						ans.m[i * w + j][k * w + l] = 1;	//第i * w + j行方程的第k * w + l	
					} 
				} 
				ans.m[i * w + j][h * w] = cnt * a[i][j]; 
			}
		} 
		ans.Guass();
		
		for (int i = 0 ; i < h ; ++i)
        {
            for (int j = 0 ; j < w ; ++j)
                printf ("%8.2lf",ans.m[i * w + j][ans.w - 1]);
            printf ("\n");
        }
	}
	return 0;
}