通过一个实际问题帮助大家熟悉LINGO解决线性规划模型的方式和思路。
【例题】选址问题:
某公司有6个建筑工地,位置坐标为(ai,bi)(公里),水泥日用量为di(吨).
i 1 2 3 4 5 6 a 2 8.75 0.5 5.75 3 7.25 b 3 0.75 4.75 5 6.5 7.75 d 1.25 5 4 7 6 11 假设:料场和工地之间有直线道路.
现有两个料场,位于A(5,1),B(2,7),记(xj,yj),j=1,2,日储量ej各有20吨.
目标:制定每天的供应计划,即从A,B两料场分别向各工地运送多少吨水泥,使总的吨公里数最小。

根据LINGO模型,我们逐个进行建模分析。
根据题目要求,我们可以建立如下的供需模型和相应变量关系。

转换为LINGO语言,定义出集合段:

根据定义好的集,为其赋值,完成数据段:

我们把料场的坐标作为初始段,其实如果这两个位置坐标放在数据段中定义,也无妨

最后是,核心部分,目标与约束段,首当其冲的是,我们要根据题目列出所有的约束条件,这考察的是大家的数学能力,这里就不再详述了。
这是根据题意列出的原始约束条件:

进一步地,我们需要将其简化
便于大家理解,我写出了目标式的简化过程:
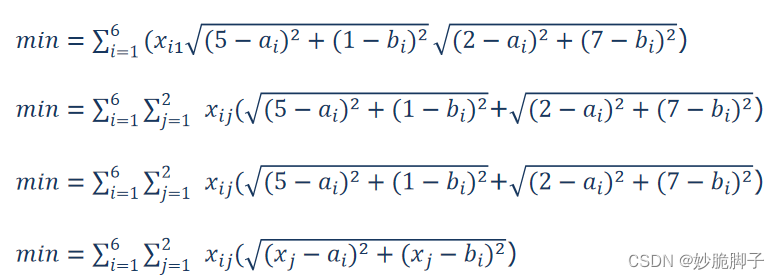
其他简化过程不再详述,最后的简化结果为:
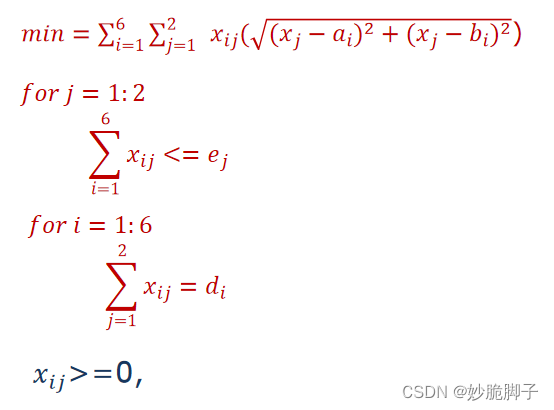
接着,将简化好的式子们转换为LINGO表达式:
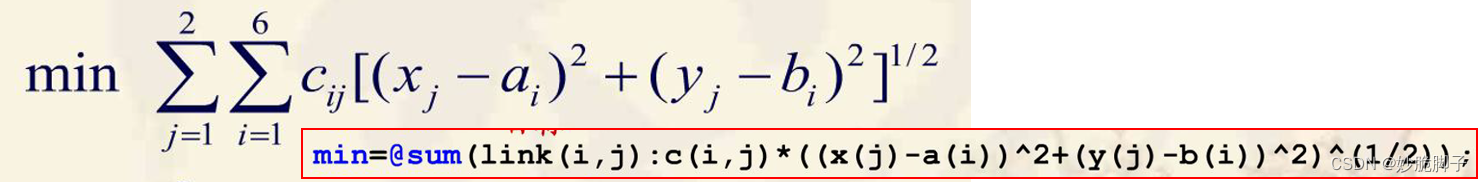


最后,得到完整的LINGO模型
MODEL:
Title Location Problem;
sets:
demand/1..6/:a,b,d;
supply/1..2/:x,y,e;
link(demand,supply):c;
endsets
data:
a=1.25,8.75,0.5,5.75,3,7.25;
b=1.25,0.75,4.75,5,6.5,7.75;
d=3,5,4,7,6,11;
e=20,20;
enddata
init:
x,y=5,1,2,7;
endinit
min=@sum(link(i,j):c(i,j)*((x(j)-a(i))^2+(y(j)-b(i))^2)^(1/2));
@for(demand(i):@sum(supply(j):c(i,j))=d(i););
@for(supply(j):@sum(demand(i):c(i,j))<=e(j););
END
解毕。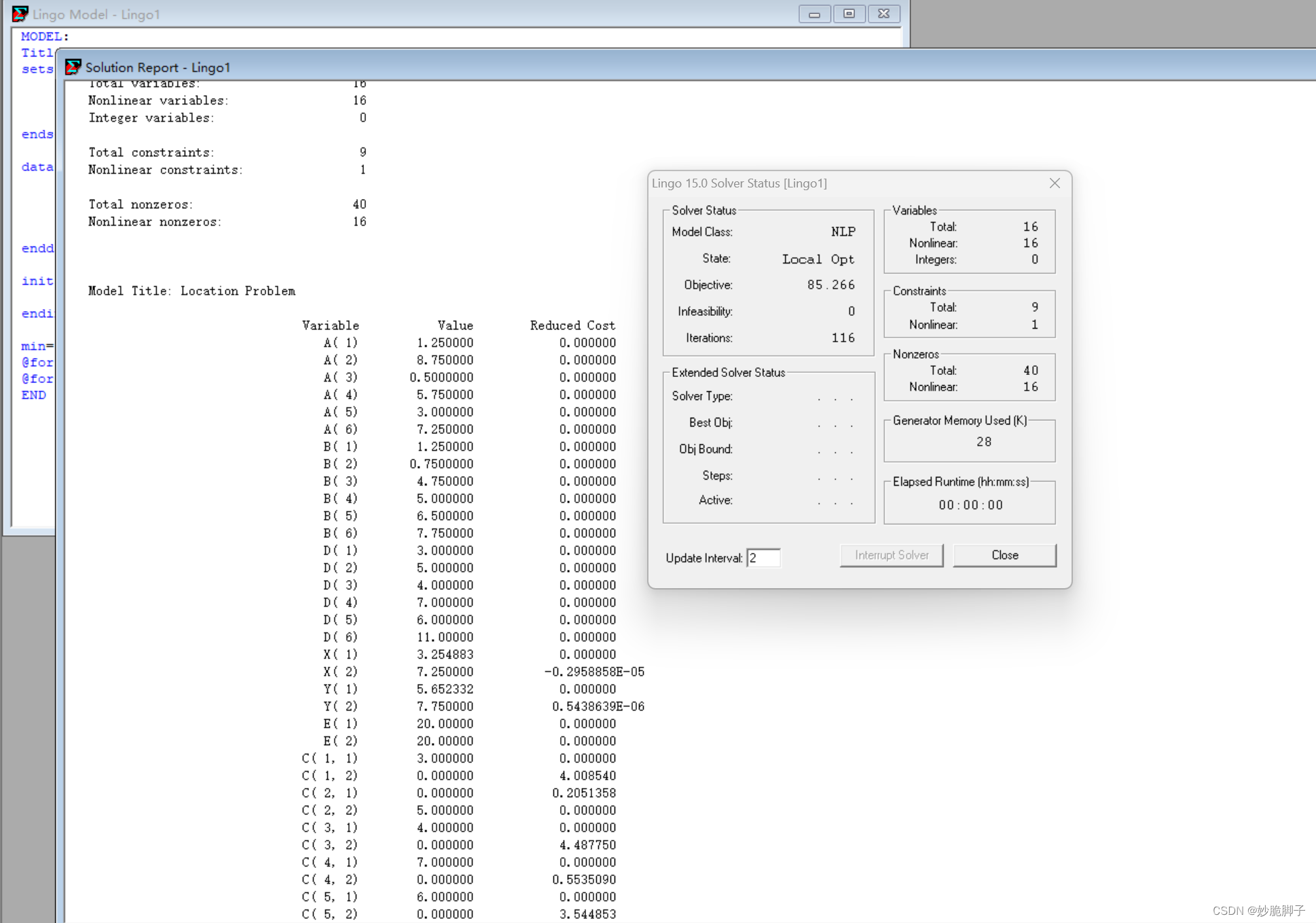























 1806
1806

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








