机器学习分类算法

虾仁不眨眼335

于 2024-09-02 09:32:44 发布

阅读量636

点赞数 21

文章标签：机器学习分类人工智能

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/qq_62085589/article/details/141643940

版权

机器学习常见分类算法

逻辑回归（Logistic Regression）

逻辑回归也称作logistic回归分析，是一种广义的线性回归分析模型，属于机器学习中的监督学习。其推导过程与计算方式类似于回归的过程，但实际上主要是用来解决二分类问题（也可以解决多分类问题）。

逻辑回归的输入就是线性回归的输出，

$y=w_{0}+w_{1}x_{1}+w_{2}x_{2}+...+w_{n}x_{n}$ $+\eta$

找到一个线性模型进行预测，可是进行分类我们需要预测的概率，于是引入了激活函数将预测结果转换为概率

激活函数

Sigmoid 函数，也称为 Logistic 函数，是一个常用的激活函数，用于将输入映射到一个取值范围在0和1之间的输出。

$g\left ( x \right )=\frac{1}{1+e^{-x}}$

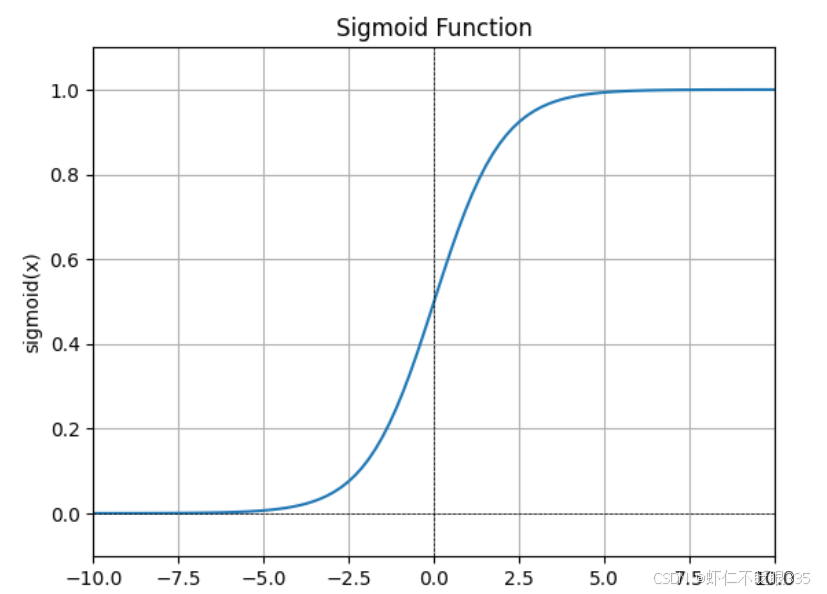
sigmoid激活函数的作用

映射到概率值：逻辑回归的目标是预测样本属于某个类别的概率。通过 Sigmoid 函数，将线性回归模型的输出映射到0和1之间的概率值，方便进行分类判断。
可解释性：Sigmoid 函数的输出在0和1之间，可以被解释为样本属于某个类别的概率。例如，输出为0.8表示属于某个类别的概率为80%，输出为0.3表示属于该类别的概率为30%。
阈值确定：根据 Sigmoid 函数的输出概率，我们可以设定一个阈值（通常是0.5），将概率大于等于阈值的样本划分为一个类别，概率小于阈值的样本划分为另一个类别。
平滑性：Sigmoid 函数的输出具有平滑性质，梯度变化较为连续，有利于使用梯度下降等优化算法对模型参数进行更新和优化。

损失函数

综上，逻辑回归的损失函数（交叉熵损失函数）：

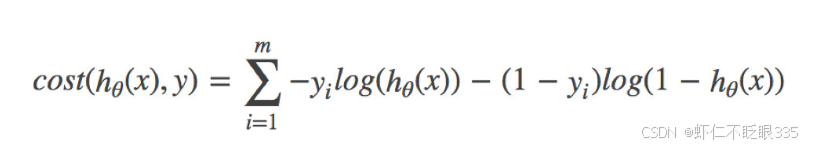
使用梯度下降的方式找到损失函数的最小值

机器学习常见回归算法

线性回归

假设标签y与特征x呈线性关系，且特征之间相互独立，寻找一条最佳直线去拟合数据。

$\eta$ 为实际生活中可能包含的噪声

$w$ 为每个特征对应的权重

$y=w_{0}+w_{1}x_{1}+w_{2}x_{2}+...+w_{n}x_{n}$ $+\eta$

这里以一元线性回归为例

如图，Y1和Y2都拟合数据，那么那条直线更好呢，这里我们引入损失函数

损失函数能够量化目标的实际值与预测值之间的差距，通常选择非负数作为损失，且数值越小表示损失越小。

残差：

残差是真实值与预测值的差值，残差越小，拟合效果越好

平方差损失函数

预测点的真实值与预测值相减，再平方（这里为了消除负值），最后进行求和，就得到了整个数据的残差。就是最常用的平方差损失函数SSE（sum of Squares for Error）

将y=wx+b代入，得到了一个关于w和b的函数，最后目的是求得Q最小时对应得 $w_{0}$ 与 $w_{1}$ $Q=\sum \left ( y_{i} - \bar{y}_{i} \right )^{2}=\sum \left ( y_{i} -\left ( \bar{w}_{0}+\bar{w}_{1} x_{i}\right ) \right )^{2}$

由于有两个未知的参数 $w_{0}$ , $w_{1}$ ,所以Q的图像是一个二维的凸函数

梯度下降（gradient descent）：

它的主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。就是找到给定点的梯度，然后朝着梯度相反的方向，就能让函数值下降的最快，所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值。

人们常常使用梯度下降的方式找到Q的最小值，当然，也可以直接求导求得最小值

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。