数学规划模型总结(附MatLab代码)
概述
定义
数学规划是统筹学的一个分支,用来研究:在给定条件下(约束条件),如何按照某一行衡量指标(目标函数)来寻求计划、管理工作中的最优方案。
通俗的讲,就是求 目标函数 在一定 约束条件 下的极值问题。
一般形式
-
min(或max):z = f(x)
-
x:决策变量(一般有多个自变量)
-
f(x):目标函数
-
不等式约束、等式约束、整数约束:约束条件
分类
- 线性规划
- 非线性规划
- 整数规划
- 0-1规划
线性规划(linear programming)
目标函数f(x) 和 约束条件均是决策变量的线性表达式。
[x fval] = linprog(c, A, b, Aeq, beq, lb,ub, x0)
% X是向量[x1,x2,...xn]' , 即决策变量。(列向量)
% fval 为 function value。
% c是目标函数的系数向量(列向量)
% A是线性不等式约束 Ax<=b 的系数矩阵,b是线性不等式约束 Ax<=b 的常数项(列向量)
% Aeq是线性等式约束 Aeq*x = beq 的系数矩阵,beq是线性等式约束 Aeq*x=beq 的常数项
% lb是X的下限,ub是X的上限。(列向量)
% x0为迭代的初始值(一般不用给)。
注:linprog函数 只能求解最小值问题,最大值问题要在目标函数前加负号,转化为最小值问题,将结果 fval = - fval 即可。
非线性规划(nonlinear programming)
目标函数f(x) 和 约束条件中存在决策变量的非线性表达式。
注:解决起来比线性规划困难,目前没有通用的算法,大多数算法都是在选定决策变量的初始之后通过一定的收索方法寻求最优的决策变量。
[x,fval] = fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)
% x0表示给定的初始值(用行向量或者列向量表示),必须得写
% A b表示线性不等式约束
% Aeq beq 表示线性等式约束
% lb ub 表示上下界约束 lb表示下界 ub表示上界
% @fun表示目标函数
function f = fun1(x)
f = -x(1)^2-x(2)^2 +x(1)*x(2)+2*x(1)+5*x(2);
end
% 这里的f实际上就是目标函数,函数的返回值也是f
% 输入值x实际上就是决策变量,由x1和x2组成的向量
% @nonlfun表示非线性约束的函数
function [c, ceq] = mynonlfun1(x)
c = [(x(1)-1)^2 - x(2)]; % 默认非线性不等式约束为 ≤ 0
ceq = [x(1)^2 - x(2)]; % 默认非线性等式约束为 = 0
end
% option 表示求解非线性规划使用的方法
% 使用interior point算法 (内点法)
option = optimoptions('fmincon','Algorithm','interior-point')
% 使用SQP算法 (序列二次规划法)
option = optimoptions('fmincon','Algorithm','sqp')
% 使用active set算法 (有效集法)
option = optimoptions('fmincon','Algorithm','active-set')
% 使用trust region reflective (信赖域反射算法)
option = optimoptions('fmincon','Algorithm','trust-region-reflective')
整数规划(integer programming)
存在变量要求取整数值的数学规则,分为 线性整数规划 和 非线性整数规划 。
注:目前所流行的求解整数规划的算法往往只适用于线性整数规划。
[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
% Matlab线性整数规划求解
% intcon 参数可以指定哪些决策变量是整数(行向量)。
0-1规划(0-1 programming)
整数规划的特例,整数变量的取值只能为0和1。
[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
% 仍然使用线性整数规划的 intlinprog 函数,只不过在lb和ub上做文章。
% 0-1变量的 lb = 0, ub = 1。
最大最小化模型
在最不利的的条件下,寻求最有利的策略。
[x,feval] = fminimax(@Fun,x0,A,b,Aeg,beg,lb,ub,@nonlfun,option)
max(feval)
% 目标函数 Fun 用一个函数向量表示
% 其他变量与非线性规划相同
多目标规划模型
一个规划问题中有多个目标。
解决方案:对多目标函数进行加权组合将问题变为单目标规划。
[x fval] = linprog(c, A, b, Aeq, beq, lb,ub, x0)
% 仍然使用线性规划的 linprog 函数
% c 中系数乘上了相应权重,并除以某一个常数(做标准化)
注:
- 多个目标函数统一为最大化或最小化问题后才可以进行加权组合。
- 如果目标函数量纲不相同,则需要对其进行标准化后再进行加权。标准化的方法一般是由目标函数除以某一个常数,该常数是指目标函数某个取值具体取值可根据经验确定。
- 对多目标函数进行加权求和时,权重需要由该问题领域的专家给定。实际建模比赛中若无特殊要求我们可另权重相同。
敏感性分析(对权重)
通过逐一改变相关变量数值的方法来解释关键指标受这些因素变动影响大小规律。
多目标规划+敏感性分析举例

%% 多目标规划
w1 = 0.4; w2 = 0.6; % 两个目标函数的权重 x1 = 5 x2 = 2
% w1 = 0.5; w2 = 0.5; % 两个目标函数的权重 x1 = 5 x2 = 2
% w1 = 0.3; w2 = 0.7; % 两个目标函数的权重 x1 = 1 x2 = 6
c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3]; % 线性规划目标函数的系数
A = [-1 -1]; b = -7; % 不等式约束
lb = [0 0]'; ub = [5 6]'; % 上下界
[x,fval] = linprog(c,A,b,[],[],lb,ub) % 求解线性规划时使用 —— 目标函数和约束条件都是线性的
f1 = 2*x(1)+5*x(2)
f2 = 0.4*x(1) + 0.3*x(2)
%% 敏感性分析
clear;clc
W1 = 0.1:0.001:0.5; W2 = 1- W1;
n =length(W1);
F1 = zeros(n,1); F2 = zeros(n,1); X1 = zeros(n,1); X2 = zeros(n,1); FVAL = zeros(n,1);
A = [-1 -1]; b = -7; % 不等式约束
lb = [0 0]; ub = [5 6]; % 上下界
for i = 1:n
w1 = W1(i); w2 = W2(i);
c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3]; % 线性规划目标函数的系数
[x,fval] = linprog(c,A,b,[],[],lb,ub);
F1(i) = 2*x(1)+5*x(2);
F2(i) = 0.4*x(1) + 0.3*x(2);
X1(i) = x(1);
X2(i) = x(2);
FVAL(i) = fval;
end
% 「Matlab」“LaTex字符汇总”讲解:https://blog.youkuaiyun.com/Robot_Starscream/article/details/89386748
% 在图上可以加上数据游标,按住Alt加鼠标左键可以设置多个数据游标出来。
figure(1)
plot(W1,F1,W1,F2)
xlabel('f_{1}的权重')
ylabel('f_{1}和f_{2}的取值')
legend('f_{1}','f_{2}')
figure(2)
plot(W1,X1,W1,X2)
xlabel('f_{1}的权重')
ylabel('x_{1}和x_{2}的取值')
legend('x_{1}','x_{2}')
figure(3)
plot(W1,FVAL) % 看起来是两个直线组合起来的下半部分
xlabel('f_{1}的权重')
ylabel('综合指标的值')
典型例题
例题一:护士排班问题
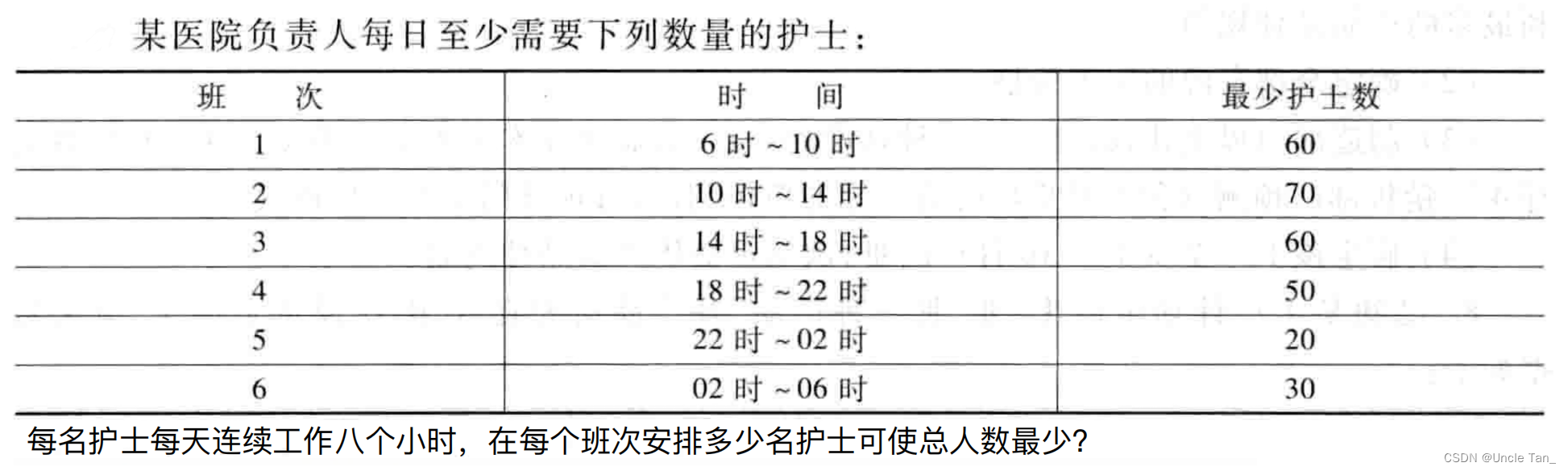
MatLab代码
%% 分析问题为 整数规划 问题
clear;clc
c = ones(6,1);
intcon = 1:6;
A = -[ 1 0 0 0 0 1;
1 1 0 0 0 0;
0 1 1 0 0 0;
0 0 1 1 0 0;
0 0 0 1 1 0;
0 0 0 0 1 1 ];
b = -[60; 70; 60; 50; 20; 30];
lb = zeros(6, 1);
[x,fval] = intlinprog(c,intcon,A,b,[],[],lb);
disp('班次安排:');
disp(x');
disp([ '护士总数:',num2str(fval)]);
MatLab输出
班次安排:
60 10 50 0 30 0
护士总数:150
例题二:货机装货问题
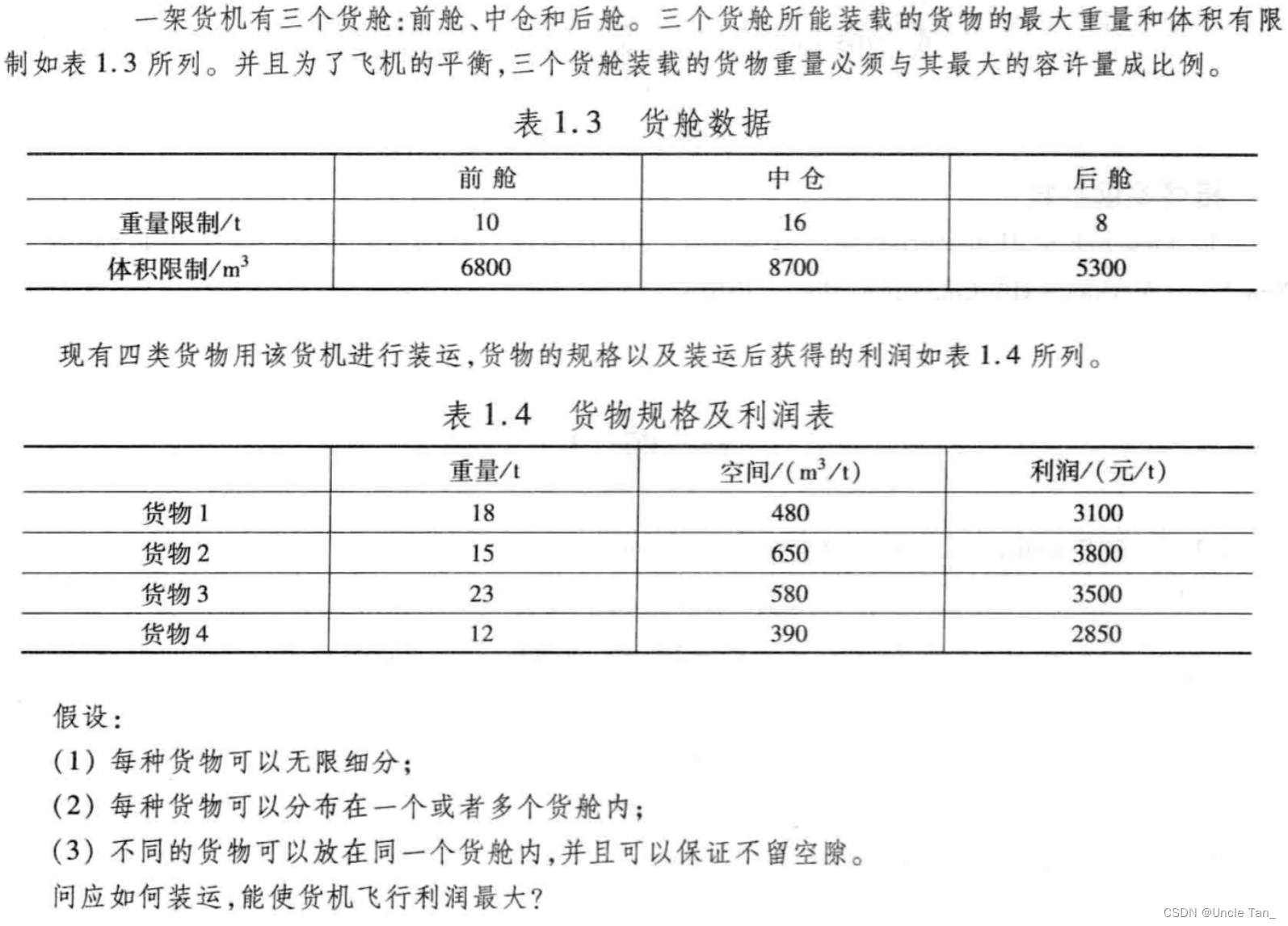
MatLab代码
%% 分析问题为 线性规划 问题
% 决策变量:xij为将第i个货物装到第j个舱里的吨数;
% 转化前:x11 x12 x13 x21 x22 …… x42 x43
% 转化后:x1 x2 x3 x4 x5 …… x11 x12
% 二维变量一维化,方便后续处理
% 货舱体积限制的线性不等式约束
clear;clc
format long g %可以将Matlab的计算结果显示为一般的长数字格式(默认会保留四位小数,或使用科学计数法)
A_v = [ eye(3) * 480 eye(3) * 650 eye(3) * 580 eye(3) * 390]; % eye(n) 表示生成n*n的单位阵
b_v = [ 6800; 8700; 5300];
% 货舱重量限制的线性不等式约束
A_w1 = [ eye(3) eye(3) eye(3) eye(3)];
b_w1 = [ 10; 16; 18];
% 货物重量限制的线性不等式约束
A_w2 = [ ones(1, 3) zeros(1, 9);
zeros(1, 3) ones(1, 3) zeros(1, 6);
zeros(1, 6) ones(1, 3) zeros(1, 3);
zeros(1, 9) ones(1, 3)];
b_w2 = [ 18; 15; 23; 12];
% 汇总线性不等式约束
A = [A_v; A_w1; A_w2];
b = [b_v; b_w1; b_w2];
% 每个货舱装载物比例等式约束
Aeq_1 = repmat([1 0 0], 1, 4) / 10 - repmat([0 1 0], 1, 4) / 16; % 货舱一和货舱二重量成比例
Aeq_2 = repmat([1 0 0], 1, 4) / 10 - repmat([0 0 1], 1, 4) / 8; % 货舱一和货舱三重量成比例
Aeq = [Aeq_1; Aeq_2];
beq = zeros(2, 1)
% 计算飞机利润的系数矩阵
c = -[ones(3, 1) * 3100; ones(3, 1) * 3800; ones(3, 1) * 3500; ones(3, 1) * 2850];
% 每次装运最小值为0
lb = zeros(12, 1);
[x, fval] = linprog(c, A, b, Aeq, beq, lb);
fval = -fval;
% 对 x 做变形转置处理,输出结果
x = reshape(x, 3, 4)';
disp('装运方式:(行为货物,列为货舱)');
disp(x);
disp(['最大飞行利润', num2str(fval)]);
MatLab输出
装运方式:(行为货物,列为货舱)
0 0 0
10 0 5
0 12.9473684210526 3
0 3.05263157894737 0
最大飞行利润121515.7895
例题三:非线性规划最值问题

MatLab代码
%% mainCode部分
clc;clear
format long g %可以将Matlab的计算结果显示为一般的长数字格式(默认会保留四位小数,或使用科学计数法)
% 给定初始值,此处可以使用蒙特卡洛模拟给定初始值。
x0 = [1 1 1];
% 线性不等式约束
A = [-1 -2 0];
b = 1;
% 决策变量范围约束
lb = [0 -inf -inf];
% 调用函数求解
[x,fval] = fmincon(@fun,x0,A,b,[],[],lb,[],@nonlfun);
fval = -fval
%% fun函数部分
function f = fun(x)
f = 2 * x(1) + 3 * x(1)^2 + 3 * x(2) + x(2)^2 + x(3);
f = -f; % 最大值问题转化为最小值问题
end
%% nonlfun函数部分
function [c, ceq] = nonlfun(x)
% 非线性不等式约束
c = [x(1) + 2 * x(1)^2 + x(2) + 2 * x(2)^2 + x(3) - 10;
x(1) + x(1)^2 + x(2) + x(2)^2 - x(3) - 50;
2 * x(1) + x(1)^2 + 2 * x(2) + x(3) - 40;];
% 非线性等式约束
ceq = x(1)^2 + x(3) - 2;
end
MatLab输出
x =
2.33333286682278 0.166667730107356 -3.44444226075484
fval =
18.0833315976581
例题四:覆盖问题

MatLab代码
%% 分析问题为 0-1规划 问题
clc;clear
c = ones(6, 1); % 目标函数的系数矩阵
intcon = (1:6); % 整数的位置为1-6
% 保证每一个小区被覆盖的次数 ≥ 1
A = -[1 1 1 0 0 0; % 只有B1 B2 B3 能覆盖A1
0 1 0 1 0 0;
0 0 1 0 1 0;
0 0 0 1 0 1;
1 1 1 0 0 0;
0 0 0 0 1 1;
1 0 0 0 0 0;
0 1 0 1 0 1;];
b = -ones(8, 1);
% 通过上下限,构建 0-1 分布
lb = zeros(6, 1);
ub = ones(6, 1);
% 调用intlinprog()函数求最优解
[x,fval] = intlinprog(c,intcon,A,b,[],[],lb,ub);
disp('建校方案为:');
for i = 1:6
if(x(i)) == 1
disp(['B', num2str(i)]);
end
end
disp([ '最小建校地址数目:', num2str(fval)]);
MatLab输出
建校方案为:
B1
B4
B5
最小建校地址数目:3


























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










