CF771 C. Inversion Graph(并查集)

最新推荐文章于 2025-08-05 13:20:24 发布

原创最新推荐文章于 2025-08-05 13:20:24 发布 · 546 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

codeforces 专栏收录该内容

31 篇文章

订阅专栏

本文介绍如何使用并查集算法来找出给定数字序列中，前后数字大小关系满足条件（前大后小）时，形成的无边数字集合数量。通过维护最大值数组a和最小值数组b，快速判断是否可以合并集合，从而得到答案。

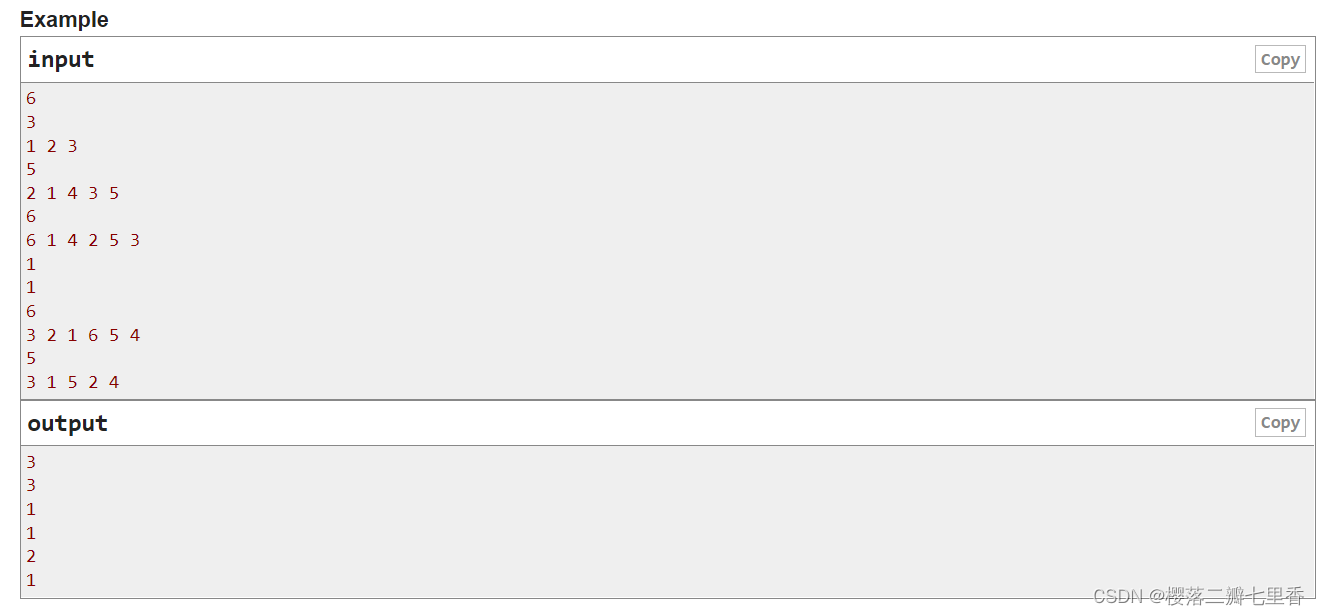
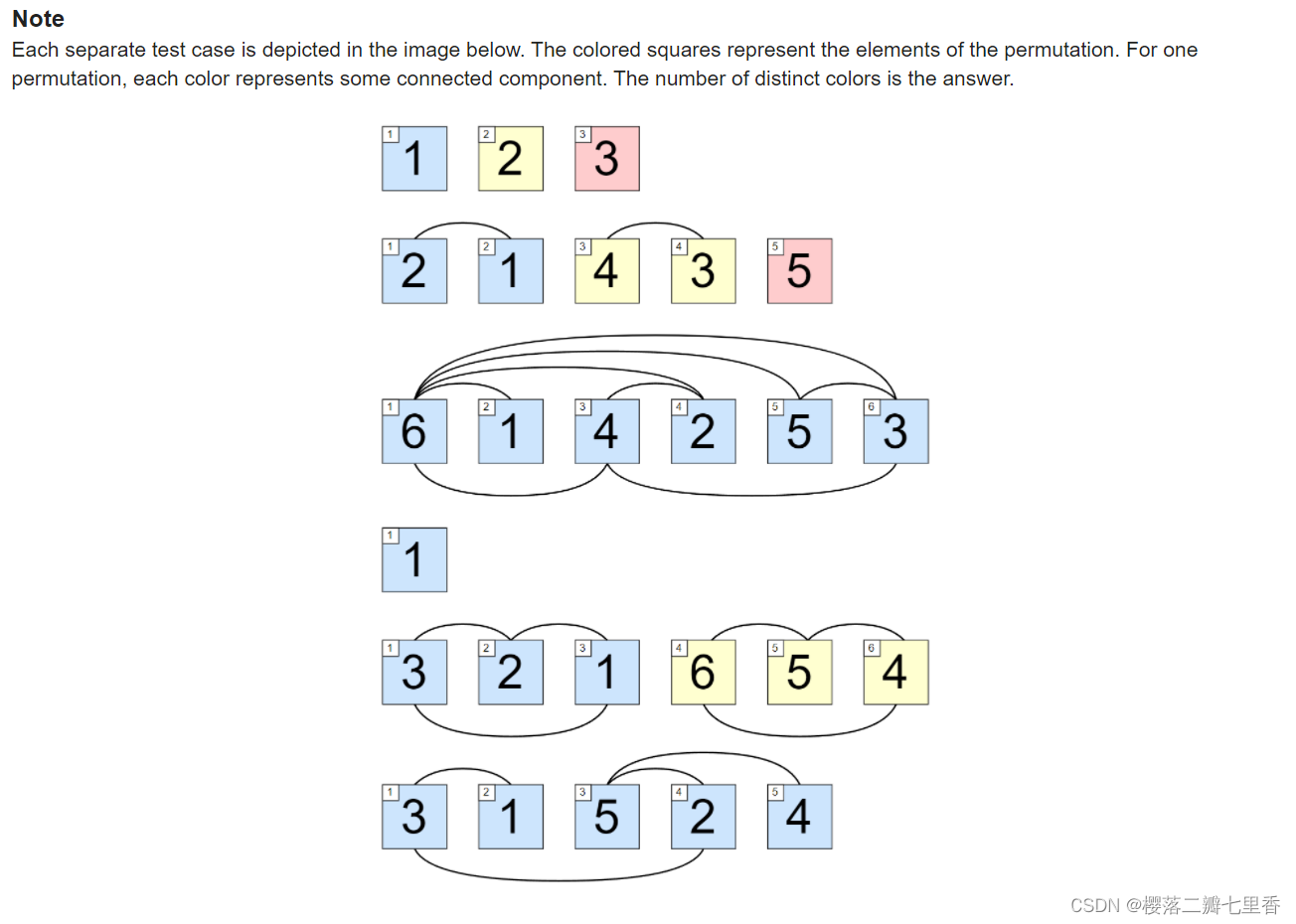
题意分析 : 对于每个数字, 若前面的数字大于后面的数字, 则在这两个数字之间连一条边, 要求没有边连着的数字集合个数

思路 : 可以很容易的想到用并查集的思想, 用一个数组a[i]记录1到i的最大值, b[j]记录j到n的最小值, 当a[i]<b[j+1] 时(前面集合中的最大值, 小于后面集合的最小值), 可以将两个集合合并, 即并查集记录的是一个满足题意数字集合, 通过a[i]和b[j]来进行维护

代码如下:

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
using namespace std;

const int N = 1e5+10;

int a[N], b[N];

int main()
{
    int T;
    scanf("%d", &T);
    while(T -- )
    {
        int n;
        scanf("%d", &n);
        for(int i = 1; i<=n; i++)
        {
            scanf("%d", &a[i]);
            b[i] = a[i];
        }
        for(int i = 2, j = n-1; i<=n; i++, j--)
        {
            a[i] = max(a[i], a[i-1]); // a[i] 记录1到i的最大值
            b[j] = min(b[j], b[j+1]); // b[j] 记录j到n的最小值
        }
        int ans = 1;
        // 遍历所有值, 当前面的最大值大于后面的最小值就可以合并, 反之,就不能合并, 集合+1
        // 如样例2 1 4 3 5
        // i = 1, 前面的最大值为2, 后面的最小值为1,可以合并
        // i = 2, 前面的最大值为2, 后面的最小值为3, 不能合并, ans++ 
        // i = 3, 前面的最大值为4, 后面的最小值为3, 可以合并
        // i = 4. 前面的最大值为4, 后面的最小值为5, 不能合并, ans++
        // 最终ans = 3;
        for(int i = 1; i<n; i++)
        {
            if(a[i] < b[i+1]) ans++;
        }
        cout<<ans<<endl;
    }
}