opencv形态学操作

连通性

        在图像中，最⼩的单位是像素，每个像素周围有8个邻接像素，常⻅的邻接关系有3 种：4邻接、8邻接和D邻接。分别如下图所示：

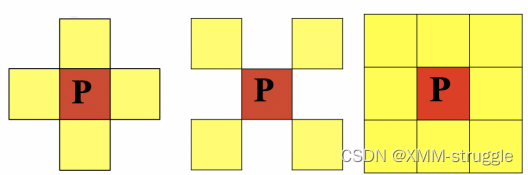
        4邻接：像素p(x,y)的4邻域是：(x+1,y)；(x-1,y)；(x,y+1)；(x,y-1)，⽤N (p)表示像素p的4邻接 D邻接

        像素p(x,y)的D邻域是：对⻆上的点 (x+1,y+1)；(x+1,y-1)；(x1,y+1)；(x-1,y-1)，⽤N (p)表示像素p的D邻域

        8邻接：像素p(x,y)的8邻域是： 4邻域的点 ＋ D邻域的点，⽤N (p)表示像素p 的8邻域

连通性是描述区域和边界的重要概念，两个像素连通的两个必要条件是：

        1. 两个像素的位置是否相邻

        2. 两个像素的灰度值是否满⾜特定的相 似性准则（或者是否相等 根据连通性的定义，有4联通、8联通和m联通三种。

                4联通：对于具有值V 的像素p和q，如果q在集合N (p)中，则称这两个像素是4 连通。

                8联通：对于具有值V 的像素p和q，如果q在集 合N (p)中，则称这两个像素是8 连通。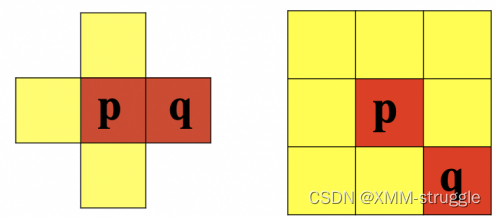

          对于具有值V 的像素p和q，如果: q在集合N (p)中，或 q在集合N (p)中，并且N (p)与N (q)的交集为空（没有值V 的像素） 则称这两个像素是m连通的，即4连通和D连通的混合连通。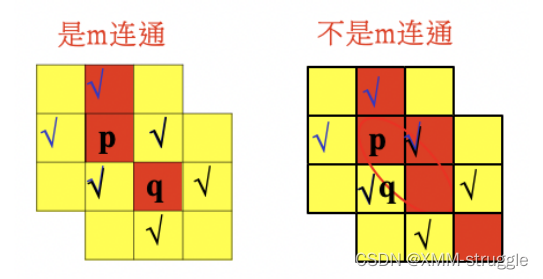

 形态学操作

        形态学转换是基于图像形状的⼀些简单操作。它通常在⼆进制图像上执⾏。腐蚀和 膨胀是两个基本的形态学运算符。然后它的变体形式如开运算，闭运算，礼帽⿊帽 等。

腐蚀和膨胀

        腐蚀和膨胀是最基本的形态学操作，腐蚀和膨胀都是针对⽩⾊部分（⾼亮部分）⽽⾔的。

                膨胀就是使图像中⾼亮部分扩张，效果图拥有⽐原图更⼤的⾼亮区域；腐蚀是原图 中的⾼亮区域被蚕⻝，效果图拥有⽐原图更⼩的⾼亮区域。膨胀是求局部最⼤值的 操作，腐蚀是求局部最⼩值的操作。

        1. 腐蚀具体操作是：⽤⼀个结构元素扫描图像中的每⼀个像素，⽤结构元素中的每⼀ 个像素与其覆盖的像素做“与”操作，如果都为1，则该像素为1，否则为0。如 下图所示，结构A被结构B腐蚀后：

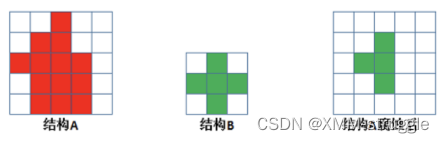        腐蚀的作⽤是消除物体边界点，使⽬标缩⼩，可以消除⼩于结构元素的噪声点。

cv.erode(img,kernel,iterations)

参数：

        img: 要处理的图像

        kernel: 核结构

        iterations: 腐蚀的次数，默认是1

        1. 膨胀具体操作是：⽤⼀个结构元素扫描图像中的每⼀个像素，⽤结构元素中的每⼀个像 素与其覆盖的像素做“与”操作，如果都为0，则该像素为0，否则为1。如下图所 示，结构A被结构B腐蚀后：

         

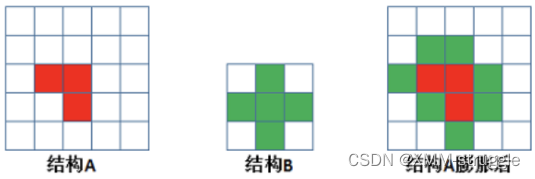
        膨胀的作⽤是将与物体接触的所有背景点合并到物体中，使⽬标增⼤，可添补⽬标 中的孔洞。

cv.dilate(img,kernel,iterations) 

参数：

        img: 要处理的图像

        kernel: 核结构

        iterations: 腐蚀的次数，默认是1

示例

我们使⽤⼀个5*5的卷积核实现腐蚀和膨胀的运算：

import cv2 as cv
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] # 指定默认字体：解决plot不能显示中文问题
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

# 1. 读取图⽚
img = cv.imread("E:/m.jpg")
# 2 创建核结构
kernel = np.ones((5, 5), np.uint8)
# 3 图像腐蚀和膨胀
erosion = cv.erode(img, kernel) # 腐蚀
dilate = cv.dilate(img,kernel) # 膨胀
# 4 图像展示
fig,axes=plt.subplots(nrows=1,ncols=3,figsize=(10,8),dpi=100)
axes[0].imshow(img)
axes[0].set_title("原图")
axes[1].imshow(erosion)
axes[1].set_title("腐蚀后结果")
axes[2].imshow(dilate)
axes[2].set_title("膨胀后结果")
plt.show()

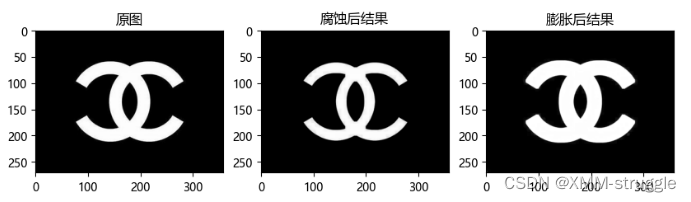
 开闭运算

        开运算和闭运算是将腐蚀和膨胀按照⼀定的次序进⾏处理。 但这两者并不是可逆 的，即先开后闭并不能得到原来的图像。

        1. 开运算

                开运算是先腐蚀后膨胀，其作⽤是：分离物体，消除⼩区域。特点：消除噪 点，去除⼩的⼲扰块，⽽不影响原来的图像。

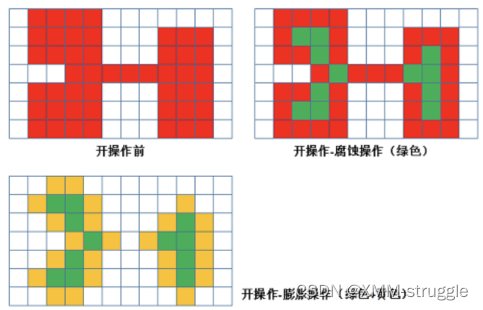
         2. 闭运算

                闭运算与开运算相反，是先膨胀后腐蚀，作⽤是消除/“闭合”物体⾥⾯的孔洞， 特点：可以填充闭合区域。

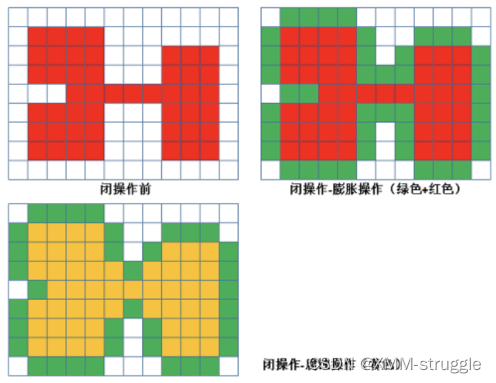
cv.morphologyEx(img, op, kernel)

参数：

        img: 要处理的图像

        op: 处理⽅式：若进⾏开运算，则设为cv.MORPH_OPEN，若进⾏闭运 算，则设为cv.MORPH_CLOSE

        Kernel： 核结构

示例

        使⽤10*10的核结构对卷积进⾏开闭运算的实现。

import cv2 as cv
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] # 指定默认字体：解决plot不能显示中文问题
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

# 1. 读取图⽚
img1 = cv.imread("E:/m.jpg")
img2 = cv.imread("E:/m.jpg")
# 2 创建核结构
kernel = np.ones((10, 10), np.uint8)
# 3 图像的开闭运算
cvOpen = cv.morphologyEx(img1,cv.MORPH_OPEN,kernel) # 开运算
cvClose = cv.morphologyEx(img2,cv.MORPH_CLOSE,kernel)# 闭运算
# 4 图像展示
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(10,8))
axes[0,0].imshow(img1)
axes[0,0].set_title("原图")
axes[0,1].imshow(cvOpen)
axes[0,1].set_title("开运算结果")
axes[1,0].imshow(img2)
axes[1,0].set_title("原图")
axes[1,1].imshow(cvClose)
axes[1,1].set_title("闭运算结果")
plt.show()

礼帽和⿊帽

1. 礼帽运算

        原图像与“开运算“的结果图之差，如下式计算：

        因为开运算带来的结果是放⼤了裂缝或者局部低亮度的区域，因此，从原 图中减去开运算后的图，得到的效果图突出了⽐原图轮廓周围的区域更明亮的 区域，且这⼀操作和选择的核的⼤⼩相关。

        礼帽运算⽤来分离⽐邻近点亮⼀些的斑块。当⼀幅图像具有⼤幅的背景的 时候，⽽微⼩物品⽐较有规律的情况下，可以使⽤顶帽运算进⾏背景提取。

2. ⿊帽运算

        为”闭运算“的结果图与原图像之差。数学表达式为：

        ⿊帽运算后的效果图突出了⽐原图轮廓周围的区域更暗的区域，且这⼀操作和 选择的核的⼤⼩相关。

        ⿊帽运算⽤来分离⽐邻近点暗⼀些的斑块。

cv.morphologyEx(img, op, kernel) 

参数：

        img: 要处理的图像

        op: 处理⽅式：

        Kernel： 核结构

示例

 

import cv2 as cv
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] # 指定默认字体：解决plot不能显示中文问题
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

# 1. 读取图⽚
img1 = cv.imread("E:/m.jpg")
img2 = cv.imread("E:/m.jpg")
# 2 创建核结构
kernel = np.ones((10, 10), np.uint8)
# 3 图像的礼帽和⿊帽运算
cvOpen = cv.morphologyEx(img1,cv.MORPH_TOPHAT,kernel) # 礼帽运算
cvClose = cv.morphologyEx(img2,cv.MORPH_BLACKHAT,kernel)# ⿊帽运算
# 4 图像显示
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(10,8))
axes[0,0].imshow(img1)
axes[0,0].set_title("原图")
axes[0,1].imshow(cvOpen)
axes[0,1].set_title("礼帽运算结果")
axes[1,0].imshow(img2)
axes[1,0].set_title("原图")
axes[1,1].imshow(cvClose)
axes[1,1].set_title("⿊帽运算结果")
plt.show()