【C++算法】全排列

问题

设计⼀个递归算法⽣成 n 个元素{r1,r2,…,rn}的全排列。任意输⼊⼀串整数或字符，输出结果能够⽤递归⽅法实现整数或字符的全排列。

分析

首先题目的要求是我们输入的一串字符或数字能够通过递归输出其全排列的所有情况，所以关键就是在如何递归实现全排列。

       本项目采用的方法如下

思路就是让一个未被确定顺序的数组里面的每一个元素都放在最前面一次。

比如134，就先让1在最前面一次，然后剩下的34，就先让3在前面形成134，再让4在前面形成143，这样就完成了第一次循环，然后第二次循环到3在最前面，剩下的14，就先让1在前面形成314，再让4在前面形成341，以此类推。

所以递归思路如下：关键就是让所有的元素都在下标为0，1，2……n的位置上呆过一次，所以这里每次递归的时候都让初始点往后移一位，这样每次递归的时候都可以让初始点后面的所有元素都换到不同初始点一次，然后通过循环让初始点后的所有元素都换来初始点一次，递归终止条件就是直到最后一个元素也被换来初始点一次了，那么这一层递归就结束了。

需要注意的点：

1.只要让一个元素和后面的元素交换就可以了，不要让他和前面的元素交换，因为比如134，13交换和31交换其实是一样的，也就是说在1的时候就已经和3交换过了，到3的时候就不需要再和1交换了。

2.注意回溯，要保证每个元素都当一次排头，所以要保证选择排头的时候数组为原样，这样才能按照循环1234分别选择排头，不然可能会出现一个元素多次当排头的情况，比如134，则让134分别当排头的时候要保证数组每次都是134不能为其他形式，不然就会变成134的时候选择第一个元素1为排头，后面交换13变成314，然后第二次循环选择第二个元素还是1当排头。

因此实现代码如下：

#include <bits/stdc++.h>
using namespace std;

string str;
int n;

void permutation(int k) //k表示从哪里开始与后面的交换
{
	if (k == n) 
	{
		cout << str << endl;
	}
	for (int i = k;i < n;i++) //k-n代表未被确定顺序的数组元素下标
	{
		swap(str[k], str[i]);  //让k-n的每一个元素都在最前面一次
		permutation(k + 1);  //下一个数组
		swap(str[i], str[k]);  //回溯，因为要保持原样才能保证每个元素都在最前面一次
	}
}

int main() {
	cin >> str;
	n = str.size();
	permutation(0);
	return 0;
}

运行结果如下：

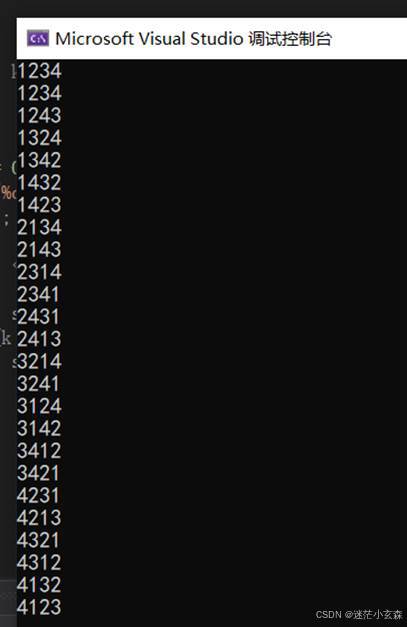
        全排列的递归实现，实际上就是让数组内的每个元素都在数组内的每个位置上呆一次，所以通过递归，每次递归的时候都让后面的元素通过循环换到此层递归表示的初始点位置上来，以此达到全排列的效果。需要注意的点有两个：一个是交换元素的时候只让初始点的元素和后面的元素交换，不要和初始点前面的元素交换；另一个是需要进行回溯，保证每次交换的时候数组保持初始状态不变，不能是进行过交换的状态。