机器学习-线性回归

醉翁之意不在酒~

已于 2023-07-19 14:55:24 修改

阅读量1.3k

点赞数 3

分类专栏：机器学习文章标签：机器学习线性回归回归

于 2022-01-07 20:08:24 首次发布

LBWNB

本文链接：https://blog.youkuaiyun.com/qq_58535145/article/details/122362741

版权

机器学习专栏收录该内容

15 篇文章

订阅专栏

一、回归算法

• 回归算法是一种有监督算法

• 回归算法是一种比较常用的机器学习算法，用于构建一个模型来做特征向量到标签的映射。在算法的学习过程中，试图寻找一个模型，最大程度拟合训练数据。

• 回归算法在使用时，接收一个n维度特征向量，输出一个连续的数据值

二、执行图

三、案例

1、此时我们有这么一组数据，如下图：

2、我们可以建立一个直角坐标系来将这些点标出如图一：（蓝色为以上给出的坐标）

图一

图二

3、由图中的蓝色线条，我们可以设置线性模型为（一元一次函数）：

4、我们的目的是通过算法去找到最优的一条线能尽可能拟合所有点，我们的参数如果发生变化那么我们的蓝线（或绿线）也会随之变化，比如图一和图二我们不难看出图一的效果更佳，但我们是如何去判断蓝线在什么时候最好呢（我们要使用代价函数后文会详细讲解），以及我们的参数该怎么养确定才会得到最好的拟合线？

5、这时我们需要用到最小二乘法、正规方程法、梯度下降法

四、最小二乘法

已知损失函数J(a,b)：

分别关于a和b对J(a,b)求偏导，并令其为零解出a和b。这里直接给出结果：

==》

接下来详细介绍梯度下降

3、案例（接上文）

其中数据集既是我们我们所有的点，

实际值就是每个点的纵坐标值，

估计值就是每个点与x轴做垂线其与蓝线的交点的纵坐标值（即把点的横坐标带入到线性模型中所得到的h(x)的值），

估计误差就是每个点的实际值减去估计值，

代价函数的目的就是求出所有点产生出误差的均值（越小越好），由公式可知代价函数为一个二次函数，图像大致为V字型。

4、代价函数的解释

现在我们假设有3个点分别为：（1,1）、（2,2）、（3,3）

代价函数为：

首先我们假设一个函数为：h(x) = x,我们可以计算出其代价函数值（如图）：

第二次我们假设函数为：h(x)=0.5x,计算结果如图（其中m为点的个数）：

第三次我们假设函数为：h(x) = 2x,计算结果如下图：

我们已经知道我们的代价函数的值越小那么误差就越小，所以我们需要的是找到一个极值点使得代价函数的值最小，由下图我们不难看出在x=1时代价函数会取得最小值（对应h(x)=x此时完全拟合没有误差），我们继续观察代价函数的图像，发现在x=1出对代价函数求导（即切线），我们可以得出它在x=1处的倒数值为0，那么问题来了我们怎么样才能在每一个线性问题中去找到这个倒数为0的情况呢（即找到模型的最优解）？

因此我们要引入梯度下降，来解决这一问题。

五、梯度下降

1、梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数J(θ0,θ1) 的最小值。梯度下降背后的思想是：开始时我们随机选择一个参数的组合（θ0,θ1），计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。

2、在梯度下降中我们会设置一个学习率α（learning rate），大于0的一个很小经验值，它决定沿着能让代价函数下降的程度有多大。

我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数，由此来更新你的θ值

其中△θj为代价函数对θj的偏倒数

θj为需要更新的参数

把代价函数拿过来方便我们观察：

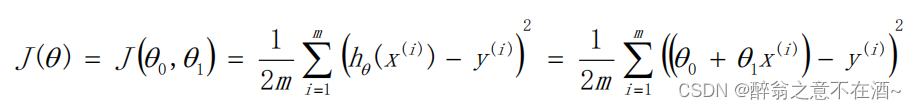
这样看可能不是特别好理解具体是如何更新参数值，所以接下来我会举出详细的例子来助于大家跟好的去理解这个做法。

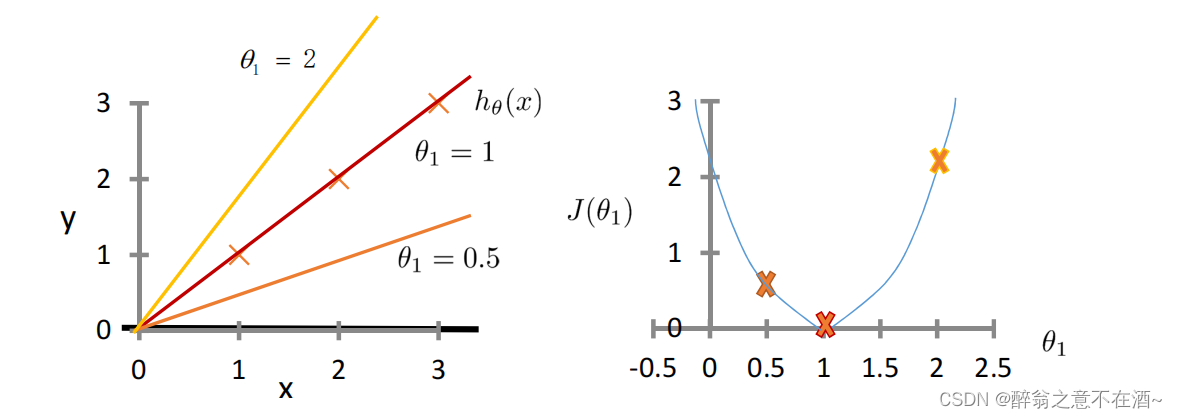
首先我们看上图，假设我们现在所求出来的函数为θ=2（y=2x）这条曲线，他在代价函数中所对应的点为右上侧的点，接下来我们对这个点使用这个公式：

这个公式的意思就是求出这个点在代价函数上的倒数，显而易见这个倒数是个正数。接线来我们要使用这个公式：

我们已知θj=2（偏大），现在这个公式表示的是：θj = 2 - α△θj，α（学习率）是一个大于0的很小的值，比如我们设置α=0.01，那么我们的θj就会慢慢变小，逐渐接近我们的最优解（θ=1，也就是y=x这条线）。

上面是倒数为正的情况，接下来我们看看当一个点的倒数为负时的情况。

我们选取θ=0.5（y=0.5x）这条线，前面所有操作不变，直到我们使用这个公式时：

我们的△θj是一个负数，此时变为θj = 0.5 + α△θj，我们同样设置α=0.01，那么我们的θj会慢慢变大，逐渐接近θ=1（也就是y=x这条线）。

但是我们会发现如果α（学习率）过小，或者过大好像也会带来不少麻烦，究竟是何种麻烦呢？我们继续向下面研究。

3、学习率对模型的影响

（1）首先是学习率太小，我们由上面的公式可以明显得到，我们迭代的速度会非常慢，一次只挪动一点，效率极低（如图）：

（2）如果学习率过大，那么我们的θ值可能会偏离和越过最优值，无法收敛（如图）：

由此可见学习率的设置非常重要！

了解到线性回归是如何来实现的后，现在我们要更深入的去了解参数更新方程（参数具体怎样更新）。

六、参数更新方程

首先我们要知道我们要更新的是2个参数θo和θ1，分别对应截距和权重，因此我们需要对2个参数求偏导：（数学推导不做讲解）（求偏导参照代价函数来求）

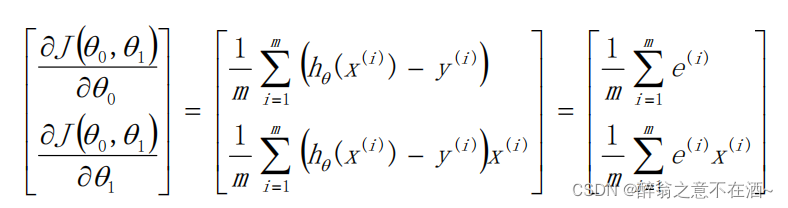其中我们设：

注意:颜色加深的为向量！

七、代码实现底层

1、首先我们导入需要用到的库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

2、我们设置两个数据x,y

x = np.array([4,3,3,4,2,2,0,1,2,5,1,2,5,1,3])
y = np.array([8,6,6,7,4,4,2,4,5,9,3,4,8,3,6])
#获取样本数量
m = len(x)
#x增加一列
x = np.c_[np.ones([m,1]),x]
print(x.shape)
#为了后续维度对应，y也做维度变化
y = y.reshape(15,1)
print(y.shape)

3、创建一个截距和权重（随机）

theta = np.zeros([2,1])
theta

4、对theta进行更新

#超参数alpha 学习率 步长
alpha = 0.01
#迭代次数
m_iter = 1000
#定义一个数组，存储所有的代价数据
for i in range(m_iter):
    y_hat = x.dot(theta) #求预测值
    error = y_hat - y    #误差值
    cost_val = 1/2 * m * error.T.dot(error) #代价值
    delta_theta = 1/m *x.T.dot(error)  #求导数
    theta = theta - delta_theta*alpha

theta

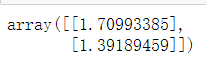
5、画出拟合曲线

plt.scatter(x[:,1],y,c='blue') #x有两列数据
plt.plot(x[:,1],y_hat,'r-')  #预测模型
plt.show()

八、正规方程法

公式如下：

直接上案例：

#把矩阵带入到公式直接计算
X = np.mat([[1,1],[2,1],[3,1],[4,1]])
Y = np.mat([[3.2],[4.7],[7.3],[8.5]])
print((X.T*X).I*X.T*Y)

调用模型计算：

from sklearn.linear_model import LinearRegression
X = np.mat([[1,1],[2,1],[3,1],[4,1]])
Y = np.mat([[3.2],[4.7],[7.3],[8.5]])
model = LinearRegression(fit_intercept=False) #调用形式，不拟合截距
model.fit(X,Y) #拟合过程，就包含梯度下降
print('参数为：',model.coef_)