论文:Si, Haonan, et al. “Environment-Aware Positioning by Leveraging Unlabeled Crowdsourcing Data.” IEEE Internet of Things Journal (2024).
标签:WiFi、
摘要
本文提出了一个新型的定位模型:environment aware positioning (ENAP), utilizing unlabeled
crowdsourcing trace data. 环境感知定位,利用无标签的众包跟踪数据。
分为一下三个步骤:①将无标签的众包跟踪数据转换为一个聚类空间;②将聚类空间映射到定位空间;③以无监督的方式不断更新定位模型
另外:①Short-term positioning: 为了提高众包用户设备异构的性能和鲁棒性,提出了一种自适应融合多信号特征的空间变换聚类方案。②Long-term positioning为了确保长期的定位稳定性和持续的环境感知能力(指的是基站的空间拓扑发生变化),我们在ENAP中加入了一个动态重放存储器(用来收集最新的环境感知信息),使定位模型能够无监督地在线更新。
1. Introduction
- 为了解决信号变化和设备异构型问题,提出了一个fusion c-means(FuCM)聚类方法,区分来自不同位置收集的信号测量值signal measurements。(融合了多个导数特征,包括RSSI, difference fingerprint (DIFF), and hyperbolic location fingerprint (HLF))
- 通过利用轨迹测量的连续性和采用calibrated multidimensional sacling(CMDS)方案,本文建立了一个从cluster spaces到positioning spaces的映射,从而确定cluster centers的位置。
- 随后,使用一个分类模型计算给定信号测量值的位置,以membership function作为权重。
2. Related works
研究现状:室内定位技术和基于众包的室内定位
3. Problem Formulation
A. Definition of Indoor Positioning
一个室内环境被多个基站覆盖。待定位目标可以采集来自这些基站的信号并测量其特征,例如RSSI、time of flight。注意:待定位目标在不同的位置采集的信号特征不一样,所以可以通过分析信号的特征来对目标进行定位。
假设有ppp个基站,那么每个位置采集的measurement可以表示成 f={f(1),f(2),…,f(p)}\mathbf{f} = \{f^{(1)}, f^{(2)}, \ldots, f^{(p)}\}f={f(1),f(2),…,f(p)},其中 f(i)f^{(i)}f(i)表示来自第iii个基站的信号。所以定位算法的目标就是使用尽可能准确的f\mathbf{f}f来估计目标的位置。
(相当于采用的是下行信号的定位方式)
B. Current Solutions
当前的室内定位方法:三边定位和指纹定位。
C. Preliminary for the Proposed ENAP
收集众包数据:收集用户随着移动轨迹的信号数据(无位置标签)。
假设收集了NTN_\mathcal{T}NT条轨迹,其中第jjj条轨迹包含了qjq_jqj 轨迹点,收集的无标签measurements数据可以表示为Tj=⟨f1,f2,…,fqj⟩\mathcal{T}_j =
\langle \mathbf{f}_1, \mathbf{f}_2, \ldots, \mathbf{f}_{q_j} \rangleTj=⟨f1,f2,…,fqj⟩。则总的轨迹数据存储可以表示为F=⟨T1,T2,…,TNT⟩\mathcal{F} = \langle \mathcal{T}_1, \mathcal{T}_2, \ldots, \mathcal{T}_{N_\mathcal{T}} \rangleF=⟨T1,T2,…,TNT⟩。
在众包数据收集过程中,受到人为干扰或相邻信号的影响,可能会出现基站消失的问题,即目标在某个位置可能收集不到来自某个基站的信号(用RSSI=100dBm表示无法检测到基站)。
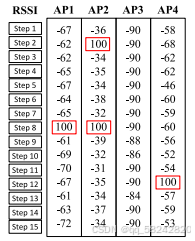
引:信号强度的单位为dBm(分贝毫瓦)。一般来说,dBm 值越大,表示信号强度越强。接近 0dBm 的数值表示非常强的信号。例如,0dBm 意味着信号强度为 1 毫瓦。负数的 dBm 值表示较弱的信号。例如,- 30dBm 比 - 60dBm 的信号要强。
为了解决无法检测的基站的测量值问题,本文对数据进行了预处理。
如果来自某个基站的RSSI measurements在第i−1i-1i−1步和第i+1i+1i+1步都很高,而在第iii步没有被检测到,我们认为这种情况基站其实仍在可检测范围,只是因为某些原因被终端错过了。为了补全丢失的数据,可以采用以下的规则去处理replay memory F\mathcal{F}F:
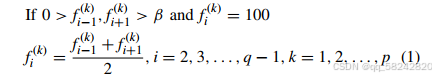
其中β\betaβ表示一个阈值参数,fi(k)f_{i}^{(k)}fi(k)表示在第iii步来自第kkk个基站的RSSI measurement。
4. Proposed algorithm
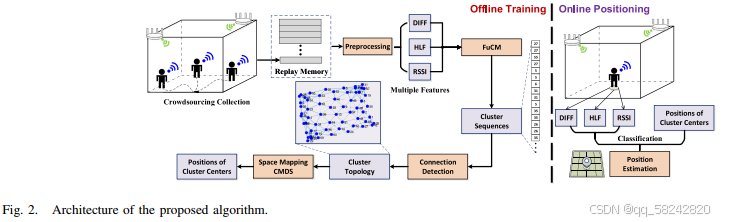
所提的ENAP如图2所示,包含以下步骤:1) FuCM clustering; 2) space mapping; 3) optimization;
4) online updates; and 5) positioning.
A. FuCM Clustering
将无标签的信号数据分类成一系列的簇clusters,聚类方案FuCM。
首先,对于一个经过预处理的measurement replay memory F=[f1,f2,…,fK]T\mathcal{F} = [\mathbf{f}_1, \mathbf{f}_2, \ldots, \mathbf{f}_K]^TF=[f1,f2,…,fK]T,定义一个c−划分空间(c−partitionspace)c-划分空间(c-partition space)c−划分空间(c−partitionspace),如下所示:
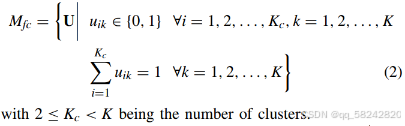
解释:
Mfc={U∣uik∈{0,1}∀i=1,2,…,Kc,k=1,2,…,K}M_{fc} = \left\{ \mathbf{U} \mid u_{ik} \in \{0,1\} \quad \forall i = 1,2,\ldots,K_{c}, k = 1,2,\ldots,K \right\}Mfc={U∣uik∈{0,1}∀i=1,2,…,Kc,k=1,2,…,K},这里的uiku_{ik}uik是一个二元变量,表示第iii个聚类是否包含第kkk个测量数据;
∑i=1Kcuik=1,∀k=1,2,…,K\sum_{i = 1}^{K_c} u_{ik}=1, \forall k = 1, 2, \ldots, K∑i=1Kcuik=1,∀k=1,2,…,K,这意味着每个测量数据fk\mathbf{f}_kfk只能属于其中一个聚类;
2≤Kc<K2 \leq K_c < K2≤Kc<K,其中KcK_cKc表示聚类的数量,它至少为2且小于总的测量数据数量KKK。
c-means函数的定义

解释:
- 函数被定义为Jm:Mfc×RKc×p→R+\mathcal{J}_m: M_{fc} \times R^{K_c \times p} \rightarrow R^{+}Jm:Mfc×RKc×p→R+
- 这意味着函数Jm\mathcal{J}_mJm的两个输入是来自两个空间的元素:一个是MfcM_{fc}Mfc空间,另一个是RKc×pR^{K_c \times p}RKc×p空间(这里的RRR表示实数集),而函数的输出是一个正实数R+R^{+}R+
- 函数Jm\mathcal{J}_mJm的表达式为: Jm(U,V)=∑k=1K∑i=1Kcuiksik\mathcal{J}_m(\mathbf{U}, \mathbf{V}) = \sum_{k = 1}^{K} \sum_{i = 1}^{K_c} u_{ik}s_{ik}Jm(U,V)=∑k=1K∑i=1Kcuiksik
- 这里的U∈MfcU \in M_{fc}U∈Mfc是测量重放记忆F\mathcal{F}F的一个c-partition(c划分).
- V=[v1,v2,…,vKc]T∈RKc×pV = [\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_{K_c}]^T \in R^{K_c \times p}V=[v1,v2,…,vKc]T∈RKc×p表示聚类中心的集合。这里vi\mathbf{v}_{i}vi表示第iii个聚类中心,总共有KcK_cKc个聚类中心,每个聚类中心是一个ppp维向量。
- uiku_{ik}uik是fk\mathbf{f}_kfk的隶属函数。如果uik=1u_{ik}=1uik=1,则表示测量数据fk\mathbf{f}_kfk属于第iii个子集(聚类)vi\mathbf{v}_{i}vi;如果uik=0u_{ik}=0uik=0,则不属于。
- siks_{ik}sik表示聚类中心iii与样本kkk之间的相似度,通常用欧几里得距离(Euclidean distance)来度量。sik=∥vi−fk∥22s_{ik} = \|\mathbf{v}_i - \mathbf{f}_k\|_2^2sik=∥vi−fk∥22
然而,在室内定位中,由于环境变化和设备多样性,信号测量不稳定,仅仅利用欧几里得距离来衡量信号测量之间的相似度是不可靠的。
所以本文提出了一个融合相似度模型,考虑到了signal measurements的相对和绝对properties。包含:DIFF distance, HLF distance, and absolute measurement distance。有效的解决设备异构和信号不确定性的问题。(注意:以下的ppp表示基站数。)
- DIFF distance:信号强度差值。

- HLF distance: 信号强度比值。

- Absolute Measurement Distance:欧氏距离。
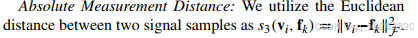
提出了一个融合相似性模型,目的是衡量聚类中心iii和测量样本kkk之间的相似性:
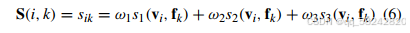
这里的w1、w2、w3w_1、w_2、w_3w1、w2、w3是相应的权重。满足∑l=13exp(−ωl)=1\sum_{l = 1}^{3} \exp(-\omega_l)=1∑l=13exp(−ωl)=1。S\mathbf{S}S是输入数据库F\mathcal{F}F的距离矩阵。
结合式(3)和式(6),可以得到:
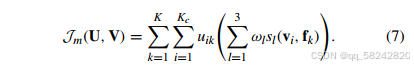
为了增大簇间距离同时减小簇内距离,需要最小化融合权重约束的Jm\mathcal{J}_mJm:
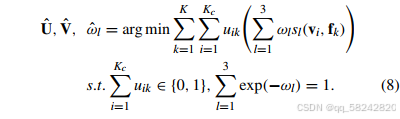
使用拉格朗是乘数法将有约束的优化问题转化为无约束的优化问题(把λ1(∑l=13exp(−ωl)−1)\lambda_1(\sum_{l = 1}^{3} \exp(-\omega_l)-1)λ1(∑l=13exp(−ωl)−1)加进去)因为优化后最优值的时候∑l=13exp(−ωl)\sum_{l = 1}^{3} \exp(-\omega_l)∑l=13exp(−ωl)一定等于1,只有其等于1的时候才会取得最小值。
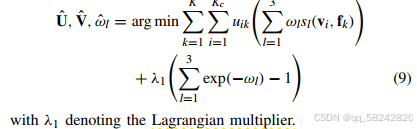
接下来使用coordinate descent坐标下降优化方法进行迭代求最优值,具体分为以下三个步骤:

解释:


其实就是对属于某一簇的所有数据点进行加权平均得到簇的中心点viv_ivi

这里不知道具体怎么求导的????
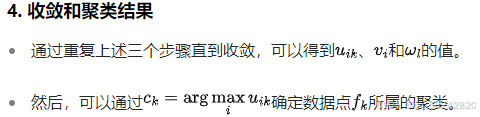
此所提的FuCM中的距离度量sis_isi融合了不同的信号特征,包括RSS、DIFF、HLF。然后得到优化函数式(8),目的是最小化J,利用拉格朗是乘数法将有约束的优化问题转化为无约束的优化问题即式(9),然后利用坐标下降法优化求解uik、vi、wlu_{ik}、v_i、w_luik、vi、wl。这样就实现了簇的分类。并可以根绝uiku_{ik}uik知道measurement fk\mathbf{f}_kfk属于哪个簇。
B. CMDS Space Mapping
CMDS目的:将cluster space转换为positioning space
前面已经使用FuCM将crowdsourcing signal measurements转换为了clusters序列。可以观察到相邻的clusters在真实位置空间中很大可能连接。举个例子,假设聚类5的一个用户可以通过一步step直接移动到距离4或者聚类2,这表明在欧式位置空间上x5\mathbf{x}_5x5的位置与x4\mathbf{x}_4x4和x2\mathbf{x}_2x2的位置很近。(其中xi\mathbf{x}_ixi表示聚类中心vi\mathbf{v}_ivi对应的位置)。所以可以连接每个cluster序列的相邻cluster就可以得到一个cluster拓扑图(a cluster topology)。
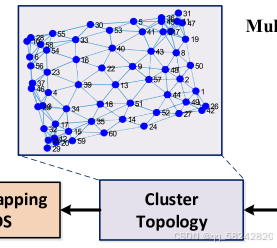
下面可以定义一个聚类中心vi\mathbf{v}_ivi与聚类中心vj\mathbf{v}_jvj之间的连接状态the connection status:(其中Ci,j表示在所有轨迹样本中,从聚类i到聚类j的总的转换次数,我的理解是从轨迹的连续性方面确保聚类的位置是相邻的,满足多次才这两个聚类才可以建立连接C_{i,j}表示在所有轨迹样本中,从聚类i到聚类j的总的转换次数,我的理解是从轨迹的连续性方面确保聚类的位置是相邻的,满足多次才这两个聚类才可以建立连接Ci,j表示在所有轨迹样本中,从聚类i到聚类j的总的转换次数,我的理解是从轨迹的连续性方面确保聚类的位置是相邻的,满足多次才这两个聚类才可以建立连接)
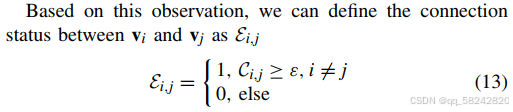

注释:其实εi,j\varepsilon_{i,j}εi,j就是表示两个聚类之间是否连接,如果等于1,说明连接;如果等于0,说明不连接。
接下使用图理论中的最短距离概念,通过以下迭代算法计算所有聚类中心的距离矩阵,用来描述不同聚类之间的距离。
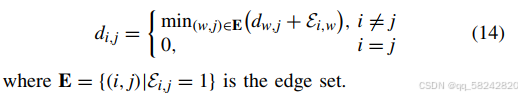

这里ξi,w=0的时候表明聚类\xi_{i,w}=0的时候表明聚类ξi,w=0的时候表明聚类i与聚类与聚类与聚类j之间没有链接,为什么此时还有距离这个概念,此时的距离表示什么????之间没有链接,为什么此时还有距离这个概念,此时的距离表示什么????之间没有链接,为什么此时还有距离这个概念,此时的距离表示什么????
回答:当i=w的时候,ξi,w=0\xi_{i,w}=0ξi,w=0,则距离d就表示的是i到w的距离
假设在位置空间中cluster 中心的对应位置为X=[x1,x2,…,xKc]T\mathbf{X} = [\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_{K_c}]^TX=[x1,x2,…,xKc]T。为了保持空间映射后簇中心之间的几何关系,那么如果di,jd_{i,j}di,j越小,就让xi与xj\mathbf{x}_i与\mathbf{x}_jxi与xj之间的Euclidean distance越近。因此,制定了以下的目标函数:

其中K\mathcal{K}K是与clusters密度相关的尺度参数。由于K\mathcal{K}K的值不会影响cluster centers的相对拓扑,所以这里本文设置K=1\mathcal{K}=1K=1。通过对该目标函数进行优化(我的理解:距离距离d越小,那么聚类的实际位置坐标就越小,所以优化函数L,使其最小,那么|xi-xj|就会近似于dij差不多,也就得到了所谓的相对坐标),可以得到反映clusters中心在positioning space中相对布局relative layout的坐标矩阵X\mathbf{X}X。
另外,利用以下规律推到出绝对布局absolute layout:环境和运动因素通常会导致RSSI测量值的衰减而不是放大。因此,较强的RSSI测量值可以表明用户与相应基站之间的距离较短,一般称为近场条件。
基于此条件,我们可以将mapped position information 与 基站positions关联,得到如下目标函数:

pk\mathbf{p}_{k}pk表示第kkk个基站的位置,qqq是阈值参数。 Xˉ=ΨX+b⊗I=[xˉ1,xˉ2,…,xˉKc]T\bar{\mathbf{X}} = \mathbf{\Psi}\mathbf{X} + \mathbf{b} \otimes \mathbf{I} = [\bar{\mathbf{x}}_{1}, \bar{\mathbf{x}}_{2}, \ldots, \bar{\mathbf{x}}_{K_{c}}]^{T}Xˉ=ΨX+b⊗I=[xˉ1,xˉ2,…,xˉKc]T表示经过线性变换后的坐标矩阵。Ψ∈R2×2\mathbf{\Psi} \in \mathbb{R}^{2\times2}Ψ∈R2×2表示转换矩阵(大小为2×22\times22×2,其实可以理解为对原始的坐标xy进行了一个缩放)。b∈R2\mathbf{b} \in \mathbb{R}^{2}b∈R2(大小为2)表示偏差向量, I∈RKc\mathbf{I} \in \mathbb{R}^{K_{c}}I∈RKc(大小为clusters的数量KcK_{c}Kc)表示元素全为1的向量,其实可以理解为对clusters中心的位置xy进行一个整体的偏移。⊗\otimes⊗ 表示the Kronecker product。另外,为了缓解奇异值问题,qqq应该好好选择,要使得vi\mathbf{v}_ivi中最多只包含一个大于qqq的元素(我的理解是vi\mathbf{v}_ivi表示cluster的中心,他是一个1×p1\times p1×p的向量,其中p的值表示基站数,向量的值表示每个基站的RSSI,相当于只能有其中一个基站的RSSI大于设定的阈值qqq,相当于确保只有信号最强的那个基站的位置距离cluster中心的位置最近。)
引:Kronecker product

通过最小化式(15)和式(16)中的目标函数,我们可以确定所有聚类中心的映射位置。因此,我们可以使用基于聚类中心位置的加权分类方法进行定位任务。
C. Optimization
1. 求解相对位置坐标X{\mathbf{X}}X

2. 求解绝对位置坐标Xˉ=ΨX+b⊗I\bar{\mathbf{X}} = \mathbf{\Psi}\mathbf{X} + \mathbf{b} \otimes \mathbf{I}Xˉ=ΨX+b⊗I

需要至少已知位置的基站。
D. Online Updates and Positioning
为了使定位模型适应环境的变化,本文使用了以下的方法(个人感觉没啥创新点)
首先,F\mathcal{F}F记录第一次收集的K\mathbf{K}K个信号测量值。随后,新收集的测量值也堆到F\mathcal{F}F里面,然后将相同数量最旧的测量值从 F\mathcal{F}F中删除掉。这样处理以后,基于新的F\mathcal{F}F重新使用所提的ENAP方法计算出一个新的定位模型。
如何定位:
使用cluster centers vi\mathbf{v}_ivi和其对应的位置坐标xˉi\bar{\mathbf{x}}_ixˉi,训练一个K-nearest neighbor (KNN) classifier,用KNN建立一个从cluster space到positioning space的桥梁。
给定一个testing measurement sample fk\mathbf{f}_kfk,首先使用式(6)计算它与cluster centers的距离
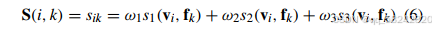
然后,通过选择最近的K个cluster centers,计算相应的位置坐标均值,从而可以推导出这个样本的位置。

具体的算法流程如图所示:

5. Experimental results
A. Simulation Experiments
1)Environmental settings:
20x20米的房间,部署9个基站,在室内随机走动,记录每个轨迹点的信号测量值。用户的方向随机选择:前、后、左、右、左前、左后、右前、右后、静止(9个方向)
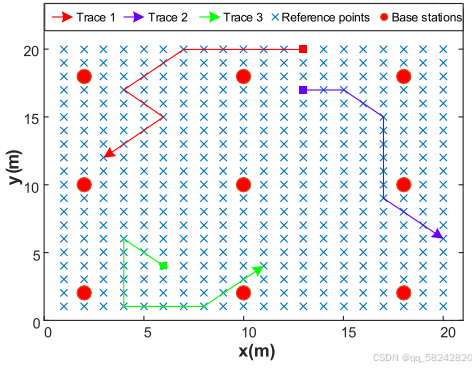
对于每个用户,通过使用一下路径损失对数正态阴影模型(path loss log-normal
shadowing model???)沿着移动轨迹生成RSS测量值:
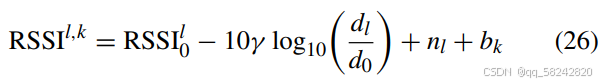

注释:根据用户与基站的距离生成RSSI值,同时考虑了SNR引起的噪声和设备异构性引起的误差,另外还考虑了基站不能被检测到的情况。


2)Comparison Algorithms:
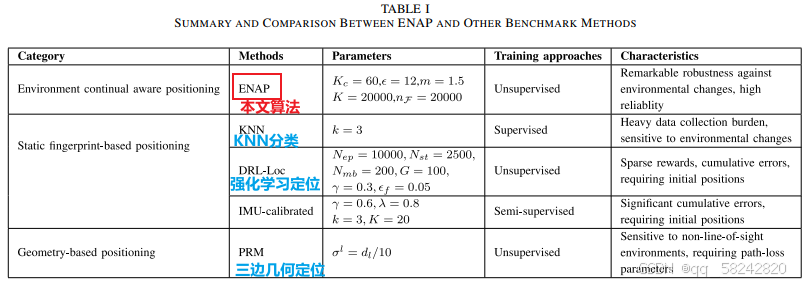
使用average positioning results来评估定位精度。

3)Positioning Performance
Short-Term Positioning Accuracy:
Space mapping results:利用无监督众包数据,通过ENAP算法推出cluster layouts(在未知floor plan information先验信息情况下)
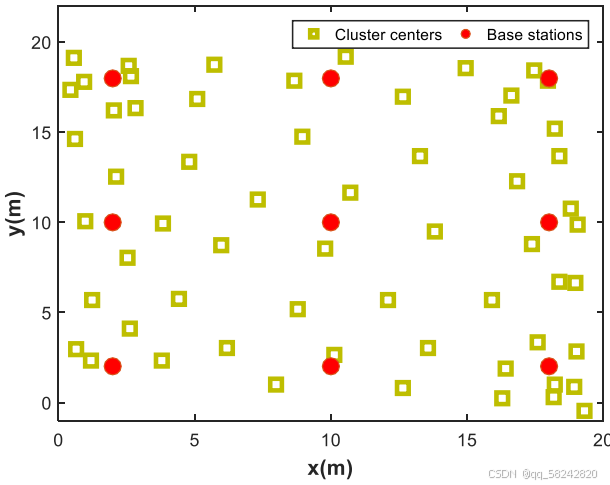
定位结果:
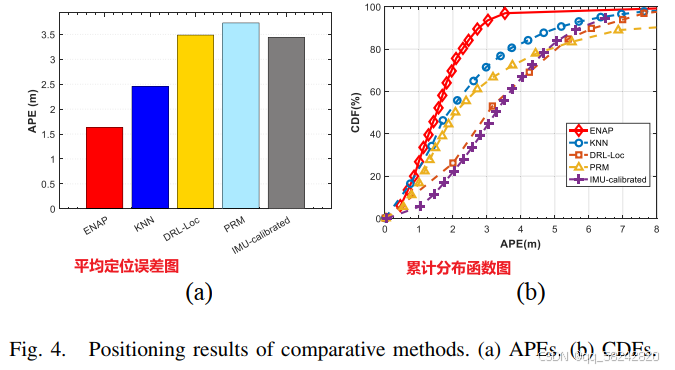
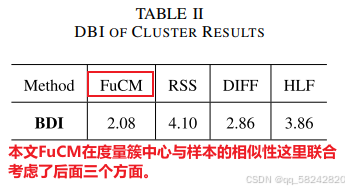
Cluster Performance:
采用Davies–Bouldin index (DBI) 评价网络的聚类效果(通过度量簇内相似度与簇间不相似度),DBI越小说明聚类效果越好,DBI定义如下:

聚类结果:
Comparison of Continual Environmental Awareness:
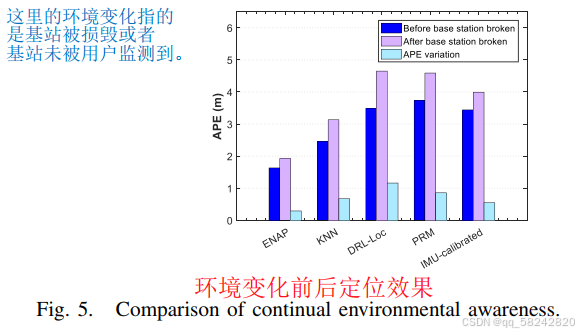
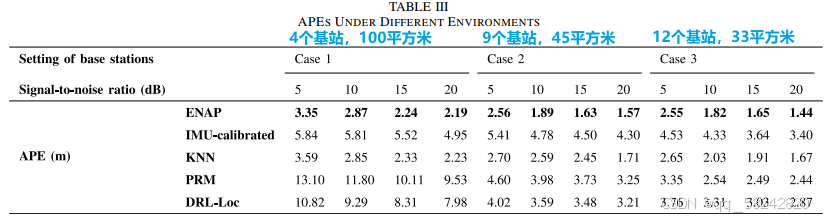
Parameter Analysis:
考虑基站部署(每个基站的覆盖范围不同)与信噪比对定位精度的影响:
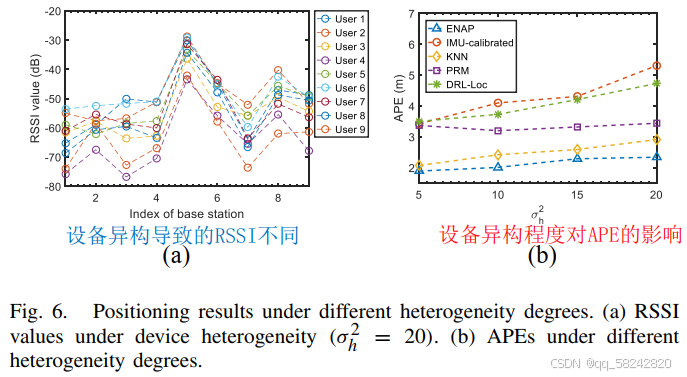
设备异构性对定位精度的影响:






















 1938
1938

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








