计算机视觉——相机标定

目录

一.相机标定

二.相机标定要标定什么？

 三.算法原理

3.1. 算法步骤

3.2 方程和约束条件

 b是要求解相机内参的未知量， B是通过b构造的对称矩阵

 3.3 极大似然估计

四.opencv代码实现

实验数据

实验结果

---

一.相机标定

相机标定指建立相机图像像素位置与场景点位置之间的关系，根据相机成像模型，由特征点在图像中坐标与世界坐标的对应关系，求解相机模型的参数。相机需要标定的模型参数包括内部参数和外部参数。

针孔相机成像原理其实就是利用投影将真实的三维世界坐标转换到二维的相机坐标上去，针孔相机模型如下：

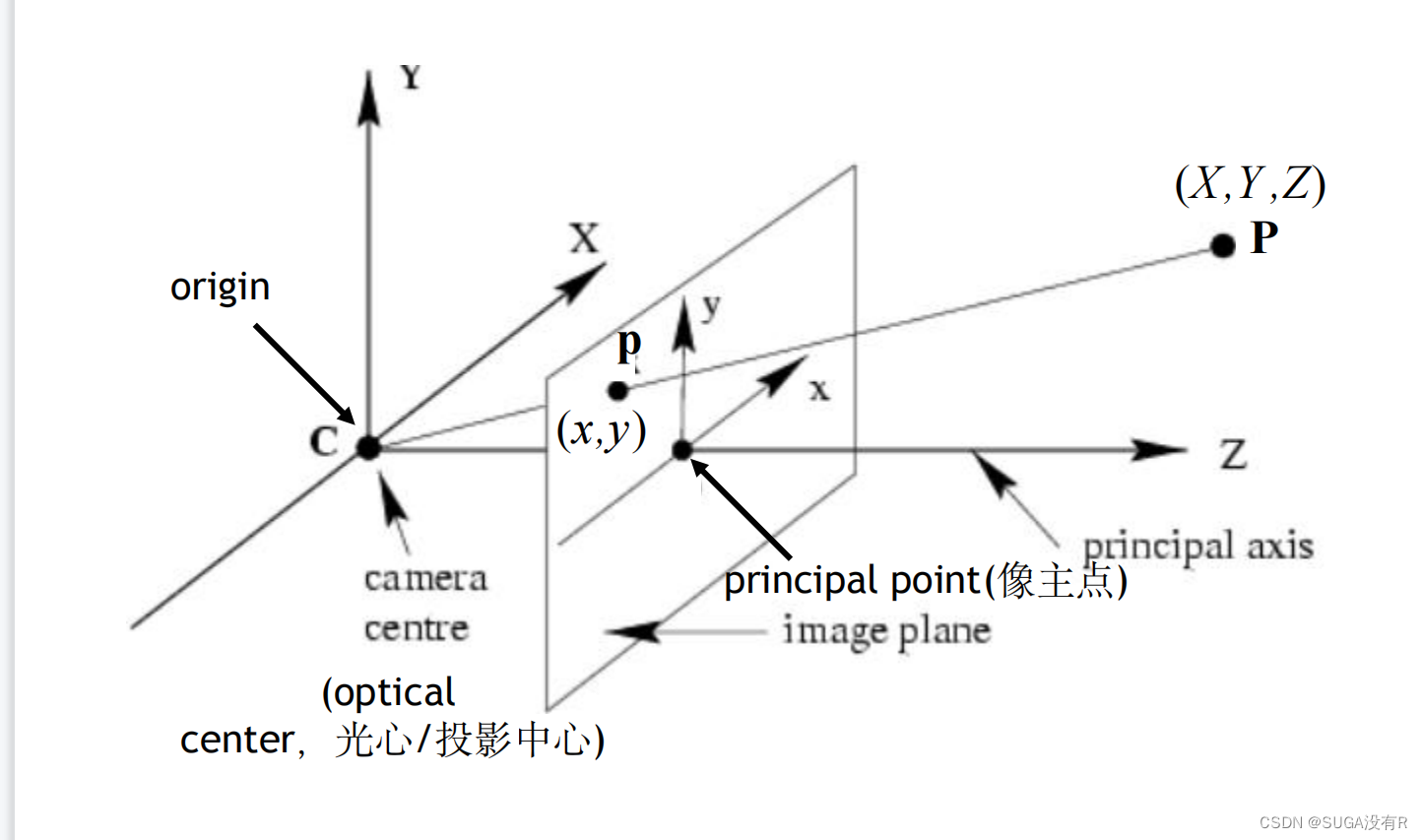
 从图中我们可以看出，在世界坐标中的一条直线上的点在相机上只呈现出了一个点，其中发生了非常大的变化，同时也损失和很多重要的信息，这正是我们3D重建、目标检测与识别领域的重点和难点。实际中，镜头并非理想的透视成像，带有不同程度的畸变。理论上镜头的畸变包括径向畸变和切向畸变，切向畸变影响较小，通常只考虑径向畸变。
 

图像径向畸变原因：

（1）透镜质量原因

（2）光线在远离透镜中心的地方比靠近中心的地方更加弯曲

用数学公式表达：

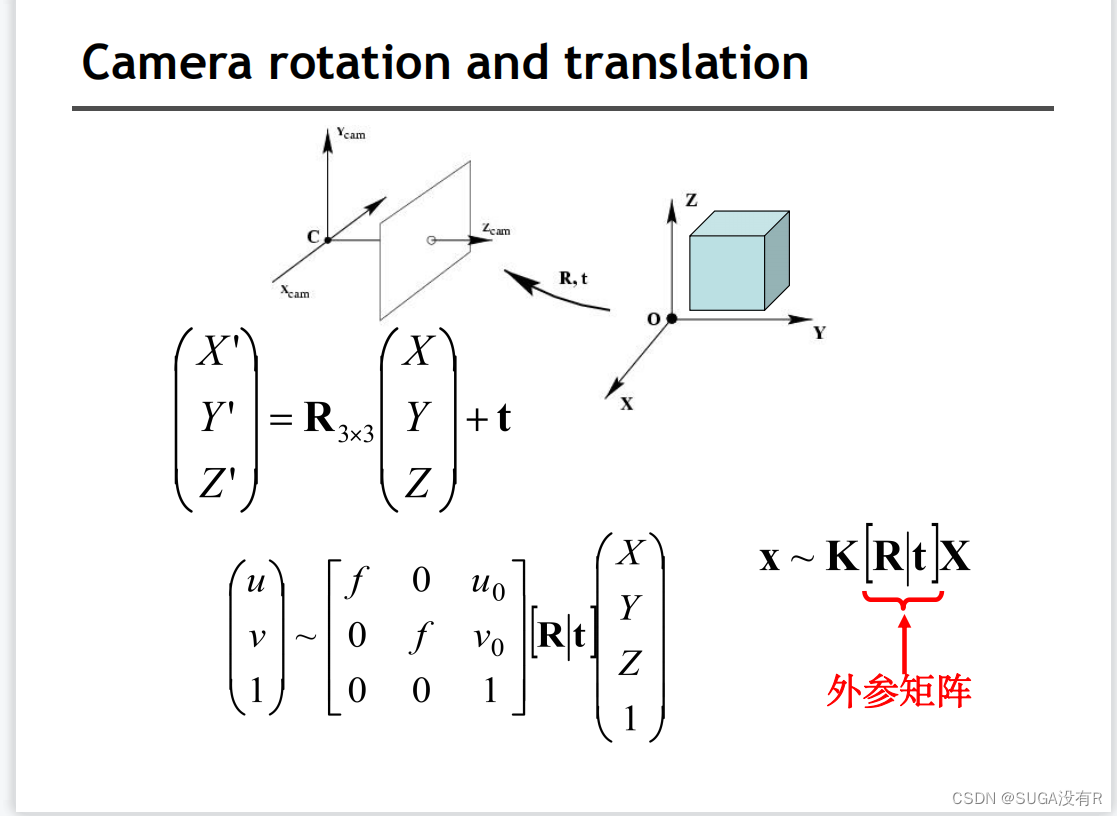
其中K为内参矩阵，是相机内部参数组成的一个3*3的矩阵

二.相机标定要标定什么？

• 相机内部参数/内方位元素：焦距(f，唯一未知量)、像主点坐标（u,v是光线坐标轴和图像平面的交点）、畸变参数(s)
• 相机外部参数/外方位元素：旋转矩阵（R）、平移矩阵描述照相机中心位置的三维平移向量（t)

纵横比例参数a是在像素元素非正方形的情况下使用的。通常情况下可以默认为1。

 三.算法原理

3.1. 算法步骤

1.  打印一张棋盘格A4纸张&#x