目录
一.Logicstic回归的一般过程
(1)收集数据;(2)准备数据;(3)分析数据;(4)训练算法;(5)测试算法;(6)使用算法;
Logicstic回归分类主要思想:根据现有数据对分类边界线建立回归公式,以此分类。
这里的“回归”表示要找到最佳拟合参数集,训练分类器时的做法就是寻找最佳拟合参数,使用的是最优化算法。
1.logicstic:
优点:计算代价不高,易于理解和实现
缺点:容易欠拟合,分类精度可能不高
适用数据类型:数值型和标称型数据
2.sigmoid函数
Sigmoid函数是一种阶跃函数( step function )。在数学中,如果实数域上的某个函数可以用半开区间上的指示函数的有限次线性组合来表示,那么这个函数就是阶跃函数。而数学中指示函数(indicator function)是定义在某集合X上的函数,表示其中有哪些元素属于某一子集A。
具体计算公式为:
为了实现Logistic回归分类器,我们在每个特征上都乘以一个回归系数,然后把所有的结果值相加,将这个总和代人Sigmoid函数中,进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类,小于0.5即被归入0类。所以,Logistic回归也可以被看成是一种概率估计。
2.1:Logicstic回归:分类问题

对数线性回归是 g(∙)=ln(∙) 时广义/多维线性模型的特例。𝑙ny= wx + b
Sigmoid函数的输出记为z,公式为:

运用Sigmoid函数:

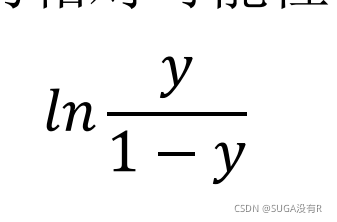








 本文深入探讨了Logistic回归,包括其分类原理、sigmoid函数、极大似然法以及通过梯度上升法优化回归系数的过程。通过实例展示了如何使用Logistic回归预测病马的死亡率,并对比了梯度上升法与随机梯度上升法的优缺点。
本文深入探讨了Logistic回归,包括其分类原理、sigmoid函数、极大似然法以及通过梯度上升法优化回归系数的过程。通过实例展示了如何使用Logistic回归预测病马的死亡率,并对比了梯度上升法与随机梯度上升法的优缺点。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








