算法笔记三之表格法解Dijkstra算法（贪心算法）【应试版】

提示：本文章不含代码，纯应试解题~（中国地质大学（武汉）研究生算法考试题目）

---

前言

Dijkstra算法是一种用于在图中找到从单个源点到所有其他顶点的最短路径的算法。它由荷兰计算机科学家艾兹格·戴克斯特拉（Edsger W. Dijkstra）在1956年提出。这个算法属于贪心算法的一种，因为它在每一步都做出局部最优的选择，即选择当前已知的最短路径，希望这样能导致全局最优解。

---

一、Dijkstra算法

Dijkstra算法的核心思想是维护一个未访问顶点集合，这个集合中的每个顶点都有一个与源点的距离估计值。算法从源点开始，初始化源点到自身的距离为0，到其他所有顶点的距离为无穷大。然后，算法不断选择未访问顶点中距离最小的顶点，更新其相邻顶点的距离，并将该顶点标记为已访问。这个过程一直进行，直到所有的顶点都被访问过。

说人话就是—— 想象一下，你在一个陌生的城市里，手里有一张地图，你想从你现在的位置（我们叫它源点）出发，找到去其他所有地方的最短路线。Dijkstra算法就像是一个智能的导航系统，帮你找到这些最短路线。

二、问题描述

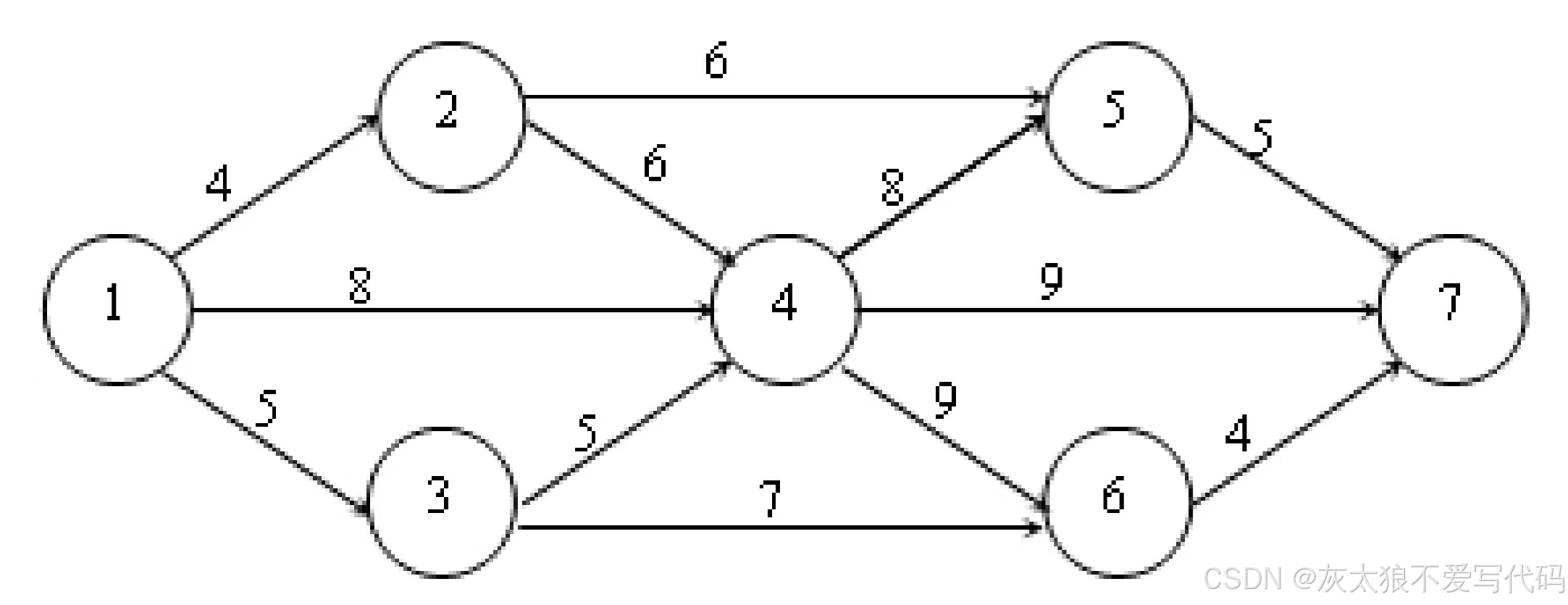
用贪心算法（Dijkstra算法）求下面网络中从结点1出发到其余各个结点的最短路径。（要求给出中间过程，只给出最后结果没有中间过程不得分）

三、表格法解题

核心： Dijkstra算法本质上是贪心算法，每次都要选中离结点1最近的结点，然后更新（最关键的一句话，请记住~）

所谓表格法，首先肯定是要画一个表格啦~这里就会涉及到几行几列的问题——对于列来说，图中除了结点1外还有几个结点，那么就有几列（名称写第*次）；对于行来说，列数保持一致（名称写结点编号）。不过最后一行还要加一行（名称叫终点集），这表示结点1到距离它最短的结点的路径。如下表所示：

	第一次	第二次	第三次	第四次	第五次	第六次
结点2
结点3
结点4
结点5
结点6
结点7
终点集	{}	{}	{}	{}	{}	{}

• 接下来我们会在这张表上进行解题，为了便于演示，每一步都会画一次这个表，并且保存之前的内容。当然，考试的时候，画一张表就足够啦~

温馨提示：除了结点1外，还有几个结点就会有几步哦，而且我们一步只处理一列

第一步