损失函数笔记

1.回归问题损失函数

1.1 均方误差损失函数

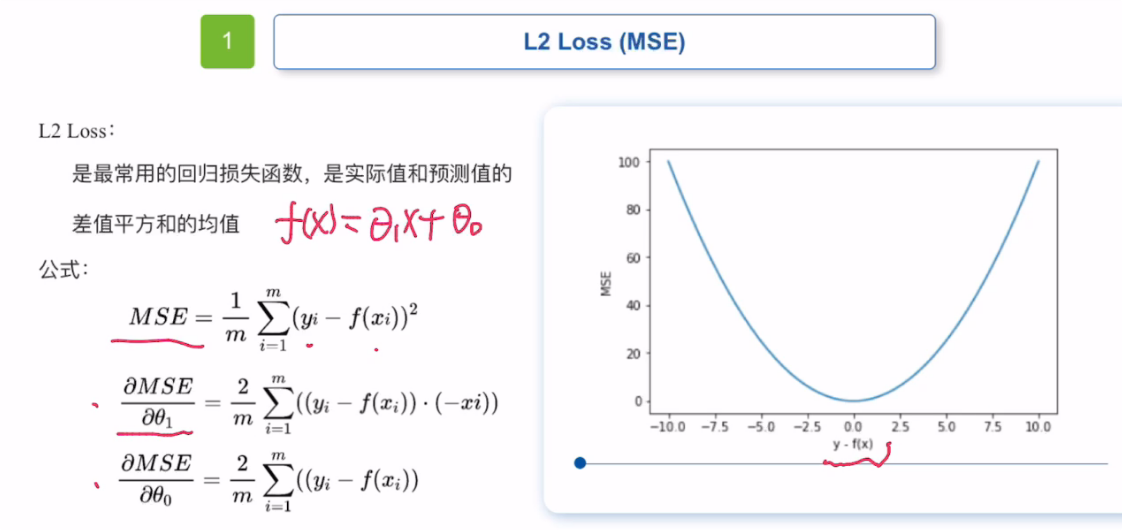
均方误差损失函数也称MSE损失函数。

经常用于解决一些回归问题。是最常见的损失函数，

MES损失函数是实际值和预测值的差值平方和的均差。

MSE损失函数即使学习率固定，也会收敛，当损失值趋近于0时会逐渐降低，从而让它的模型在训练收尾时更准确。

2.2 平均绝对误差损失函数

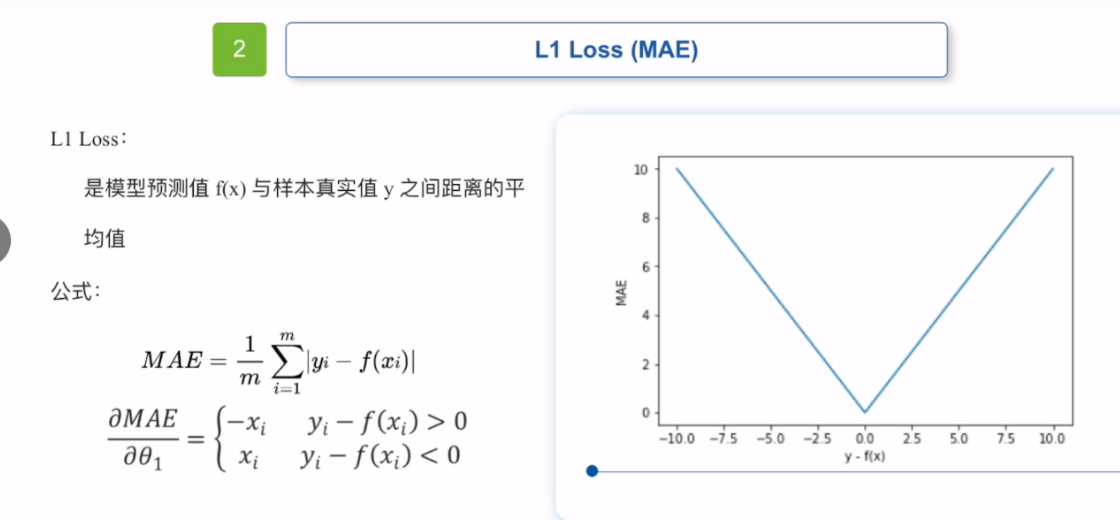
平均绝对误差损失函数就是MAE损失函数

MAE损失函数梯度始终一样，即使很小的损失，梯度也很大，很难收敛到更高的精度，（建议和动态学习率一起使用。）

经常用于解决一些回归问题。是最常见的损失函数，

Mas损失函数瑟吉欧，模型预测值f(x)和样本真实值y之间距离的平均值。

总体来说，MAE会对误差较大的数据给与较大的惩罚，对误差较小的数据给与更小的惩罚。

MAE对离群值没有特别敏感，和MSE相比 离群值对MAE的影响较小。

3.3 Huber Loss损失函数

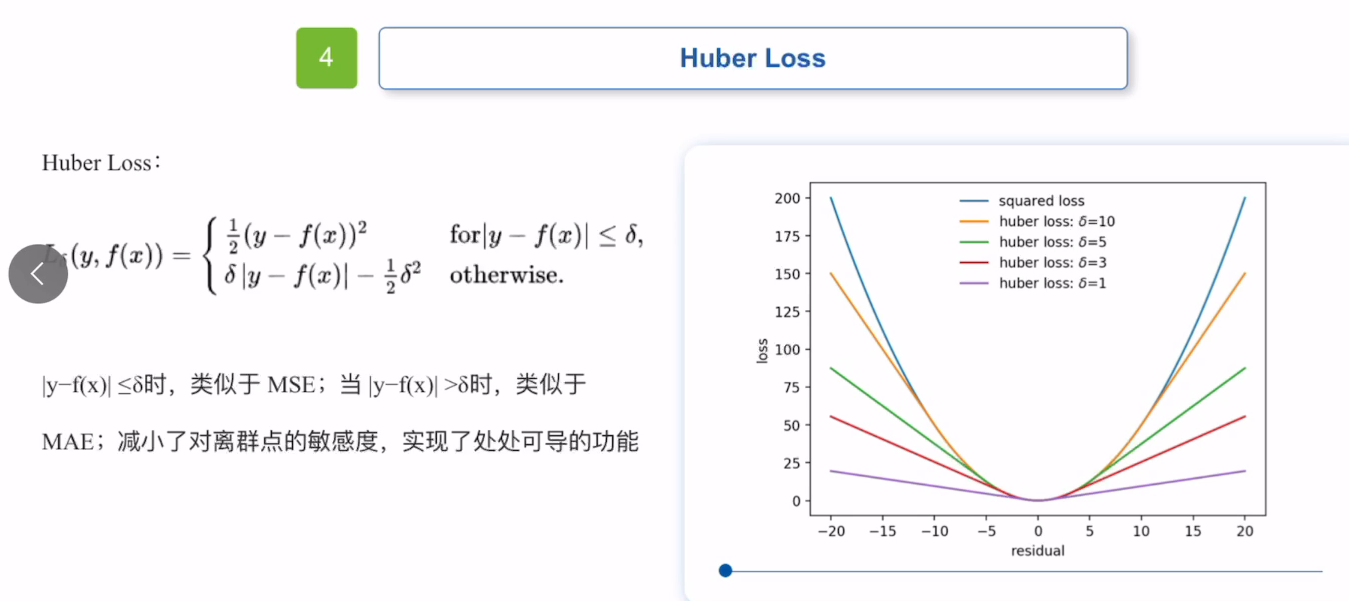
huber loss损失函数综合了MAS和MES的优点，引入了一个超参数derta，derta的引入让Huber Loss函数。当超参数取不同值时，它的函数不同。

他通过设定的derta来衡量离群值的敏感度，并根据derta来调整自己的策略。

2. 分类问题损失函数

2.1 交叉熵损失函数

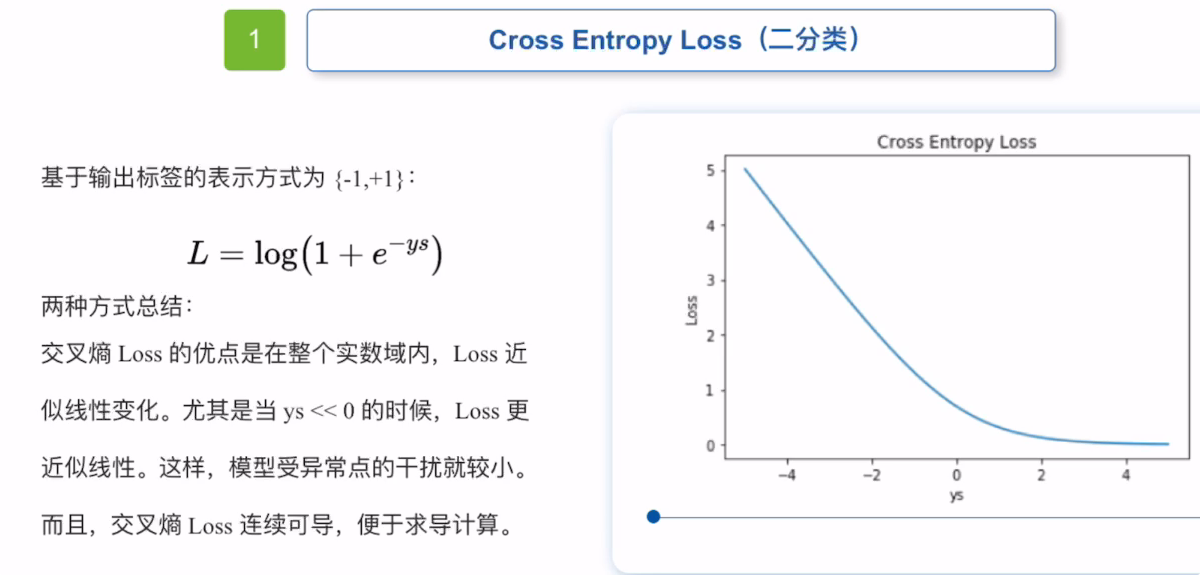
熵可以衡量一个随机变量的不确定性，在处理二分类问题时，最常用的损失函数为交叉熵损失函数。

交叉熵损失函数主要用于处理二分类问题。

它的输出标签表示为【0,1】，首先loss近似线性变换，模型受异常点的干扰较小，并且交叉熵损失函数连续可导，可以进行求导计算。

2.2 合页损失函数

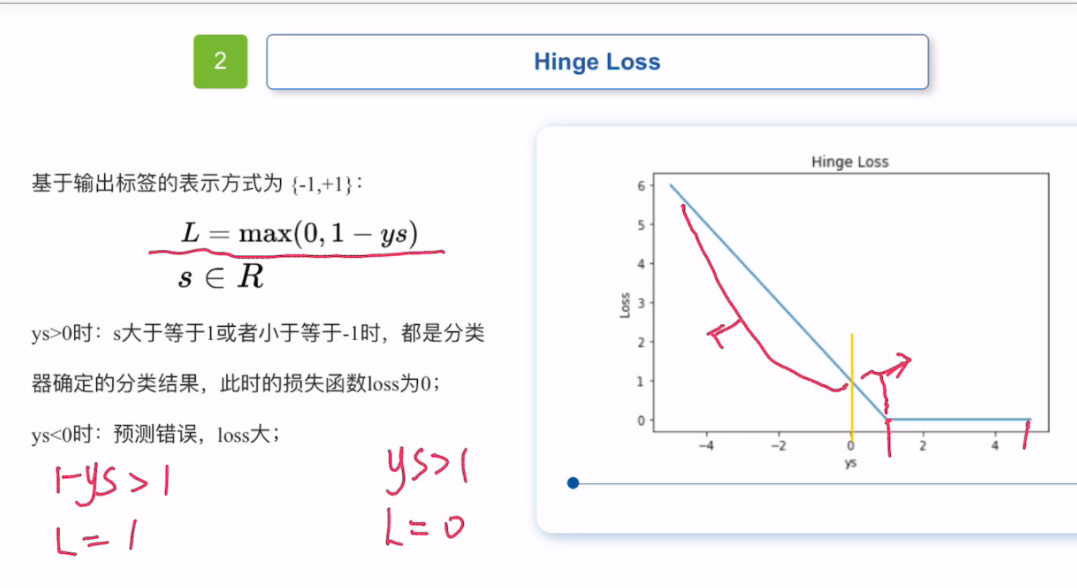
hinge loss” 中文名叫 “合页损失函数” 或 “折页损失函数”。

它主要用于支持向量机（SVM）等机器学习算法中的最大间隔分类任务。

当ys>0时，s≥1或者≤-1都是分类器确定的结果，此时损失函数loss为0，

当ys<0时，预测错误，loss大

2.3 指数损失函数

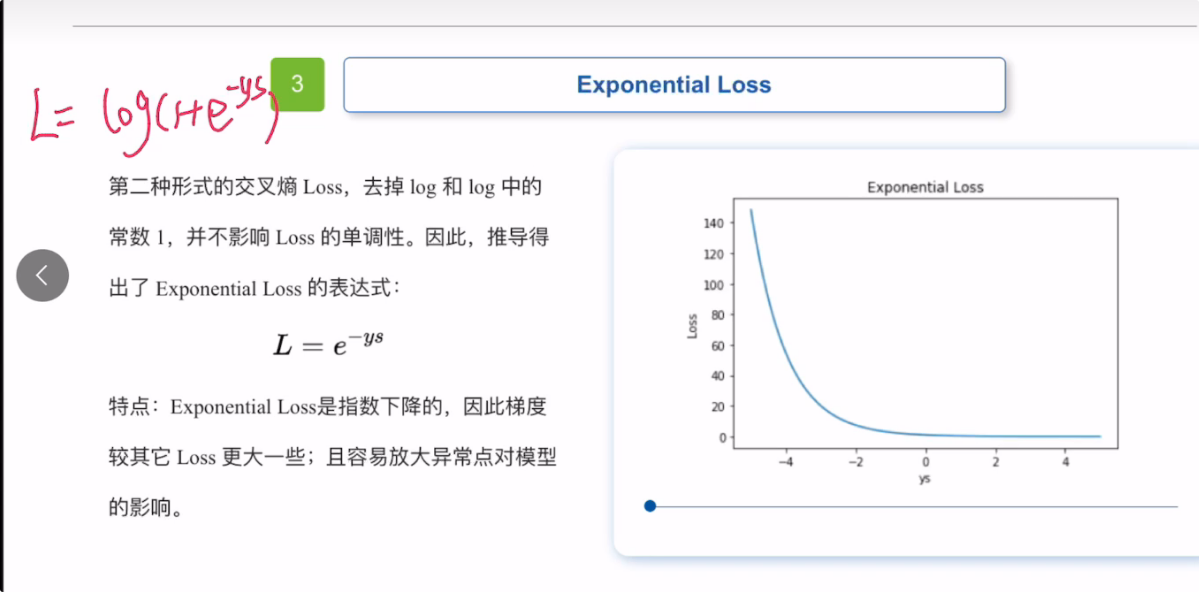
这是第二种形式的交叉熵损失函数，他去掉了log和log中的常数1，并且不影响损失函数的单调性。

指数损失函数，是指数下降的，他的梯度相比其他loss更大一些，更容易放大异常点对模型的影响。

和MAE一样对异常点敏感

2.3 多类别损失函数

信息量：衡量信息量的大小就是看这个信息消除不确定性的程度，信息量的大小与信息发生的概率成反比，信息发生概率越高，信息量越低，信息发生概率月底，信息量越高。

信息熵：可以表示对所有信息量的期望，期望是实验中每次可能结果的成绩和可能结果的概率以及其结果的总和。

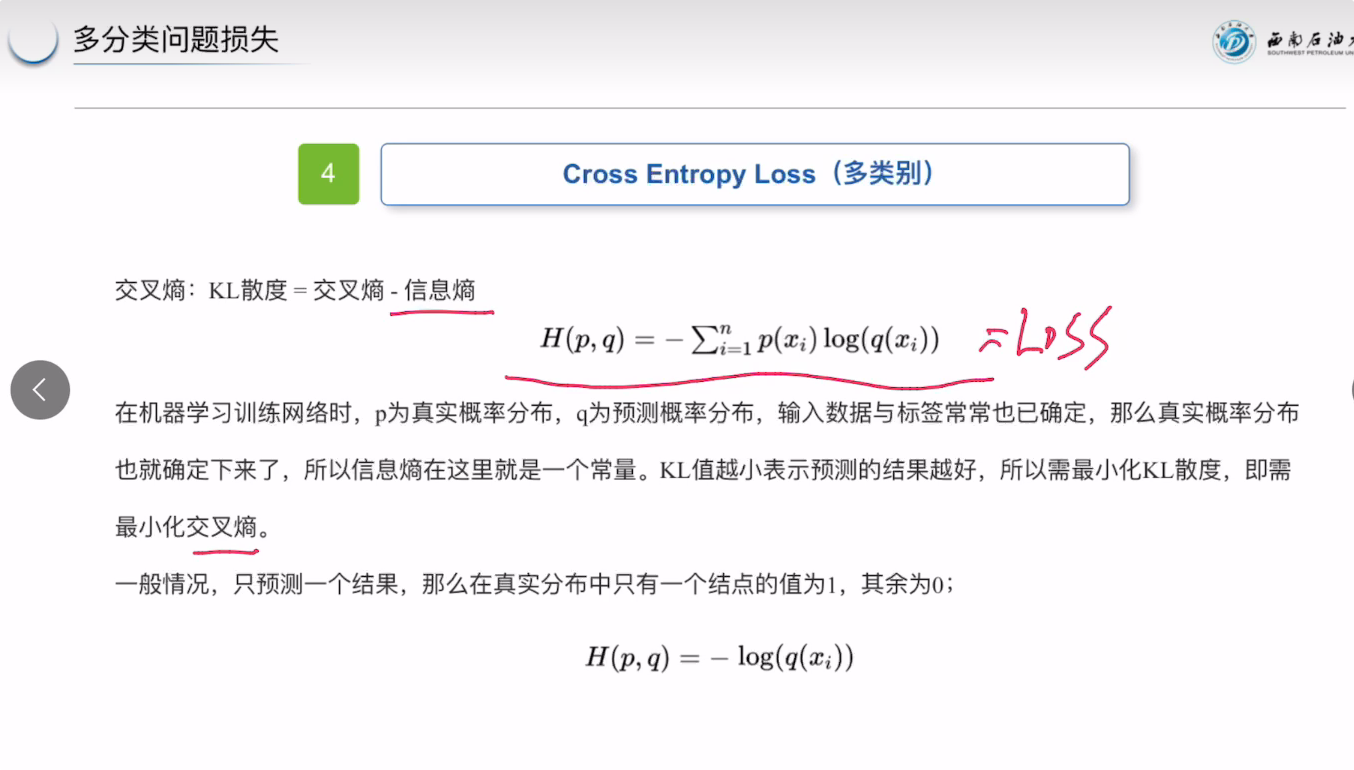
交叉熵（KL散度）：衡量这两个概率分布之间的差异，KL散度越小，交叉熵和信息熵也就越接近。

交叉熵也就是KL散度。

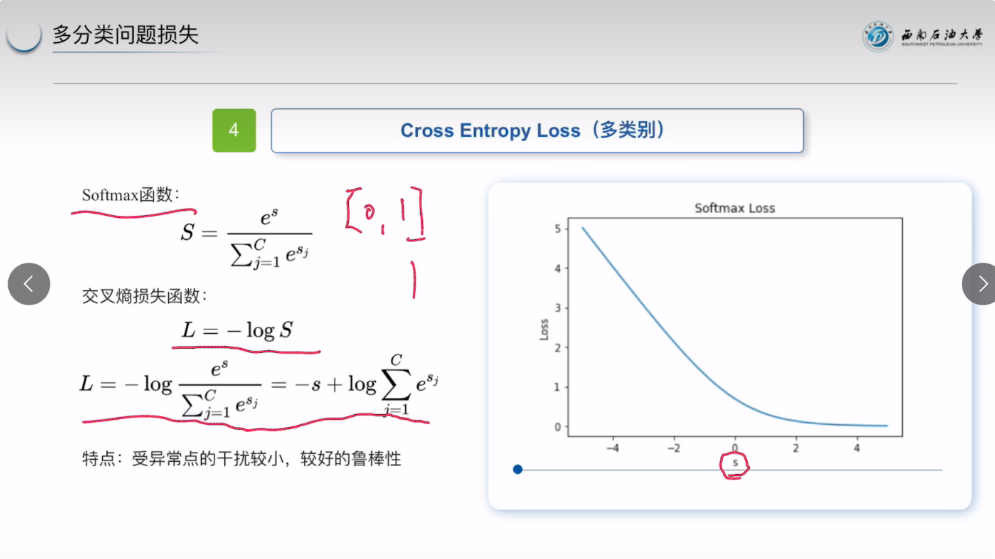
类别损失函数最大的优点就是受异常点干扰小，有较强的鲁棒性。