代码随想录刷题攻略---数组3--滑动窗口/前缀和

La fire

已于 2024-11-10 23:41:52 修改

阅读量104

点赞数

分类专栏：代码随想录刷题文章标签：数据结构 c++ c语言算法

于 2023-10-27 23:41:34 首次发布

本文链接：https://blog.youkuaiyun.com/qq_54990658/article/details/134083945

版权

代码随想录刷题专栏收录该内容

21 篇文章

订阅专栏

题例：

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

此题的暴力解法是双层遍历，即O(n^2)的时间复杂度。这里提出一种O(n)的方法，即滑动窗口。

滑动窗口

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环完成了一个不断搜索区间的过程。

那么滑动窗口如何用一个for循环来完成这个操作呢。

首先要思考如果用一个for循环，那么应该表示滑动窗口的起始位置，还是终止位置。

窗口就是满足其和 ≥ s 的长度最小的连续子数组。

窗口的起始位置如何移动：如果当前窗口的值大于等于s了，窗口就要向前移动了（也就是该缩小了）。

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

解题的关键在于窗口的起始位置如何移动，如图所示：

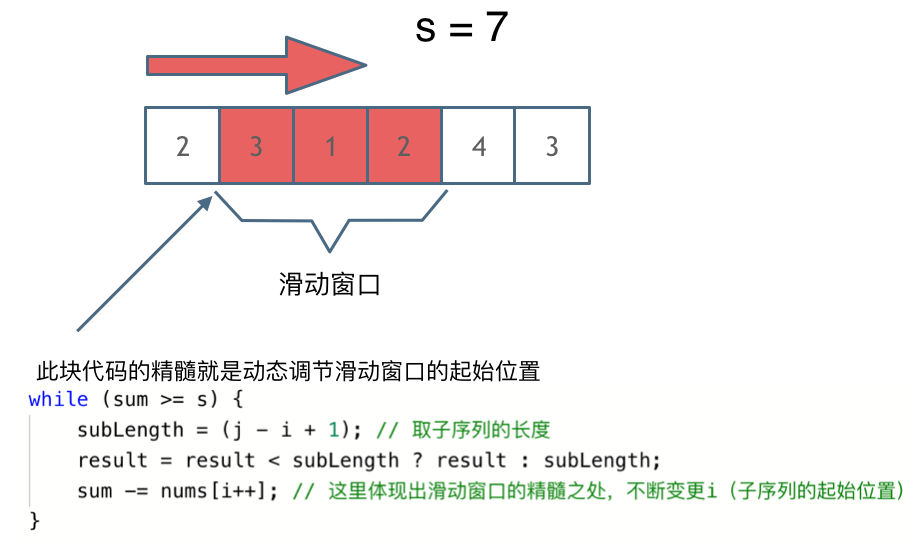
leetcode_209

可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

滑动窗口使用两个移动指针，指针范围内的子数组就是一个窗口；不断调整窗口的大小和位置，使窗口内的子数组符合我们的要求，就是滑动窗口的使用目的。

在此题中，我们的窗口初始大小为 1 ，窗口的左边界和右边界都指向nums[0]。此时窗口内的总值sum = nums[0]，在总值没有达到target之前，我们不断地将有窗口向右移动，更新sum。若某一时刻窗口内的sum == target，那么返回窗口的大小即可。

若窗口内的sum > target，说明此时以左边界起始的窗口不能达到要求，我们将左窗口向右边，即下一个元素移动，更新窗口的左边界（此时要把原本左窗口的值从sum中减去）。

code:

扩展题1：水果成篮

这道题的思路也比较清晰，窗口的右边界向右扩展，记此时水果数量（即窗口的长度）。若此时窗口内的元素种类超过2种，左边界就要向右收缩，知道窗口内的水果种类为2为止，比较两种情况下水果数量谁更多。

这题的难点在于记录窗口内的水果种类，用unordered-map来记录会比较方便（若用数组或者变量来记录会分不清哪个种类先摘哪个后摘）

code:

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int total=INT_MIN;
        int i=0;
        int j=0;
        //int type=1;
        //int temp=0;
        unordered_map<int, int> cnt; //种类->数量，方便遍历时判断这个种类是否已经存在
        for(j;j<fruits.size();++j)
        {
            ++cnt[fruits[j]];//该种类的水果数量++
            while(cnt.size() > 2)//种类满了后，将同种类退出
            {
                // --cnt[fruits[i]];
                // i++;
                //为了指定代表i指向的水果种类，必须用指针来指向这个键值对
                auto it = cnt.find(fruits[i]);//指针指向相应键的键值对
                -- it -> second;
                if(it -> second == 0)
                cnt.erase(it);
                i++;
            }
            total = total > j-i+1 ? total : j-i+1;//权值为1，则窗口长度就是数量
        }
        
        return total;
    }
};

扩展题2：连续子串和的整除问题

问题描述

小M是一个五年级的小学生，今天他学习了整除的知识，想通过一些练习来巩固自己的理解。他写下了一个长度为 n 的正整数序列 a_0, a_1, ..., a_{n-1}，然后想知道有多少个连续子序列的和能够被一个给定的正整数 b 整除。你能帮小M解决这个问题吗？

测试样例

样例1：

输入：n = 3,b = 3,sequence = [1, 2, 3]
输出：3

样例2：

输入：n = 4,b = 5,sequence = [5, 10, 15, 20]
输出：10

样例3：

输入：n = 5,b = 2,sequence = [1, 2, 3, 4, 5]
输出：6

这道题用前缀和+滑动窗口的思想去做。

前缀和的原理如下：

例如，我们要统计 vec[i] 这个数组上的区间和。

我们先做累加，即 p[i] 表示下标 0 到 i 的 vec[i] 累加之和。

如图：

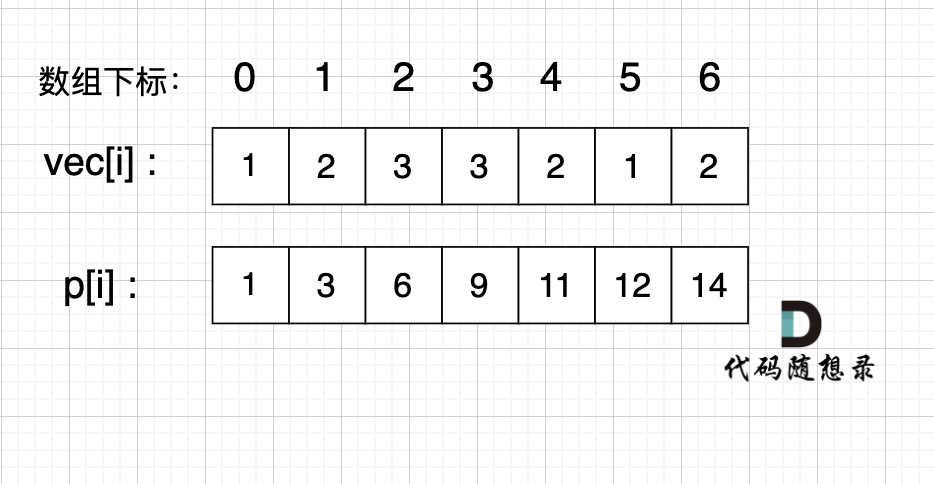
如果，我们想统计，在vec数组上下标 2 到下标 5 之间的累加和，那是不是就用 p[5] - p[1] 就可以了。也就是说前缀和的数组上保存着原数组连续位置的和，所以前缀和适用于求解数组中的连续问题。

该题目正好跟数组的连续问题有关，我们使用一个窗口在前缀和数组中滑动，统计能被整除的连续子数组和就可以求解。

public static int solution(int n, int b, List<Integer> sequence) {
        // 前缀和求解？正整数数列
        if(sequence.size()==1)
        {
            if(sequence.get(0)%b==0)
            return 1;
            else
            return 0;
        }
        int[] prefix=new int[sequence.size()+1];
        int i,j;//左右指针
        int sum=0;
        for(i=0;i<sequence.size();i++)
        {
            prefix[i]=sum;//第一个数是0
            sum+=sequence.get(i);
        }
        prefix[i]=sum;
        i=0;
        //j=i+1;
        int len=0;
        while(i<sequence.size())//3
        {
            for(j=i+1;j<=sequence.size();j++)
            {
                if((prefix[j]-prefix[i])%b==0)
                {
                    len++;
                }
            }
            i++;//往右挪动
        }
        return len;
    }