文章介绍了如何使用深度优先搜索(DFS)解决岛屿问题，包括岛屿的数量、周长、面积等。通过分析DFS和BFS的区别，以及在二叉树和网格结构中的应用，阐述了在网格中应用DFS的基本步骤和注意事项，并提供了相关LeetCode题目的示例。
最近遇到的这个关于岛屿类的场景题，感觉不咋会，所以特地学习了一下，写个博客来记录一下我的学习过程。
做过的佬们可能很快就能AC这道题目，因为这类题有一个通用的解法，那就是深度优先搜索， 对于我这样的小白来说还是很困难的（学过，脑子记住了，过一段时间再看，WC 这是啥？所以记笔记还是很有用的~！）下面就来讲解一下此类问题。
先来几道题目镇个场子~~
1254. 统计封闭岛屿的数目 - 力扣（LeetCode）
前情概要
感觉肿么样老铁们，是不是都不会（doge），开玩笑的，相信你们应该都会。。呃，对吧，嗯一定是的！！！
开篇之前我们先来补习一下关于 深度优先遍历（DFS）和 广度优先遍历（BFS）的一些相关知识。
当处理图或树等数据结构时，深度优先搜索（DFS）和广度优先搜索（BFS）是两种最常用的搜索和遍历算法。
深度优先搜索（DFS）：
1. 从起始节点开始，沿着一条路径尽可能深入地访问节点，直到到达不能继续访问的节点为止。
2. 当访问一个节点时，将其标记为已访问，并继续向下遍历与该节点相邻的尚未访问的节点。
3. 当遍历到一个节点时，会继续沿着它的一条路径直到遇到不能继续访问的节点，然后回退到前一个节点，尝试探索其他路径。
4. 递归是实现DFS算法的常见方式，每次递归调用都相当于深入到更深的层次。广度优先搜索（BFS）：
1. 从起始节点开始，首先访问起始节点，然后访问起始节点的所有相邻节点。
2. 然后访问这些相邻节点的相邻节点，并且以此类推，逐层地向外扩展。
3. 在BFS中，我们使用队列来存储待访问的节点，每次从队列中取出一个节点进行访问，并将它的所有相邻节点加入队列。
4. 通过队列先进先出的特性，我们可以逐层地向外扩展，从而遍历所有与起始节点相连通的节点。DFS和BFS的区别：
1. DFS是一种递归的搜索算法，通过深入到较深的层次，先遍历与起始节点直接相连的节点，再逐步回溯，继续遍历其他未访问的节点。
2. BFS是一种迭代的搜索算法，通过广度优先遍历，先访问与起始节点直接相连的节点，然后逐层地向外扩展，直到遍历完所有与起始节点相连通的节点。DFS和BFS在不同情况下有不同的应用场景:
1. DFS常用于寻找图中路径、拓扑排序、连通性检测等问题。
2. BFS常用于图的最短路径问题、生成连通分量、层次遍历等问题。
总的来说，DFS和BFS都是非常有用且广泛应用于图、树等数据结构的搜索和遍历算法，它们通过不同的搜索策略，在不同的场景中发挥着重要的作用。
细节铺垫
知道了啥是啥，我们来深入题目了解。对于岛屿问题我们所说的 DFS 是一种在 ‘’网格‘’ 结构中进行的一类代表。相比于树的 一入到底 ，网格结构的遍历要比其麻烦很多，没有掌握方法很难理解透彻，自然就不知道咋A。
下面带入场景中，啥是网格模型？结合问题来说，网格问题是由 m×n 个方格组成的一个大网格，每个网格都有上、下、左、右四个方格相邻，靠近边界的可视为一堵墙，但其仍有相邻的小方格，即该网格的四条边均被水包围。每个格子中的数字可能是1或者0,1视为海洋，0视为陆地，那么相邻的陆地就变成了岛屿了。
在这样一个设定下，就出现了各种岛屿问题的变种，包括岛屿的数量、面积、周长、子岛屿等。不过这些问题，基本都可以用 DFS 遍历来解决。
知识拓展
先说一下DFS的基本结构：
DFS的基本结构通常是通过递归实现的，其基本步骤如下：
1. 判断递归的终止条件：在递归的开始部分，判断是否满足递归终止条件。如果满足条件，直接返回或执行其他操作，结束递归过程。
2. 处理当前层逻辑：在递归终止条件之后，处理当前层的逻辑。这包括对当前层进行一些操作，比如访问当前节点、记录信息等。
3. 进入下一层递归：在当前层逻辑处理完毕后，根据问题的具体情况，进入下一层递归。这可能包括向下一个节点递归、向相邻节点递归等。
4. 恢复状态（可选）：在从下一层递归返回到当前层时，可能需要恢复状态。这是因为递归函数的执行会修改一些全局或共享的变量，为了避免影响其他递归路径，需要在返回时恢复状态。
基本结构的伪代码如下：
void dfs(参数) { // 递归终止条件 if (满足终止条件) { return; } // 处理当前层逻辑 进行一些操作，比如访问当前节点、记录信息等 // 进入下一层递归 dfs(下一层递归参数); // 恢复状态（可选） 恢复一些状态，将当前层递归执行的影响消除 }在DFS算法中，递归的核心是不断地向下递归，直到满足递归终止条件。然后根据具体问题，在递归的过程中进行一些操作和处理，实现对数据结构的遍历和搜索。通过不断地向下递归和返回，DFS算法能够有效地遍历或搜索图、树等数据结构。
回到本题，网格结构比树的结构复杂些，比图的结构简单些，我们先来看看树上是如何进行DFS遍历的 (以二叉树为例)。
二叉树的dfs遍历有分为前序、中序和后序遍历，大家应该都有所了解，这里就不做过多赘述，直接给出例子。
前序遍历（Preorder Traversal）：
- 首先访问根节点。
- 然后递归地前序遍历左子树。
- 最后递归地前序遍历右子树。
伪代码实现如下：
void preorderTraversal(TreeNode root) {
if (root == null) {
return;
}
访问根节点;
preorderTraversal(root.left);
preorderTraversal(root.right);
}
中序遍历（Inorder Traversal）：
- 首先递归地中序遍历左子树。
- 然后访问根节点。
- 最后递归地中序遍历右子树。
伪代码实现如下：
void inorderTraversal(TreeNode root) {
if (root == null) {
return;
}
inorderTraversal(root.left);
访问根节点;
inorderTraversal(root.right);
}
后序遍历（Postorder Traversal）：
- 首先递归地后序遍历左子树。
- 然后递归地后序遍历右子树。
- 最后访问根节点。
伪代码实现如下：
void postorderTraversal(TreeNode root) {
if (root == null) {
return;
}
postorderTraversal(root.left);
postorderTraversal(root.right);
访问根节点;
}
深入理解场景
二叉树的DFS（深度优先搜索）包含了两个重要的要素：
「访问相邻节点」和「判断终止条件」。
下面解释下这两个要素：
访问相邻节点：在DFS中，我们需要访问当前节点的相邻节点，也就是左子节点和右子节点。在递归函数中，我们会先处理当前节点的操作，然后再递归调用该函数访问左子节点和右子节点，实现对二叉树的深度优先遍历。
判断终止条件：在递归函数的开始部分，我们需要判断是否满足递归的终止条件，如果满足终止条件，直接返回或执行其他操作，结束递归过程。终止条件通常是当前节点为空（null），即遍历到叶子节点或空节点时，返回终止递归。这样可以确保递归不会无限进行，避免出现栈溢出等问题。
这两个要素共同构成了二叉树DFS的基本结构。通过递归地调用函数，我们可以实现前序、中序、后序等不同的DFS遍历方式。这种递归方式在解决二叉树相关问题时非常常用，可以帮助我们更好地理解二叉树结构，解决各种与二叉树相关的问题。
对比与二叉树的dfs我们可以推理出网格的dfs的要素：
首先，网格结构中的格子有上下左右四个。对于格子 (row, col) 来说，四个相邻的格子分别是 (row-1, col)、(row+1, col)、(row, coc-1)、(row, col+1)。换句话说，网格结构是「四叉」的。
其次，
网格 DFS 中的终止条件是什么？从二叉树的终止条件对应过来，应该是网格中不需要继续遍历、grid[r][c] 会出现数组下标越界异常的格子，也就是那些超出网格范围的格子，即对应二叉树的root==null的情况。值得一提的是，我们对于每个格子都进行了上下左右的判断，不管该格子是否在边界，就是先走如果超过了网格的范围再返回。
所以我们可以写出网格的dfs遍历的代码框架：
void dfs(int[][] grid, int r, int c) {
// 判断 base case
// 如果坐标 (r, c) 超出了网格范围，直接返回
if (!inArea(grid, r, c)) {
return;
}
// 访问上、下、左、右四个相邻结点
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
}这样是不是就没问题了呢？当然是有问题的，网格结构更像是一种简化的图结构，我们在遍历的时候可能会遇到之前遍历过的格子，为了避免一直在网格中‘’转圈圈‘’，我们需要标记之前的陆地格子，把值改为其他数值，比如2。之后我们就知道了哪些遍历过了。
所以每个格子都可能去3个值：
0-海洋、1-陆地（未到）、2-陆地（到过）
所以优化后的代码为：
void dfs(int[][] grid, int r, int c) {
// 判断 base case
if (!inArea(grid, r, c)) {
return;
}
// 如果这个格子不是岛屿，直接返回
if (grid[r][c] != 1) {
return;
}
grid[r][c] = 2; // 将格子标记为「已遍历过」
// 访问上、下、左、右四个相邻结点
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length
&& 0 <= c && c < grid[0].length;
}岛屿数量解答
看到这里我们就可以解答一下，岛屿数量的道题目了，代码如下：
public int numIslands(char[][] grid){
if (grid == null || grid.length == 0 || grid[0].length == 0) {
return 0;
}
int rows = grid.length;
int cols = grid[0].length;
int numIslands = 0;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if (grid[i][j] == '1') {
numIslands++;
dfs(grid, i, j);
}
}
}
return numIslands;
}
private void dfs(char[][] grid, int r, int c) {
int rows = grid.length;
int cols = grid[0].length;
if (r < 0 || r >= rows || c < 0 || c >= cols || grid[r][c] != '1') {
return;
}
grid[r][c] = '2'; // 将格子标记为「已遍历过」
// 继续向上、下、左、右四个相邻结点遍历
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}岛屿最大面积解答
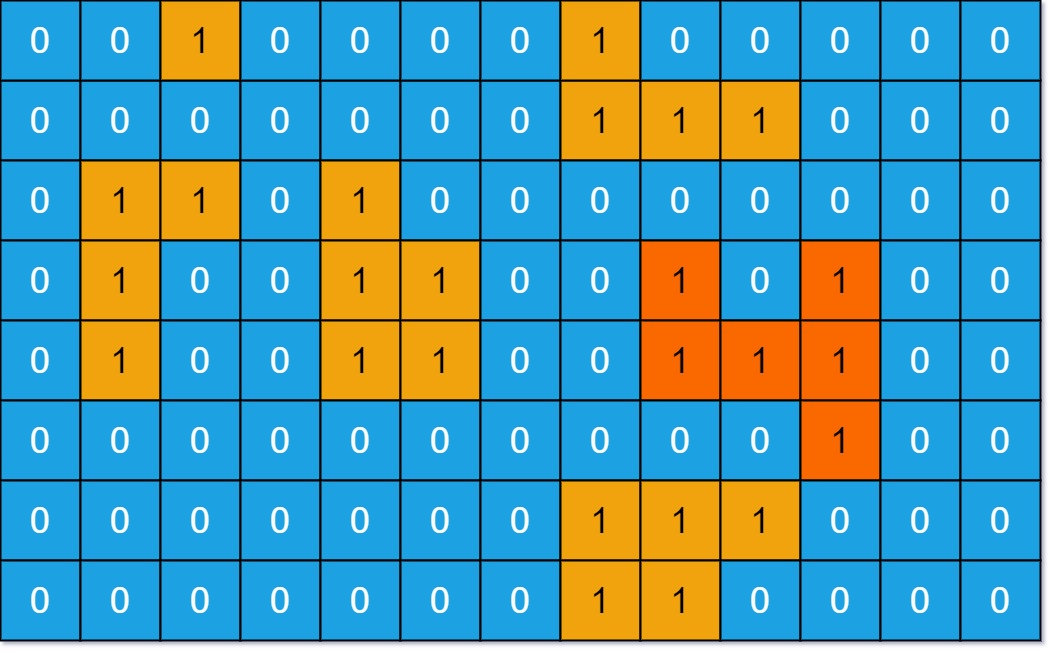
给你一个大小为
m x n的二进制矩阵grid。岛屿 是由一些相邻的
1(代表土地) 构成的组合，这里的「相邻」要求两个1必须在 水平或者竖直的四个方向上 相邻。你可以假设grid的四个边缘都被0（代表水）包围着。岛屿的面积是岛上值为
1的单元格的数目。计算并返回
grid中最大的岛屿面积。如果没有岛屿，则返回面积为0。
上图的结果返回为 6,即橙色部分。
这道题得核心就是计算每个岛屿的面积，在上面求岛屿数量的前提下，每遍历一个岛屿的格子就把面积加一即可。直接给出代码。
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int res = 0;
for(int r = 0;r < grid.length;r++){
for(int c = 0;c < grid[0].length;c++){
if(grid[r][c] == 1){
int a =area(grid,r,c);
res = Math.max(res,a);
}
}
}
return res;
}
int area(int[][] grid,int r,int c){
if(!inArea(grid,r,c)){
return 0;
}
if(grid[r][c] != 1){
return 0;
}
grid[r][c] = 2;
return 1 + area(grid,r-1,c)
+ area(grid,r+1,c)
+ area(grid,r,c-1)
+ area(grid,r,c+1);
}
boolean inArea(int[][] grid,int r,int c){
return 0 <= r && r < grid.length
&& 0 <= c && c < grid[0].length;
}
}岛屿的周长解答
给定一个
row x col的二维网格地图grid，其中：grid[i][j] = 1表示陆地，grid[i][j] = 0表示水域。网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。
岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。
看到这道题是否立即想到的 DFS？哈哈，其实对于这道题完全没必要，岛屿问题最容易让人想到BFS或者DFS，这里使用 DFS直接返回就是把简单问题搞复杂了。下面来讲解一下！
上面我们都了解了网格的dfs，在这道题中我们要求的是周长，是岛屿所有的 ‘边’ ，但是在dfs中我们不仅要求网格是否超过边界（root==null），还要考虑当前遍历的格子的状态（海洋还是没遍历过还是陆地）。设想一下，这些东西对我们解题有什么用？好像并没有啥用，反而会使问题复杂化。
再回到本题，要求周长，大致要求两类，一是与边界相邻的，一是与海洋相邻的。
当我们的 dfs 函数因为「坐标 (r, c) 超出网格范围」返回的时候，实际上就经过了一条边界边；而当函数因为「当前格子是海洋格子」返回的时候，实际上就经过了一条海洋边。这样，我们就把岛屿的周长跟 DFS 遍历联系起来了，代码如下:
public int islandPerimeter(int[][] grid) {
for (int r = 0; r < grid.length; r++) {
for (int c = 0; c < grid[0].length; c++) {
if (grid[r][c] == 1) {
// 题目限制只有一个岛屿，计算一个即可
return dfs(grid, r, c);
}
}
}
return 0;
}
int dfs(int[][] grid, int r, int c) {
// 函数因为「坐标 (r, c) 超出网格范围」返回，对应一条黄色的边
if (!inArea(grid, r, c)) {
return 1;
}
// 函数因为「当前格子是海洋格子」返回，对应一条蓝色的边
if (grid[r][c] == 0) {
return 1;
}
// 函数因为「当前格子是已遍历的陆地格子」返回，和周长没关系
if (grid[r][c] != 1) {
return 0;
}
grid[r][c] = 2;
return dfs(grid, r - 1, c)
+ dfs(grid, r + 1, c)
+ dfs(grid, r, c - 1)
+ dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length
&& 0 <= c && c < grid[0].length;
}其实我最开始想到的方法是遍历每一个空格，遇到岛屿，计算其上下左右的情况，遇到水域或者出界的情况，就可以计算边了。
s Solution {
// 上下左右 4 个方向
int[] dirx = {-1, 1, 0, 0};
int[] diry = {0, 0, -1, 1};
public int islandPerimeter(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int res = 0; // 岛屿周长
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
for (int k = 0; k < 4; k++) {
int x = i + dirx[k];
int y = j + diry[k];
// 当前位置是陆地，并且从当前位置4个方向扩展的“新位置”是“水域”或“新位置“越界，则会为周长贡献一条边
if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y] == 0) {
res++;
continue;
}
}
}
}
}
return res;
}最大人工岛解读
本题相比于以上几题较难，而且与本篇文章内容有些不符（超纲了啊！！！！），这里只讲解大致的思路具体的代码hxdm自己想吧~
这道题得不同是，我们可以(只能)将一个海洋(0)变成一个陆地(1)，然后求出最大的岛屿面积。计算岛屿的面积与上面的大致相同，需要注意的是我们要把构成岛屿的格子标记上该岛屿的面积，计算完成后然后再计算哪个格子变成海洋后，构成的岛屿面积最大。如图人工改造后最大岛屿为 7 + 3 + 3 = 13。
但是，直接这样做可能遇到一个问题，如果一个海洋格子，它的上下左右其中至少2个都与岛屿相邻，比如上图的三行三列那个0，岛屿面积不就成了1 + 7 + 7了 ？显然不是。这两个 7 来自同一个岛屿，所以填海造陆之后得到的岛屿面积应该只有 7+1=8。所以为了区分象上面那样的特殊情况，我们应该使用一个数组来确定海洋格子相连的岛屿是否为同一个。
所以本题的大致思路为，对网格做了两遍 DFS：第一遍 DFS 遍历陆地格子，计算每个岛屿的面积并标记岛屿；第二遍 DFS 遍历海洋格子，观察每个海洋格子相邻的陆地格子。
本文参考了 力扣 nettee 的思路，感谢大佬的分享！！！！
持续学习中！！！！
扫一扫
216
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
