算法通过村 | 第一关 | 白银挑战篇 中

文接上回，上次我们了解了两道高频的链表相关算法题及其解法，不知道上次我给的解答是否能够给各位大gei们带来一点帮助，当然也欢迎指出我的错误和不足，感谢大家的阅读。

那么我们继续趁热打个铁，继续学习一些关于链表的相关题目！

---

合并有序链表

题目链接： 21. 合并两个有序链表 - 力扣（Leetcode）

                   88. 合并两个有序数组 - 力扣（LeetCode） （相似题目）

题目详情：

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 

  示例1：

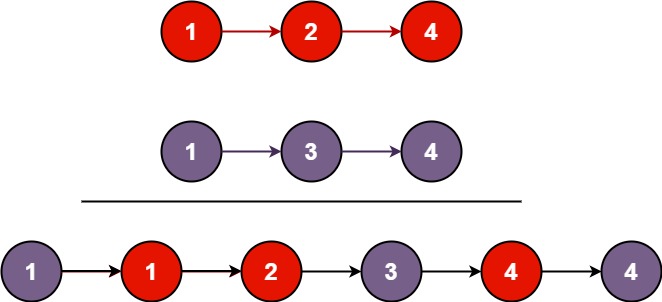
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

 对于这类合并且要求有序的题目，大体上有两种方法，一是创建一个新的链表，而是把一个链表的结点拆解到另一个链表上，除此之外还有一个递归法，其实就是第二种的延伸。

说到递归，可能很多人都很迷，总是被一些边界问题搞得很恶心，对于可以使用递归来解决的问题，主要要思考三点： 一是确定递归函数的参数和返回值，二是确定终止条件，再就是确定每一层递归的逻辑。之后我也会和你们一起学习递归的相关知识，后续会持续记录。

 

使用递归可能不太好想，但我就是想看看使用递归是如何解决该问题的：

        递归的思路是：比较两个链表头节点的值，将较小的节点作为合并后的链表的头节点，然后递归地合并剩余部分。

具体步骤如下：

1. 如果其中一个链表为空，直接返回另一个链表。
2. 然后，比较两个链表头节点的值，将较小的节点作为合并后的链表的头节点。
3. 接着，递归地调用 mergeTwoLists 方法，将较小节点的 next 指向递归调用的结果。
4. 最后，返回合并后的链表头节点。

递归解法的时间复杂度为 O(m+n)，其中 m 和 n 分别是两个链表的长度。递归过程需要遍历两个链表的所有节点。空间复杂度为 O(m+n)，递归调用会使用到系统栈空间。

 具体的代码如下：

class ListNode {
    int val;
    ListNode next;

    public ListNode(int val) {
        this.val = val;
        this.next = null;
    }
}

public class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        }
        if (l2 == null) {
            return l1;
        }

        if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }
}

递归可能不太好理解，我们来看看下面这种好理解的解答：

  public static  ListNode mergeTwoLists2(ListNode l1,ListNode l2){

        ListNode dummynode = new ListNode(-1);
        ListNode res = dummynode;
        while(l1 != null && l2 != null){
            if(l1.val < l2.val){
                dummynode.next = l1;
                l1 = l1.next;
            } else if (l1.val > l2.val) {
                dummynode.next = l2;
                l2 = l2.next;
            }else {
                dummynode.next = l1;
                l1 = l1.next;
                dummynode = dummynode.next;
                dummynode.next = l2;
                l2 = l2.next;
            }
            dummynode = dummynode.next;
        }

        while (l1 != null){
            dummynode.next = l1;
            l1 = l1.next;
            dummynode = dummynode.next;
        }
        while(l2 != null){
            dummynode.next = l2;
            l2 = l2.next;
            dummynode = dummynode.next;
        }
        return res.next;
    }

这里使用了一个名为 ‘虚拟头结点 ’的占位符，  如下所示：

 ListNode dummynode = new ListNode(-1);

        虚拟头结点的目的是简化链表的操作和处理边界情况。通常，链表的头结点会存储实际的数据，并且头结点可能需要在操作中被删除、插入或替换。这些操作可能导致特殊情况的处理，例如处理头结点时需要单独处理，或者需要使用条件判断来处理链表为空的情况。

        通过添加虚拟头结点，我们可以使所有的节点在操作中拥有一致的结构，即都有前驱节点，这样可以简化代码逻辑。虚拟头结点的存在使得链表的头结点永远存在，因此我们不需要特殊处理链表为空的情况。此外，虚拟头结点还能够保持链表的一致性，即链表始终有至少一个节点。

以上代码中括号内的数值是用于初始化虚拟头结点的值。不同的数值在使用时可以用来代表不同的含义，具体区别取决于程序的设计和使用场景。

通常，将虚拟头结点的值设置为特定的数值，如 -1、0 或其他常量，是为了标识虚拟头结点的特殊性，以与实际节点的值进行区分。

除以上两种方法外，还可以使用双指针来解题，这种方法就是我们在最开始说的前一种的延伸，

具体步骤如下：

1. 创建一个新的链表作为合并后的链表，使用两个指针分别指向两个链表的头部。
2. 比较两个指针所指节点的值，将较小值的节点连接到新链表中，并将对应指针后移一位。
3. 重复这个过程，直到其中一个链表遍历完毕。
4. 然后将剩余链表的部分直接连接到新链表的末尾。

代码如下：

class ListNode {
    int val;
    ListNode next;

    public ListNode(int val) {
        this.val = val;
        this.next = null;
    }
}

public class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(0);
        ListNode curr = dummy;

        while (l1 != null && l2 != null) {
            if (l1.val < l2.val) {
                curr.next = l1;
                l1 = l1.next;
            } else {
                curr.next = l2;
                l2 = l2.next;
            }
            curr = curr.next;
        }

        // 将剩余链表的部分连接到新链表的末尾
        if (l1 != null) {
            curr.next = l1;
        }
        if (l2 != null) {
            curr.next = l2;
        }

        return dummy.next;
    }
}

---

大概了解了几种不同的思路，那我们来尝试一下这道题目的拓展吧！

题目：23. 合并 K 个升序链表 - 力扣（LeetCode）

 这是一道困难的题，如果我们不了解合并两个有序链表的过程和实现，可能很难想到解决思路，如果硬要解的话，分治法和优先队列可以解决（但我不会。。。。。。）。

但我们了解了两个链表的合并，只要用之前的方法遍历一遍应该就行了，具体的代码就不展示了，这里只提供一个小思路。

还有一道相似的题目：1669. 合并两个链表 - 力扣（LeetCode）

 上面的如果懂了，那么这道题就没什么大问题了，主要就是遍历一下链表A ,找到链表A 删除a,b部分后的尾结点，还有链表B的尾结点，然后将链表连接即可。

具体的代码如下：

class ListNode {
    int val;
    ListNode next;

    public ListNode(int val) {
        this.val = val;
        this.next = null;
    }
}

public class Solution {
    public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {
        ListNode pre1 = list1, post1 = list1, post2 = list2;
        int i = 0, j = 0;

        // 寻找第 a-1 个节点和第 b+1 个节点
        while (pre1 != null && i < a - 1) {
            pre1 = pre1.next;
            i++;
        }
        while (post1 != null && j < b + 1) {
            post1 = post1.next;
            j++;
        }

        // 寻找 list2 的尾节点
        while (post2.next != null) {
            post2 = post2.next;
        }

        // 链接 list1 和 list2
        pre1.next = list2;
        post2.next = post1;

        return list1;
    }
}

解释如下：

1. 使用 pre1 指针来寻找第 a-1 个节点，使用 post1 指针来寻找第 b+1 个节点。
2. 然后，我们使用 post2 指针寻找 list2 的尾节点。
3. 最后，我们将 pre1 的 next 指向 list2，将 post2 的 next 指向 post1，完成链表的合并。
4. 返回合并后的链表 list1。

 之后会继续分享俺的算法学习之路！