多实例文章/方法学习记录_DTFDMIL

DTFD-MIL：组织病理学全切片图像分类的双层特征蒸馏多实例学习

> CVPR 2022 Oral | 代码已开源 GitHub

---

1 摘要（背景-挑战-方法-贡献）

维度	要点
背景	多实例学习（MIL）已成为仅有“切片级标签”的组织病理学全切片图像（WSI）分类的主流范式。
挑战	① 单张WSI尺寸巨大（108~109像素），实例（patch）数量极多；② 阳性区域占比小，且训练集“袋子”（slides）稀少 → 极易过拟合。
方法	提出双层特征蒸馏MIL（DTFD-MIL） 1. 将一张slide随机拆成若干“伪袋子”（pseudo-bags），虚拟增广袋子数量；2. Tier-1 AB-MIL 对伪袋做预训练，并首次在AB-MIL框架下推导出实例概率（Grad-CAM思想）；3. 按4种策略蒸馏伪袋特征，再送入Tier-2 AB-MIL 得到最终slide预测。
贡献	① 理论：给出AB-MIL实例概率解析式，结束“只能用attention分数近似”的历史；② 算法：伪袋+双层蒸馏策略，显著降低小样本过拟合； ③ 实验：在CAMELYON-16与TCGA-Lung两大公开集上AUC分别提升4.0%与1.2%，刷新SOTA。

---

2 引言（背景-挑战-研究现状-提出新方法-贡献）

2.1 背景

• 数字病理全切片（WSI）自动分析可大幅提升诊断效率，但像素级标注几乎不可行。
• 弱监督MIL天然契合：一张slide=bag，切分patch=instance，仅需slide级标签。

2.2 挑战

1. 数据方面：单张WSI生成数千~数万patch，而公开训练集往往<500张slide。
2. 算法方面：阳性区域占比极低（CAMELYON-16平均<5%），传统AB-MIL的attention分数会淹没弱信号。
3. 理论方面：AB-MIL被长期认为“无法显式计算实例概率”，只能用attention值做经验排序。

2.3 研究现状（领域脉络，非细节）

• 2015-2018：instance池化（max/mean）→ 效果差。
• 2018-今：bag-embedding成为主流，按attention生成方式可分为：经典AB-MIL、DS-MIL、CLAM、Trans-MIL等。
• 2021-今：开始引入互实例关系（GNN、Transformer）缓解小样本问题，但未触及“袋子数量不足”这一根本痛点。

2.4 提出新方法

我们换角度：不增加真实slides，而是“虚拟增广bags”——pseudo-bags；并借助推导出的实例概率做特征蒸馏，实现双层MIL。

2.5 本文贡献

1. 首次在AB-MIL框架内解析推导出实例属于正/负类的概率，为后续MIL研究提供通用工具。
2. 提出DTFD-MIL：pseudo-bag增广 + 双层特征蒸馏，系统性缓解小样本过拟合。
3. 在两大公开WSI数据集上取得新SOTA，代码开源便于社区扩展。

补充：关于ABMIL多实例中attention值的理解：

🎯 类比理解：评选优秀班级（bag=班级，patch=同学）

• 年级里有 50 个班级（50 个 bag）。
• 每个班级 50 名同学（50 个 patch）。
• 教务处只看班级最终称号（bag 标签：1=优秀班级，0=普通班级）。
• 评选规则：“只要班里有一名同学足够优秀，这个班级就记为优秀班级”（MIL 的 at-least-one）。

🎯 attention 值就是“每名同学的优秀得分”

• 让每位同学提交综合素质材料（patch 特征 hₖ：成绩、竞赛、志愿、体能…）。
• 年级组（小评委-实际由神经网络充当）读完材料，给每人打一个 0~5 分的“优秀指数”（logit）。
• softmax（指数放大差异 + 归一化成概率） → “优秀占比” aₖ，全班总和 = 1。
  aₖ 越高 → 这名同学越像让班级拿到优秀的关键人物。

同学	优秀占比 aₖ	通俗解释
小明	0.42	42 % 的“优秀理由”集中在他身上
小红	0.03	几乎看不出他对班级优秀的贡献

🎯 最终决策（bag 特征）

把每名同学的材料 hₖ 按“优秀占比”加权求和 → 得到班级综合档案
F = 0.42·h_小明 + 0.03·h_小红 + …
再用 F 预测班级是否优秀（bag 概率）。

🎯 训练时：占比会自动聚焦

• 如果班级真·优秀，但“优秀占比”分散，梯度下降会抬升真正优秀同学的占比，压低其他人。
• 如果班级普通，所有人的占比都会被压低（因为“只要有一人足够优秀就该评上”，现在没评上 ⇒ 目前最突出的同学也不够优秀）。

🎯 结果：aₖ 能当班级优秀热图

直接把 aₖ 染到对应同学座位 → 亮区 = 高占比 = 模型眼中“让班级优秀的关键学生”。

attention 值 aₖ 就是“评委网络”给每名同学打的“优秀贡献占比”，softmax 后成相对分数，加权求和得班级档案，训练时只靠班级标签反向传播，分数自动聚焦到真正让班级优秀的那几名同学。

---

3 相关工作

研究问题	代表方法	关键不足
Q1：如何聚合instance特征	① Max/Mean Pooling; ②RNN-MIL	① 丢失空间/语义关联； ②长序列梯度消失
Q2：如何学到更具判别性的bag-embedding	① Classic AB-MIL (Ilse et al. 2018);② DS-MIL (cosine attention);③ Trans-MIL (Transformer)	① 仅一个attention向量，鲁棒性差;② 需要额外对比学习，计算大;③ 模型参数量×10，小数据集更易过拟合
Q3：如何估计instance概率	① 直接用attention分数;② 事后grad-CAM可视化	① 非概率解释，阈值难定;② 离线工具，无法端到端优化

→ 文章同时解决Q2+Q3：推导实例概率并嵌入训练，再用pseudo-bag增广直击“bag数量不足”。

---

4 预先准备：输入输出约定

符号	含义
输入	一张slide X={x₁,…,x_K}，共K个256×256 patch（20×），仅知slide标签Y∈{0,1}。
中间	经ResNet50提取d=512维特征h_k=H(x_k)。
输出	slide级预测Ŷ∈[0,1]；如需要可输出patch级概率p_k^c。

---

5 方法（总-分结构）

5.1 总览

DTFD-MIL=“pseudo-bag增广 + 双层AB-MIL + 实例概率蒸馏”。

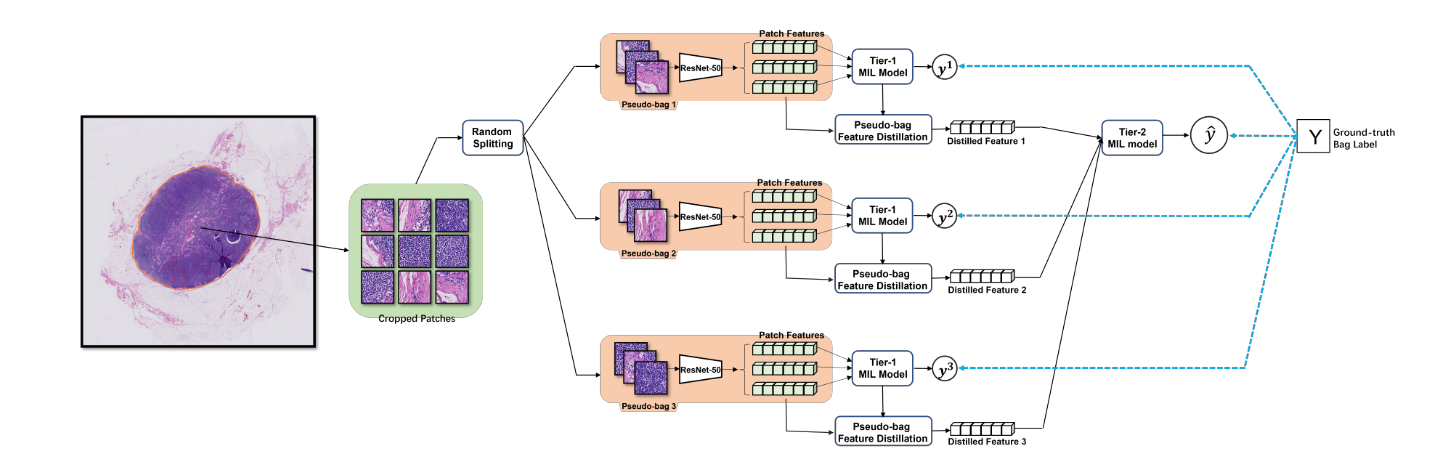
5.2 动机

• Tier-1：pseudo-bag数量↑ → 训练信号↑，但随机拆分会引入标签噪声（阳性slide的某pseudo-bag可能全阴）。
• Tier-2：用可解释的概率做特征蒸馏，把“可能阳性的patch”选出来再学一次，抑制噪声。

5.3 实例概率推导（理论核心）

命题1 AB-MIL是经典图像分类网络的一种特例 ⇒ 可直接套用Grad-CAM思想。
对第 k 个 instance，其 logit
$L_k^c={\sum }_d{\beta }_d^c\cdot {\hat{h}}_{k,d},{\beta }_d^c=\frac{1}{K}{\sum }_i\frac{\partial s^c}{\partial {\hat{h}}_{i,d}}$
其中 ${\hat{h}}_k=a_k\cdot K\cdot h_k$（attention 放大后特征）。

实例概率
$$p_k^c=\frac{\exp (L_k^c)}{{\sum }_t\exp (L_k^t)}$$
→ 端到端可导，可随网络一起训练。

5.4 双层框架详解

Tier-1 AB-MIL（伪袋级）

1. 将 slide X_n 随机划分为 M 个伪袋
   X_n¹,…,X_n^M，每袋约 K/M 个 patch。
2. 伪袋标签继承 slide 标签：Y_n^m = Y_n。
3. 对每个伪袋喂入 AB-MIL，得到袋级 logits
   s_n^m = AB-MIL({h_k | x_k ∈ X_n^m})。
4. 经 softmax 得伪袋概率
   y_n^m = σ(s_n^m) ∈ [0,1]。
5. 平均交叉熵损失
   L₁ = −1/(MN) Σ_n=1^N Σ_m=1^M [Y_n log y_n^m + (1−Y_n) log(1−y_n^m)]。
6. 同步用推导公式计算实例概率 p_k^c，为后续蒸馏做准备。

特征蒸馏策略（4选1）

策略	做法	适用场景
MaxS	选pseudo-bag内最大正类概率的instance特征	快，但对噪声敏感
MaxMinS	同时选最大+最小概率特征并拼接	给Tier-2更大边界，鲁棒↑
MAS	选attention分数最大的instance特征	与经典AB-MIL对齐
AFS	用attention加权平均得到bag特征	信息最完整，计算稍高

Tier-2 AB-MIL（slide级）

1. 输入：slide n 的 M 个蒸馏特征向量
   f̂_n¹,…,f̂_n^M ∈ ℝ^D′。
2. 再次作为袋喂入 Tier-2 AB-MIL，得到 slide 级 logit
   s_n = T₂({f̂_n^m}_m=1^M)。
3. softmax 输出 slide 概率
   ŷ_n = σ(s_n) ∈ [0,1]。
4. 平均交叉熵损失
   L₂ = −1/N Σ_n=1^N [Y_n log ŷ_n + (1−Y_n) log(1−ŷ_n)]。
5. 总体目标
   min_θ₁,θ₂ (L₁ + L₂)
   实际训练时分阶段：先固定 θ₁ 优化 L₁，再固定 θ₁ 优化 L₂（见原文 Alg.1）。

---

6 实验

6.1 数据集

名称	任务	阳性/总数	平均patch数	特点
CAMELYON-16	乳腺癌前哨淋巴转移	110/399	~12k	阳性区域<5%，极难
TCGA-Lung	肺鳞癌 vs 腺癌	352/752	~11k	阳性区域>30%，相对易

6.2 实验设置

• 骨架：ImageNet预训练ResNet50→512维特征。
• 数据：20×放大，256×256不重叠patch，OTSU去背景。
• 训练：Adam，lr=2e-4，batch=1 slide，M=5（伪袋数），早停20 epoch。
• 评价：AUC（主指标）、Acc、F1；95% CI / 4折交叉验证。

6.3 主实验结果

CAMELYON-16（表1）

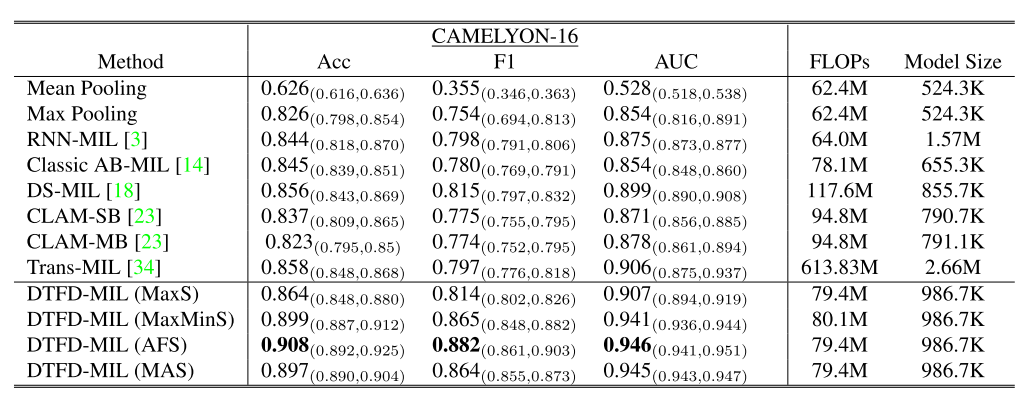
TCGA-Lung（表2）

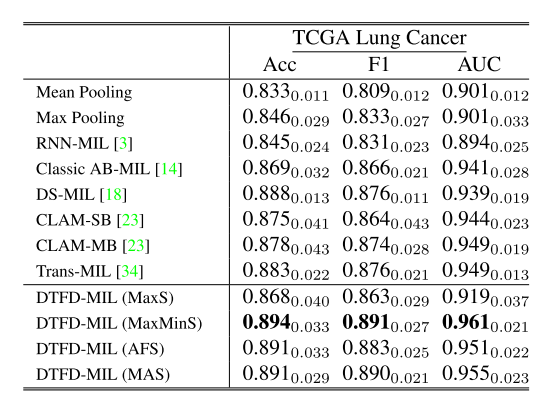
→ 在更难的小阳性数据集CAMELYON-16优势更显著，验证鲁棒性。

6.4 可视化分析（图4）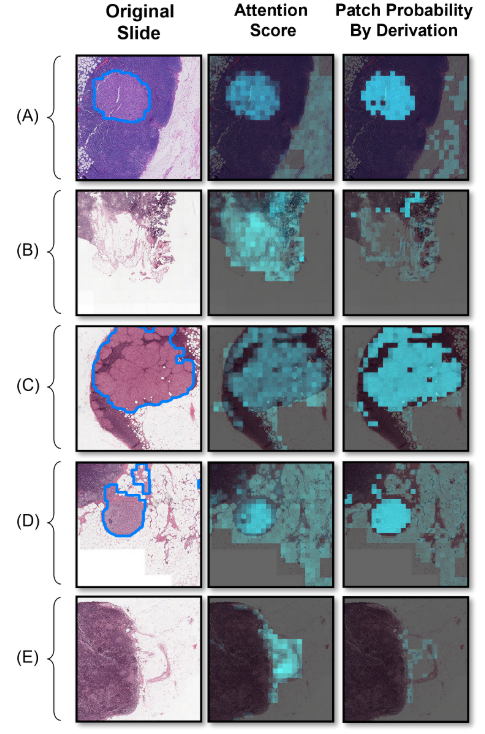

• attention热图：阴性slide出现大量假阳性激活。
• 实例概率热图：阳性区域高亮更集中，阴性区域假阳↓50%以上。
  ⇒ 证明推导概率比attention分数更可靠。

6.5 消融实验（图5-6）

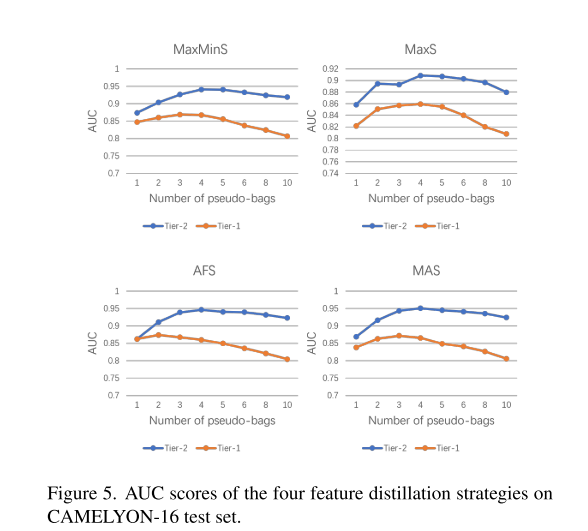
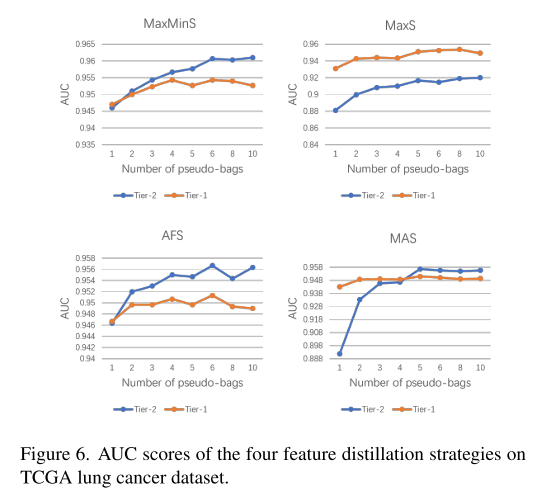
1. 伪袋数M：
   • CAMELYON-16：M≤5时Tier-2>AUC↑；M>5后Tier-1掉点明显（阳性patch被稀释）。
   • TCGA-Lung：肿瘤区域大，M=10仍稳定。
2. 蒸馏策略：
   • MaxS最差（单点易选到噪声）；MaxMinS/AFS/MAS相当，AFS略高。
3. 双层 vs 单层：
   • 同参数下，Tier-2平均带来**+2.3% AUC**增益，且收敛更快。

---

7 结论

• 背景：WSI-MIL的小样本与超大实例空间矛盾突出。
• 方法：我们提出实例概率解析公式+伪袋双层蒸馏DTFD-MIL，不增加标注、不暴涨参数。
• 效果：两大公开集新SOTA，实例概率热图可视化更可信。
• 展望：
  1. 实例概率工具可无缝嵌入其他AB-MIL变体（CLAM、Trans-MIL）；
  2. 探索自适应伪袋拆分（按组织语义或梯度方差）进一步降噪；
  3. 将DTFD思想扩展到弱监督分割、检测等更细粒度任务。

---

8 可直接引用的好句（中英对照）

场景	中文	英文原句
强调挑战	“单张WSI的像素量可达十亿级，而阳性病灶往往不足5%，这让‘袋子’极度稀疏，模型极易陷入局部极小。”	“The enormous size of WSIs together with the extremely low ratio of positive instances makes the optimizer prone to fall into local minima, leading to inferior generalization.”
引出贡献	“本文首次证明AB-MIL是经典图像分类框架的特例，从而结束了‘实例概率不可估’的长期假设。”	“We demonstrate that AB-MIL is a special case of the canonical CNN-MLP pipeline, enabling, for the first time, closed-form instance probability under the MIL umbrella.”
实验总结	“在CAMELYON-16这一‘小阳性区域’ benchmark上，DTFD-MIL将AUC从0.906提升至0.946，相当于把剩余错误率降低了42%。”	“On CAMELYON-16, DTFD-MIL improves AUC from 0.906 to 0.946, corresponding to a 42% reduction in remaining error—a substantial margin in medical imaging.”