水下二自由度舵机云台

---

前言

想给智能浮标的超声测距模块加一个云台，可以实现使其始终正对水底，不随水波干扰而晃动的功能，甚至可以实现扫描局部水域的功能。此项目不断完善中，纰漏、差错在所难免，会不断更新博文，更正错误。

---

一、理论基础

1.姿态的描述

坐标系

常用直角坐标系。

右手系

对直角坐标系X,Y,Z轴方向的一种规定：右手食指、中指、大拇指自然张开到90°，则其分别指向X,Y,Z轴方向。

两种最重要坐标系

• 对地坐标系（GCS）：取地面一点为原点，取北方为X方向，东方为Y方向，右手系原则确定地底为Z轴方向。设计这么一个坐标系的意义在于，可以假定地球是不动的，这样GCS就是固定的，其他变化的坐标系可以最后都转化到它这里进行融合。
• 机体坐标系（BCS）：取机体一点为原点。右手系原则规定X,Y,Z轴方向（怎么方便怎么来）。设计这么一个坐标系的意义在于，方便进行受力分析。无人机常采用B1坐标系：机头X，右翼Y，朝下Z。

坐标系转换矩阵

我们可以通过机体坐标系进行受力分析等工作，再把它转换到对地坐标系上，获得它对地面的姿态变化。同一个点在不同坐标系下可能有不同的坐标描述，坐标转换矩阵是实现不同坐标系间坐标值快速转换的工具。

我们这样看，先看二维的情况。假定刚开始机体坐标系XOY和地面坐标系xoy是重合的。然后机体绕Z轴方向逆时针转了$\theta$角。（逆时针符合右手定则：手握旋转轴，大拇指指向旋转轴正方向，四指握住的方向为绕此轴旋转的正方向，其实就是从此轴的正方向向负方向看时的逆时针方向）

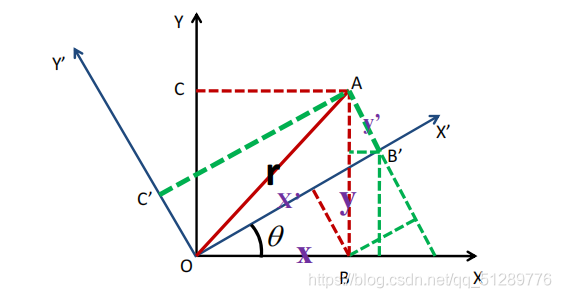
假设点A在XOY坐标系中坐标为（X,Y），在xoy坐标系中坐标为（x,y）。由三角函数关系易知，x = Xcos($\theta$)-Ysin($\theta$) , y = Xsin($\theta$)+Ycos($\theta$)

=
KaTeX parse error: Can't use function '$' in math mode at position 39: …n{bmatrix} cos($̲\theta$)& -sin(…
×
$$\begin{array}{c}\left[\begin{array}{c}X\\ Y\end{array}\right]\end{array}$$
好家伙，不会打公式，难到了我，等Letax差不多了回来更新。

2.姿态的解算

3.舵机的控制

4.二自由度云台控制算法

5.超声测距原理

五级标题

六级标题

二、工程实践

1.引入库

代码如下（示例）：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
import  ssl
ssl._create_default_https_context = ssl._create_unverified_context

2.读入数据

代码如下（示例）：

data = pd.read_csv(
    'https://labfile.oss.aliyuncs.com/courses/1283/adult.data.csv')
print(data.head())

该处使用的url网络请求的数据。

---

总结

提示：这里对文章进行总结：
例如：以上就是今天要讲的内容，本文仅仅简单介绍了pandas的使用，而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。