强化学习-值函数计算方法，值迭代和策略梯度等

目录

0.背景：

1.如何进行策略评估：

2.如何进行策略改进：

2.1值函数近似算法

2.2直接策略搜索

3.深度强化学习：

3.1DQN

3.2 AC/A2C/A3C（Asynchronous Advantage Actor Critic）

0.背景：

强化学习必不可少的三个步骤：策略执行（根据e贪婪/最大Q等得到下一跳动作）、策略评估（估计动作的Q值）、策略改进（找到最优策略）。

1.如何进行策略评估：

即值函数计算方法：

DP动态规划，需要已知环境模型。因为知道了模型（转移概率），所以不需要做实验。

蒙特卡洛：基于样本的方法。通过做实验，统计平均约等于真实的平均回报值。缺点是需要等待实验做完才能计算值函数。

时间差分：自举的思想，通过后一时刻的值，更新现在的值。可以实现在当下时刻就能计算值。

N bootstrap：n步的时间差分，介于蒙特卡洛和时间差分之间。

动态规划、蒙特卡洛、时序差分、n步bootstrap方法小总结_bootstrap 策略-优快云博客

2.如何进行策略改进：

2.1值函数近似算法

值迭代和策略迭代是强化学习中两种常用的寻找最优策略的方法。

策略迭代：需要策略评估（也就是1做的工作）和策略改进（更新Q值，V值）。也就是：

策略评估收敛->从头更新整个策略->用新策略再评估到收敛->再更新策略->......->最优策略。

优：迭代次数少      缺：计算复杂，策略收敛，但策略评估没收敛（见下方链接）

马尔科夫决策过程-策略迭代与值迭代(基于动态规划)_马尔科夫值迭代-优快云博客

值迭代：值函数收敛后，最后输出最优策略。图2所示，每次更新V的时候，不同于图1，用的是使得V最大的a，相当于及时做了隐式的策略改进，不需要等到本轮策略评估收敛。

策略评估->选当下最大Q继续策略评估->...->策略函数收敛->输出最优策略。

优：简单                 缺：迭代轮次增多。

2.2直接策略搜索

跳过值函数的步骤，直接进行最优策略的搜索。适用于连续动作空间。例如DDPG，这里我没用过，了解的不多。一般用优势函数更新策略网络。

3.深度强化学习：

DRL提升了RL在高维状态空间和连续动作空间的决策能力。一方面，深度网络的非凸函数拟合能力扩展策略的表征能力和强化学习方法的应用范围; 另一方面，深度网络强大的特征提取能力可使强化学习能处理视觉信息、声音信息等复杂输入。

3.1DQN

以前我总有个误区，就是直接策略搜索就是深度强化学习。NO!

像DQN啊，其实还是基于值函数的强化学习，因为它的本质还是更新Q值函数，只是用深度学习模型进行拟合。DQN就是比较入门级的深度强化学习模型。

【深度强化学习】(1) DQN 模型解析，附Pytorch完整代码_dqn模型-优快云博客

• 目标网络的意义，看上图的公式2，如果没有目标网络，目标Q值yi就一直是一个变化的值，让神经网络拟合一个一直变化的目标是很难收敛的的。

3.2 AC/A2C/A3C（Asynchronous Advantage Actor Critic）

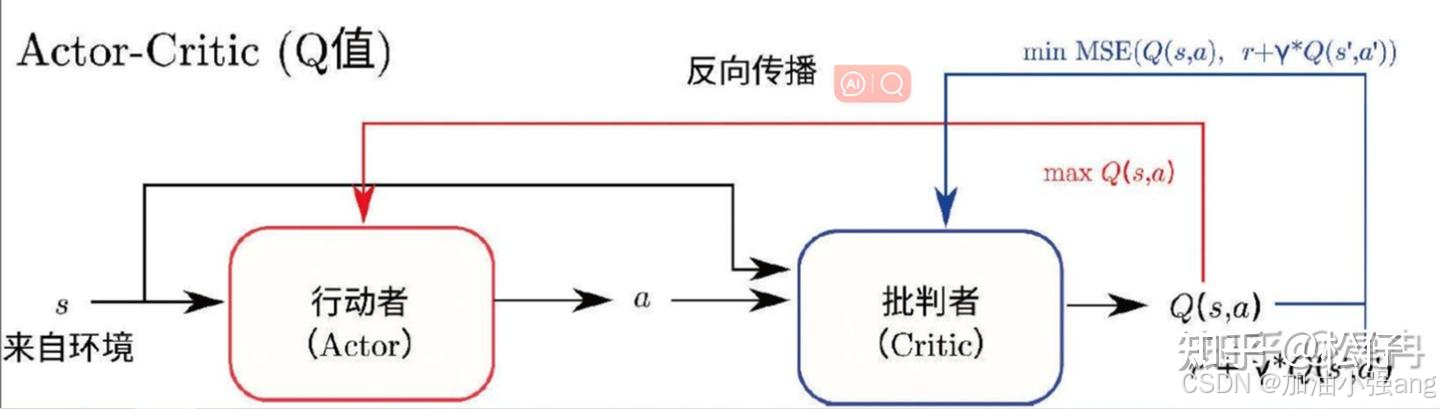
A3C也是经典的强化学习模型。它同时优化策略网络和值函数，是AC和A2C的加强版，收敛更快（因为并行与环境副本交互）。

强化学习中的 AC（Actor-Critic）、A2C（Advantage Actor-Critic）和A3C（Asynchronous Advantage Actor-Critic）算法_强化学习ac框架-优快云博客

• 优势函数：表达在状态s下，某动作a相对于平均而言的优势。

A3C中，用优势函数更新策略梯度，用值函数的差值更新Q值。我觉得这也类似一种广义的值迭代。

直接上伪代码：

【强化学习】14 —— A3C（Asynchronous Advantage Actor Critic）-优快云博客

附：

相比于深度学习，强化学习好在哪里呢？

深度强化学习（Deep Reinforcement Learning, DRL）和传统的深度学习（Deep Learning, DL）都是机器学习的重要分支，它们都利用深度学习的技术来处理复杂的数据和模式，但它们的应用场景和优势各有不同。这里主要介绍深度强化学习相对于传统深度学习的一些独特优势：

决策制定：

深度学习主要用于模式识别和预测任务，如图像和语音识别。而深度强化学习是为了使系统能够在没有明确指示的情况下作出决策。DRL通过与环境的交互来学习最佳行动策略，从而优化长期的奖励。

环境交互和自适应：

DRL能够在复杂的环境中进行学习，并能适应环境的变化。这使得DRL非常适合于那些需要实时决策的应用，如自动驾驶、机器人导航等。

处理不确定性：

强化学习特别适合于处理不确定性较高的环境。它不仅仅是在给定数据上进行训练，而是通过探索和利用策略来理解和适应环境的动态变化。

从少量或无标签数据中学习：

与深度学习不同，深度强化学习不需要大量标注数据。它可以通过与环境的交互获得反馈，这种反馈作为奖励信号，指导算法调整其行为策略。

长期目标和复杂策略的优化：

DRL强调的是如何根据当前行动的长期后果来做出决策。这对于那些需要考虑未来回报的任务非常有用，如金融投资、游戏策略等。

总之，尽管深度强化学习和深度学习都需要通过训练过程来达到模型的收敛，但深度强化学习在处理需要决策制定、环境交互以及长期目标优化的复杂问题时显示出独特的优势。这使得它在许多现实世界的应用中非常有价值，尤其是在那些传统深度学习方法难以解决的领域。