深度强化学习做光网络资源分配-动作数量动态变化

背景：

深度强化学习以其可以自动学习特征和强大的拟合能力的特点，已经被应用于各个领域。

对于一个标准化的强化学习，动作空间的数量应该是确定的。但是也有很多场景，候选动作的数量是动态变化的，譬如光网络中的选路，举个例子，如果将当前所在节点视为状态，如果有两个节点和它相连，那下一跳的候选动作数是2，转移到新状态后，如果有三个节点和它相连，候选动作数又变成了3。

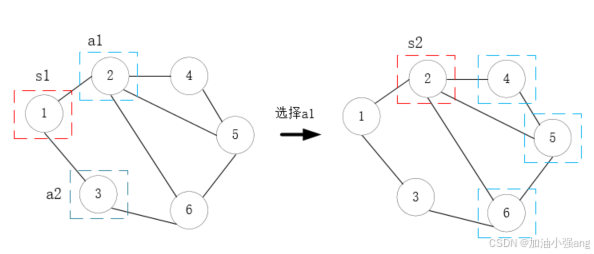
我们首先要知道，深度强化学习的输入和输出是什么。如附录中所示。

解决方法：

https://www.zhihu.com/question/417134029 来自这篇知乎

①如果单步状态下动作空间维度的最大值可知，则将该最大值当做动作空间，在学习时根据状态对不同的动作做mask，相当于做一个invalid action的学习；

解决方法如果想要soft constraint，即直接训练，当算法给到不能选的动作就给一个很差的收益，如果想要hard constraint, 那就是“屏蔽”（”mask out“）无效的操作，仅从有效操作中进行采样，然而这一过程仍未得到充分的研究。

②如果单步状态下动作空间维度的最大值未知，可能需要重新设计动作空间，如将离散动作空间连续化，在连续动作空间上学习，再将连续动作映射回每步对应的离散动作空间。

《 A Closer Look at Invalid Action Masking in Policy Gradient Algorithms》

回到我们的问题：

使用Q表对于此类问题较为好解决，相当于直接屏蔽无效解，但是，对于深度强化学习来说，不论是什么状态，输出的都是一个等长的向量。那么，如果使用DQN等模型，我们需要将其长度补齐。

怎么补齐：

怎么让智能体避开实际不存在的动作又不至于不收敛。

因为神经网络的输出维度是固定的，因此我们选择网络中的最大连接度，作为动作空间的维度。

有些动作是无效的，可以通过mask的方式，对无效动作进行掩蔽，加快网络收敛。

https://zhuanlan.zhihu.com/p/538953546

多智能体强化学习(二) MAPPO算法详解-优快云博客

连续动作空间的模型可以解决离散的问题吗？

对于PPO这种输出是随机策略的模型，是可以另其输出动作概率来进行离散动作的选择。但是对于DDPG这种确定性策略，就难以解决离散问题。

本人遇到一些概念的厘清：

对于机器学习中的一些概念。一般以回归问题为例，先定义损失函数，1.Loss 损失，实际输出和预期的差异。2.反向传播，误差反方向乘系数向前传递。3.梯度下降，做参数更新的方法，有很多种方法。优化器就是控制怎么梯度下降的。4.逻辑回归，softmax回归是什么？都用于进行归一化。而逻辑回归一般用于多分类问题，而softmax则用于二分类，因为只有一个输入神经元。

强化学习中的策略梯度：谁的梯度，要更新谁？回报R的梯度，要更新actor，或者critic神经网络参数。因为求的是最大回报，因此，是梯度上升。

对于Q-learning来说，损失函数是最小均方误差。

对于PPO来说，损失函数可详见推导。零基础学习强化学习算法：ppo_哔哩哔哩_bilibili

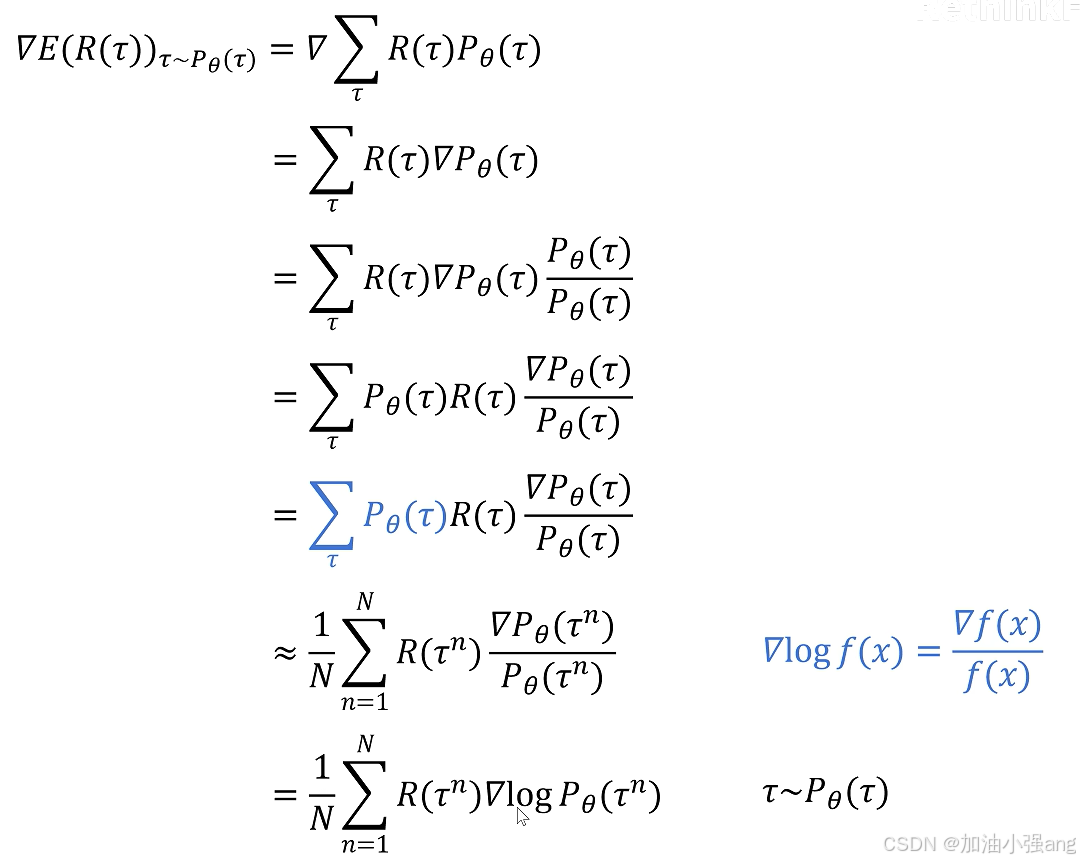
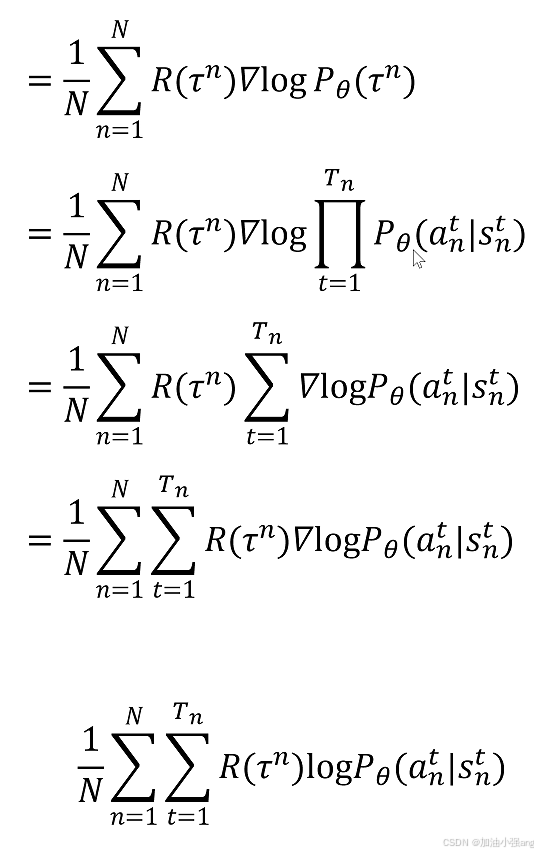
基于策略搜索的强化学习算法通常更倾向于on-policy方式，而基于值函数的算法则更加灵活，既可以采用on-policy方式，也可以采用off-policy方式。

• 直接对策略进行参数化表示和优化，因此通常需要对当前策略产生的样本进行充分利用，以确保策略的稳定性和收敛性。在训练过程中，如果频繁更换策略（即采用off-policy方式），可能会导致策略的不稳定性和难以收敛。
• 值函数本身并不直接依赖于策略，而是依赖于状态和动作，因此可以使用由不同策略产生的样本来更新值函数。这使得基于值函数的算法能够更容易地实现off-policy学习，从而利用更多样化的数据来改进策略。

附：强化学习模型的输入和输出

离散动作空间

1. Q-Learning

   • 输入：当前状态s和可选动作集合A。
   • 输出：在状态s下采取每个动作a的预期回报值Q(s, a)。

2. Deep Q-Network（DQN）

   • 输入：当前状态s（通常是一个向量或矩阵，表示环境的状态信息）。
   • 输出：在状态s下采取每个可能动作a的Q值（即预期回报值），通常是一个向量，向量的长度等于动作空间的大小。

3. Double Q-Learning

   • 输入：与Q-Learning相同，为当前状态s和可选动作集合A。
   • 输出：在状态s下采取每个动作a的预期回报值，但使用了两个独立的Q函数来减轻过估计问题。

4. SARSA（State-Action-Reward-State-Action）

   • 输入：当前状态s、当前动作a、奖励r、下一个状态s'和下一个动作a'（这些信息通常在算法迭代过程中获得）。
   • 输出：更新后的Q值表或Q函数，用于描述在给定状态下采取某个动作的预期回报。

连续动作空间

1. Deep Deterministic Policy Gradient（DDPG）

   • 输入：当前状态s（通常是一个向量或矩阵，表示环境的状态信息）。
   • 输出：一个确定性的动作a，这个动作是通过神经网络计算得到的，表示在当前状态下智能体应该采取的最优动作。
   • 注：DDPG的核心思想是学习一个确定性策略，而不是随机策略。这使得代理系统更容易收敛到最佳策略。此外，DDPG还使用经验回放，将过去的经验存储在缓冲区中，并随机抽样用于训练，以减少样本相关性，提高学习效率。

同时适用

1. Actor-Critic

   • 输入：当前状态s（对于Actor）和当前策略下的动作a及状态转移信息（对于Critic）。
   • 输出：Actor输出下一个要采取的动作a'，Critic输出为动作概率（对于离散动作空间而言）或者动作概率分布参数（对于连续动作空间而言）。

2. Trust Region Policy Optimization（TRPO）

   • 输入：当前策略π和一组状态-动作对（s, a）。
   • 输出：更新后的策略π'，该策略在保持策略稳定性的同时尽可能提高回报。

3. Proximal Policy Optimization（PPO）

   • 输入：与TRPO类似，为当前策略π和一组状态-动作对（s, a）。
   • 输出：更新后的策略π'，该策略通过限制策略更新的幅度来保持稳定性，并同时提高回报。
   • 强化学习（3） PPO pytorch实例-优快云博客 PPO引入了重要度的概念，令off-policy模拟on-policy

4. Soft Actor-Critic（SAC）

   • 输入：当前状态s和可选动作集合A（或动作空间的连续表示）。
   • 输出：一个概率分布π(a|s)，表示在给定状态s下采取每个动作a的概率。SAC算法通过最大化策略的熵来平衡探索和利用。

注：离散vs连续：

对于离散动作空间来说，可以使用Q-Learning或者DQN来进行更新，计算出每一个候选动作的Q值，但当动作空间维度增多或者连续，就难以使用这种方法。

策略梯度的方法：

在一些连续场景，如金钱，方向等，难以使用离散的方式进行选择。可以使用策略梯度的方法，直接进行策略搜索。

注：随机策略vs确定策略

随机策略：如Q-learning使用E-greedy进行随机；如PPO输出的是动作的概率，使用正态分布对动作进行采样选择，即每个动作都有概率被选到

确定策略：如DDPG策略输出即是动作。如果想增加强化学习中的探索，可以加入噪声。

后续待解决：

多智能体深度强化学习选路的难点：

1.多智能体不同时到达终点状态。对每个agent加一个是否到达终点的状态信息。解决：用dones矩阵表示。

2.随着状态的变化，动作空间动态变化。解决：动作空间维度 = 网络拓扑中最大连接度

MDRL中，如QMIX具体是怎么更新模型的，底层用Q-learning不行吗？

QMIX和MAPPO都是中心计算，分布执行的模型，每个agent根据自己的局部观测给出action，中心计算模型，将每个agent的action拼接起来，计算整体的v值，更新价值网络。QMIX底层是DQN，维护自己的Q神经网络。感觉底层是可以用Q-learning的，因为Qmix是根据输入的Q值计算的联合动作Q。

以下为MAPPO的伪代码。每个agent都把全局动作的奖励看做自己当前动作的奖励。

【MADRL】多智能体近端策略优化（MAPPO）算法_mappo算法-优快云博客