树
树的定义:树(Tree)是n(n>=0)个结点的有限集。n=0时称为空树。在任意一棵非空树中:(1)有且只有一个特定的称为根(Root)的结点;(2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2…Tm,其中每个集合本身又是一颗树,并且称为根的子树(SubTree):

二叉树
二叉树(Binary Tree)是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别为根结点的左子树和右子树的二叉树组成。
二叉树的顺序存储适用性不强,链式存储结构比较方便操作,也称二叉链表。
二叉树的二叉链表结点结构定义:
typedef struct Node
{
char data;
struct Node *l;//左子树
struct Node *r;//右子树
}Node;
二叉树的遍历方法有四种,分别是:前序遍历,中序遍历,后序遍历和层次遍历。
前序遍历(左右根):若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树:

代码如下:
void frontprint(Node *T)//前序遍历输出
{
if(T==NULL)
return;
else
{
lastprint(T->l);//先前序遍历左子树
lastprint(T->r);//再前序遍历右子树
printf("%c",T->data);
}
}
中序遍历(左根右):

代码如下:
void midprint(Node *T)//中序遍历输出
{
if(T==NULL)
return;
else
{
midprint(T->l);//中序遍历左子树
printf("%c",T->data);
midprint(T->r);//最后中序遍历右子树
}
}
后序遍历(左右根):
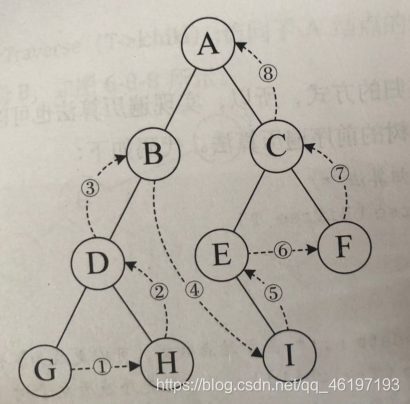
代码如下:
void lastprint(Node *T)//后序遍历输出
{
if(T==NULL)
return;
else
{
lastprint(T->l);//先后序遍历左子树
lastprint(T->r);//再后续遍历右子树
printf("%c",T->data);
}
}
层序遍历(需要用到队列):若树为空,则空操作返回,否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。
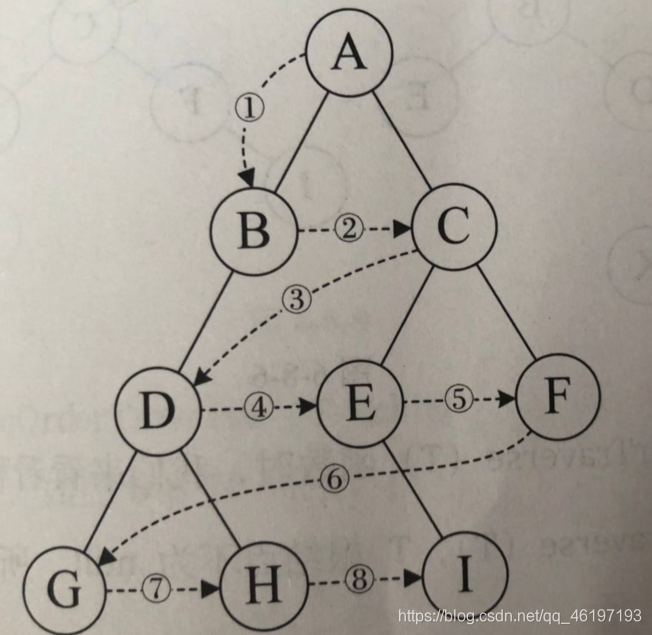 代码如下:
代码如下:
Node *ans[1000],*flag;
int a=0,b=1;
if(head!=NULL)
{
ans[0]=head;
while(a!=b)
{
flag=ans[a++];
printf("%c",flag->data);
if(flag->l!=NULL)//判断有没有左子树
ans[b++]=flag->l;
if(flag->r!=NULL)//判断有没有右子树
ans[b++]=flag->r;
}
}
二叉搜索树
一棵二叉树,可以为空;如果不为空,满足以下性质:1、非空左子树的所有值小于其根结点的值。
2、非空右子树的所有值大于其根结点的值。
3、左、右子树都是二叉搜索树。
二叉搜索树的查找操作(查找效率取决于树的高度):查找从根结点开始,,如果树为空,返回NULL;如果搜索树非空,则根结点的值和X进行比较,并进行不同处理:1、若X小于根结点的值,只需在左子树中继续搜索;
2、如果X大于根结点的值,在右子树中继续进行搜索;
3、若两者比较结果是相等的,搜索完成,返回指向此结点的指针。
代码如下:
int Find(int x,Build Tree)
{
if(Tree==NULL)//树为空,查找失败
return NULL;
if(x>Tree->data)
return Find(x,Tree->Right);//在右子树继续查找
else if(x<Tree->Data)
return Find(x,Tree->Left);//在左子树中继续查找
else if(x==Tree->Left);
return Tree;//查找成功,返回找到的结点的地址
}
二叉搜索树找最小值:
int Findmin(Build Tree)
{
if(Tree==NULL)//若二叉树为空,返回NULL
return NULL;
else if(Tree->Left==NULL)
return Tree;//找到最左叶结点并返回
else
return Findmin(Tree->Left);//沿左分支继续查找
}
二叉搜索树找最大值:
int Findmax(Build Tree)
{
if(Tree!=NULL)
{
while(Tree->Right!=NULL)
Tree=Tree->Right;
}
return Tree;
}
二叉搜索树的插入:关键是要找到应该插入的位置,然后采用与Find类似的方法。
Build Insert(int x,Build Tree)
{
if(Tree==NULL)//如果树为空,则生成一个只有一个结点的二叉搜索树
{
Tree=malloc(sizeof(struct Node));
Tree->Data=x;
Tree->Left=Tree->Right=NULL;
}
else//开始找x所插入的位置
{
if(x<Tree->Data)
Tree->Left=Insert(x,Tree->Left);//递归插入左子树
else if(x>Tree->Data)
Tree->Right=Insert(x,Tree->Right);//递归插入右子树
}
return Tree;
}
二叉搜索树的删除:
三种情况:1、要删除的是叶结点:直接删除,并再修改其父结点指针指向NULL;
2、要删除的结点只有一个子结点:将其父结点的指针指向要删除结点的
子结点。
3、要删除的结点有左右两棵子树:用另一结点替代被删除的结点:右子树的最小元素或者左子树的最大元素。
平衡二叉树
在任一结点左右子树高度差的绝对值不超过1;
如下图:
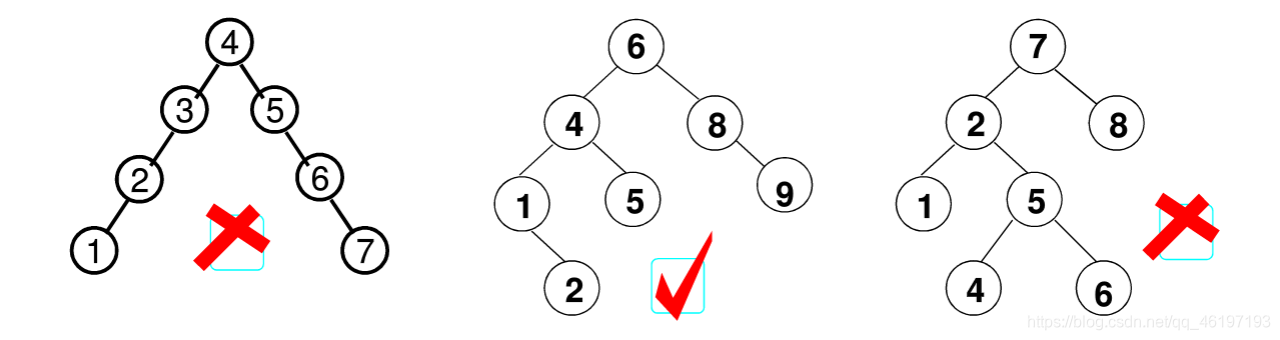







 本文介绍了树的定义,强调了根节点和子树的概念。接着详细讲解了二叉树的特性,包括二叉链表结构、四种遍历方法(前序、中序、后序和层次遍历)的实现。此外,还探讨了二叉搜索树的性质,查找、插入和删除操作,以及平衡二叉树的概念,为理解数据结构中的树形结构提供了全面的介绍。
本文介绍了树的定义,强调了根节点和子树的概念。接着详细讲解了二叉树的特性,包括二叉链表结构、四种遍历方法(前序、中序、后序和层次遍历)的实现。此外,还探讨了二叉搜索树的性质,查找、插入和删除操作,以及平衡二叉树的概念,为理解数据结构中的树形结构提供了全面的介绍。
















 1592
1592

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








