凸优化基础知识

任务要求：

1、计算几何是研究什么的？
2、计算几何理论中（或凸集中）过两点的一条直线的表达式，是如何描述的？与初中数学中那些直线方程有什么差异？有什么好处？(按自己的体会)
3、凸集是什么？ 直线是凸集吗？是仿射集吗？
4、三维空间中的一个平面，如何表达？
5、更高维度的“超平面”，如何表达？
6、什么是“凸函数”定义？什么是Hessian Matrix 矩阵? 如何判别一个函数是凸函数？f(x)=x^3 函数是凸函数吗？
7、什么是“凸规划”？如何判别一个规划问题是凸规划问题。下例是凸规划问题吗？

1.计算几何研究方向

计算几何是指的对几何外形信息的计算机表示、分析和综合。
1.几何外形信息
那些用来确定某些几何外形的离散数据点或特征多边形
2.计算机表示
按照给定的信息，建立一定的数学模型，再通过计算机进行计算，求得其他所需的信息
3.分析和综合
对所建立的数学模型特性及误差等进行分析、综合，以便逼真地反映出几何形体

2.直线表达方式

在任意维度中，由两点P0、P1定义的直线参数方程式，当参数s为实数且u=P1-P0为直线的方向向量时可以表示为P(s) = P0 + s (P1-P0) = P0 + su
初中表达方式：
（1）设直线l上的两点P1、P2的坐标分别为(x1,y1)、(x2,y2)，且(x1≠x2)
所以直线l的斜率K：

（2）在直线l上任意取一点P（x，y）
将直线l的斜率K，P点的坐标代入直线的点斜式方程y-y1=k(x-x1)中得：

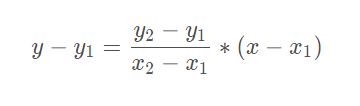
3、凸集是什么？ 直线是凸集吗？是仿射集吗？

凸集是在凸组合下闭合的仿射空间的子集。更具体地说，在欧氏空间中，凸集是对于集合内的每一对点，连接该对点的直线段上的每个点也在该集合内。

直线不是凸集；

仿射集亦称仿射流形、线性流形、仿射簇，是实线性空间中的一类子集。直线是仿射集。

4、三维空间中的一个平面，如何表达？

1.一般式：Ax+By+Cz+D=0

2.点法式（给出平面的一个法向量）：(x0,y0,z0)+k(x1,y1,z1)

3.截距式方程 ：x/a+y/b+z/c=1

4.法线式方程 ：xcosα+ycosβ+zcosγ=p

5、更高维度的“超平面”，如何表达？

超平面是指n维线性空间中维度为n-1的子空间。它可以把线性空间分割成不相交的两部分。比如二维空间中，一条直线是一维的，它把平面分成了两块；三维空间中，一个平面是二维的，它把空间分成了两块。

6、什么是“凸函数”定义？什么是Hessian Matrix 矩阵? 如何判别一个函数是凸函数？f(x)=x^3 函数是凸函数吗？

凸函数：凸函数就是一个定义在某个向量空间的凸子集C（区间）上的实值函数。

Hessian Matrix 矩阵：Hessen矩阵是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。
如何判别一个函数是凸函数？f(x)=x^3 函数是凸函数吗？
答：
（1）对于一元函数f(x)，我们可以通过其二阶导数f′′(x) 的符号来判断。如果函数的二阶导数总是非负，即f′′(x)≥0 ，则f(x)是凸函数.
（2）对于多元函数f(X)，我们可以通过其Hessian矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵，则是f(X)凸函数。
判断：根据一元函数如何判断该函数是否是凸函数，f’’(x)=6x，当x<0时，f’’(x)<0;当x>0时，f’’(x)>0,不满足函数的二阶导数总是非负，所以f(x)=x^3不是凸函数。

7、什么是“凸规划”？如何判别一个规划问题是凸规划问题。下例是凸规划问题吗？

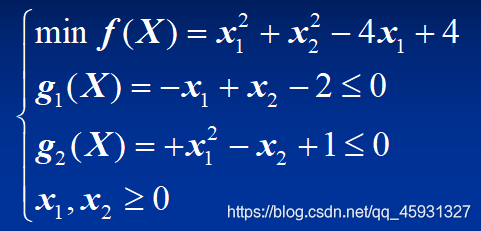
推导过程：