LeetCode 300.最长递归子序列-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_45888932/article/details/123458326

本文探讨了如何使用动态规划(DP)解决LeetCode上的最长递增子序列(Longest Increasing Subsequence)问题。作者首先尝试了未使用备忘录的递归方法，但在边界处理上遇到问题。接着，作者介绍了两种备忘录DP解决方案：一种是自底向上的迭代，另一种是从递归转换为迭代的方法。通过这两种方式，有效地避免了重复计算，提高了算法效率。博客总结了从递归到迭代的转换过程，并强调了DP在解决此类问题中的重要作用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

链接：https://leetcode-cn.com/problems/longest-increasing-subsequence/

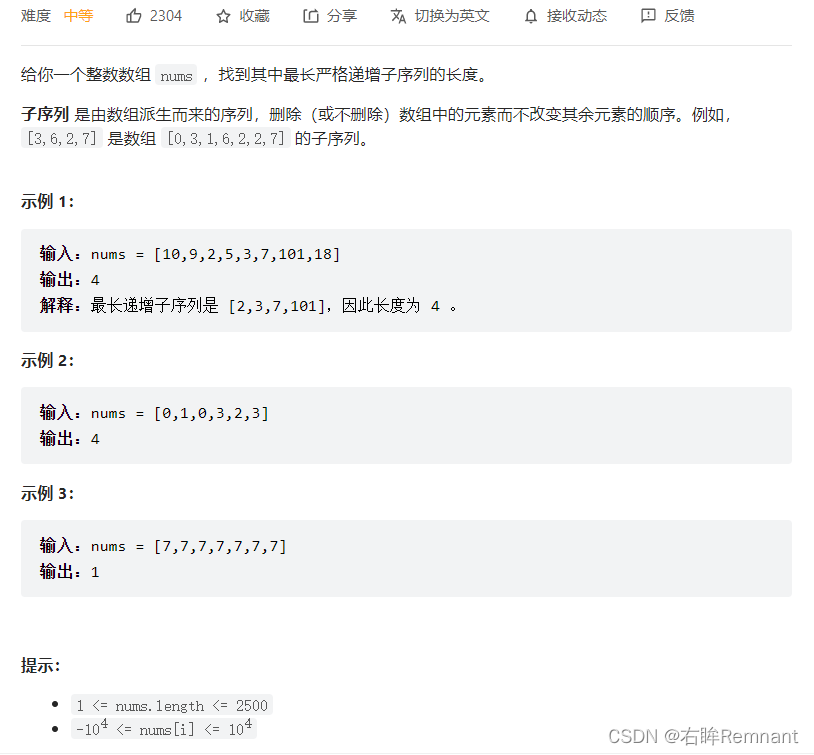
思路：

知道这是个典型的dp问题，但是想先用不加备忘录的递归写一下，但是边界不知道什么问题总是会差一；最后直接用了备忘录写的。

我要求什么：最长递增子序列 -》以index结尾的最长递增子序列

        状态：f(index) 最大值

        选择：当前位置选 or 不选

        转移方程： f(index) = Math.max(f(index), f(index - 1))

方案一：备忘录

class Solution {
  
    private int[] memo;
    public int lengthOfLIS(int[] nums) {
        memo = new int[nums.length + 1];
        Arrays.fill(memo, -66);
        lengthOfLISHelp(nums, nums.length - 1);
        
        int res = -1;
        for (int ele : memo) res = Math.max(res, ele);
        return res;
    }
    public int lengthOfLISHelp(int[] nums, int index) {
        if (index < 0) return 1;
        if (memo[index] != -66) return memo[index];

        memo[index] = lengthOfLISHelp(nums, index - 1);
        int res = 1;
        // 寻找前面小于index的数
        for (int i = index - 1; i >= 0; i--) {
            if (nums[i] < nums[index]) {
                res = Math.max(res, lengthOfLISHelp(nums, i) + 1);
            }
        }
        memo[index] = res;
        return res;
    }
}

方案二：dp

class Solution {
 
    private int[] memo;
    public int lengthOfLIS(int[] nums) {
        memo = new int[nums.length + 1];
        for (int i = 0; i < nums.length; i++) {
            memo[i] = 1;  // 初始化
            // 寻找前面小于index的数
            for (int j = 0; j < i; j++) {
                if ( nums[j] < nums[i]) {
                    memo[i] = Math.max(memo[i], memo[j] + 1);
                }
            }
        }
        
        int res = -1;
        for (int ele : memo) res = Math.max(res, ele);
        return res;
    }
}

总结：从递归 -》迭代的过程，递归函数本身表示一层循环，然后将递归函数主体作为内层循环即可。