(一）Acwing基本算法笔记

最新推荐文章于 2025-08-06 17:01:48 发布

一只没有情感的机器猪

最新推荐文章于 2025-08-06 17:01:48 发布

阅读量999

点赞数 26

CC 4.0 BY-SA版权

文章标签：算法笔记数据结构

本文链接：https://blog.youkuaiyun.com/qq_45768060/article/details/126072550

排序

添加链接描述

二分

二分有两类，整数二分比较难顶，要仔细处理边界问题

有单调性一定可以二分，但是没有单调性不一定不可以二分
二分本质性是二段性，一段满足，一段不满足；每次选择答案所在的区间，但区间长度为1时，就是答案所在了。
二分一定是要保证有解的，无解与题目有关；二分之后可以判断出原问题无解，而不是二分本身无解

对于模板的记忆要点

if的判断条件是让mid落在满足你想要结果的区间内
如果是左边界等于mid，即 l=mid，则mid = l+r+1/2,要加1；
如果右边界等于mid，即r=mid1，则mid=(l+r)/2，不要加1
为什么？主要是整数二分中会向下取整的原因，当 l和r相差1，即l=r-1时，如果不加1，mid就等于l，所以就没变就死循环了
如果前面是l=mid，后面就是r=mid-1;
如果前面是r=mid,后面就是l=mid+1;
都是左闭右闭

做题思路：先写好基本模板；然后看check的性质，观察怎么取区间；根据"满足性质” 条件下是要向左逼近(r=mid)，还是向右逼近（l=mid），去选择两个版本的代码，是否需要补偿+1；

帮助理解的链接：https://www.acwing.com/blog/content/346/

代码模板

这两个模板解决的是找>=||<=||>||< 某个数的
最左或最右的位置但这个数不一定在二分的数组中
如果在就能准确找到
如果不在找到的就是最接近答案的数（你要找大于等于5的第一个数）但数组中没有5 那找到的就是6的位置(如果有6的话)
所以二分是一定有答案的
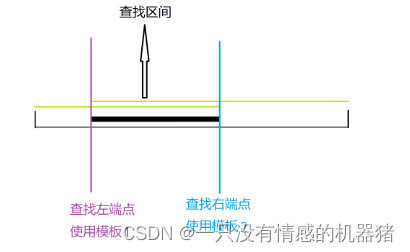
在这里插入图片描述

版本1

int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

版本2
当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。

int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

数的范围

寻找第一个和最后一个值为k的位置

#include<iostream>
using namespace std;
const int  N = 1e5+10;
int n,m,q,k;
int a[N]; 
int main(){
	cin >> n >> q;
	
	for(int i=0;i<n;i++){
		cin >> a[i];
	} 
	while(q--){
		int x;
		cin >> x;
		//起始位置：第一个大于等于x的数，所以要不断往左逼近；往左逼近，条件就要设为<=x
		int  l=0,r=n-1;
		while(l < r){
			int mid = l + r >> 1;
			if(a[mid] >= x) r=mid; //往左边逼近 
			else l = mid + 1;
		} 
		if(a[l] == x){
			cout << l << " ";
		} 
		else{
			cout << "-1 -1"<<endl;
			continue; 
		}
		//起始位置：寻找最后一个小于等于x的数，所以是不断往右逼近 
		l=0,r=n-1;
		while(l < r){
			int mid = l + r + 1>> 1;
			if(a[mid] <= x) l=mid; //往右边逼近 
			else r = mid - 1;
		} 
		
		cout << l << endl;
		 
	}
	
}

高精度

一般四种情况，len(A)<=10^6, a <= 10^9 ，大写字母是大数

A + B
A - B
A * a
A / a

基本思路：用数组来模拟加法过程；为了方便进位，个位在数组最左边。相当于把输入的第一位放到最后一位

一般只涉及大整数，浮点数

A+B

在这里插入图片描述

基本公式：Ci = Ai + Bi + t,t为进位

#include<iostream>
#include<vector>
#include<string>

using namespace std;

vector<int> A,B,C;
void add(vector<int> &A,vector<int> &B){
	
	int t = 0;
	//这里的代码简洁巧妙
	for(int i=0;i<A.size() || i<B.size();i++){
		if(i < A.size()) t+=A[i];
		if(i < B.size()) t+=B[i];
		
		C.push_back(t%10);
		t/=10;
		
	}
	if(t) C.push_back(t);
}
int main(){
	string a,b;
	cin >> a >> b;
	for(int i = a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
	for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
	
	add(A,B);

	for(int i=C.size()-1;i>=0;i--)  cout << C[i];
	
}

双指针

for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;

    // 具体问题的逻辑
}

注意：i在前面跑，j在后面追
常见问题分类：
(1) 对于一个序列，用两个指针维护一段区间
(2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

核心思想：在这里插入图片描述
双指针就是在朴素算法上利用一些单调性，使得本来需要枚举O(n^2)的变成O(n),

利用当前状态与以前状态有关，就可以去掉一些枚举

最长连续不重复子序列

小区间重复了，大区间一定会重复，所以随着i的变大，j不需要回退了，j要么增加要么不变
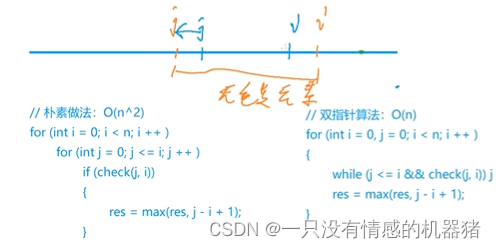
在这里插入图片描述

真的是诗一样的代码
如果数据量很大，就只能用哈希表来纪录

#include<iostream>
#include<set>
#include<algorithm>
using namespace  std;

const int N =1e5+10 ;
int a[N],cnt[N];
int n;

int main(){
	scanf("%d",&n);
	for(int i=0;i<n;i++){
		scanf("%d",&a[i]);
	}
	int ans=1;
	
	for(int i=0,j=0;i<n;i++){
		cnt[a[i]]++;
		while(cnt[a[i]]>1){
			
			cnt[a[j]]--;
			j++;
		} 
		ans = max(ans,i-j+1);
		
	}
	cout << ans;
	
}

判断子序列

统计子矩阵（二维）

https://www.acwing.com/activity/content/code/content/4139263/

对于二维的双指针问题，固定纵坐标，在横坐标上使用双指针即可

离散化

特指整数离散化，
应用情况：值域很大，但是数据量比较少，

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

typedef pair<int,int> PII;
const int N = 3e5+10;
int n,m;
vector<PII> add,query;
vector<int> alls;
int a[N],s[N];//a[i]对应的离散化后的值为i+1; 

// 将x离散化为find(x) 
int find(int x){
	int l=0,r=alls.size()-1;
	while(l<r){
		int mid = l + r >> 1;
		if(alls[mid]>=x) r=mid;
		else l = mid+1;
		
	}
	return l+1;//是前缀和，下标从1开始 
}
int main(){
	cin >> n >> m;
	for(int i=0;i<n;i++) {
		int x,c;
		cin >> x >> c;
		add.push_back({x,c}); 
		alls.push_back(x);
	} 
	for(int i=0;i<m;i++){
		int l,r;
		cin >> l >> r;
		query.push_back({l,r});
		alls.push_back(l);
		alls.push_back(r);
	}
	
	//去重
	sort(alls.begin(),alls.end());
	alls.erase(unique(alls.begin(),alls.end()),alls.end());
	
	//处理输入
	for(auto item:add){
		a[find(item.first)] += item.second;
	} 
	//处理前缀和
	for(int i=1;i<=alls.size();i++){//这里是all.size()
		s[i] = s[i-1] + a[i];
	} 
	
	//查询
	for(auto item:query){
		int l=find(item.first),r=find(item.second);
		cout << s[r] - s[l-1]<<endl;
	} 
	
}

java里没有去重函数，那么实现思路为：
双指针算法，把数组中满足①是第一个数②与前一个数不相同的数都提取出来
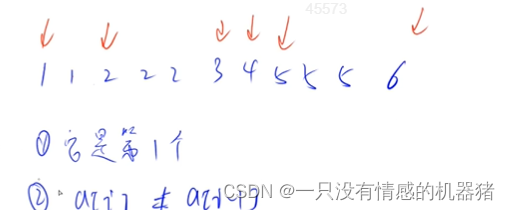
在这里插入图片描述
实现思路：

区间和

数据量比较少的情况下直接前缀和就行，这里数据量比较大就再加个离散化映射就行

前缀与差分

细节：1.统一下标从1开始，令A[0]=0

一维前缀和

构造:

S[i] = a[1] + a[2] + … a[i]
S[i] = S[i-1] + a[i]

性质
a[l] + … + a[r] = S[r] - S[l - 1]

#include<iostream>
using namespace std;

int n,m,l,r;
const int N =100010;
int a[N],s[N];

int main(){
    s[0]=0;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    
    for(int i=1;i<=n;i++) s[i] = s[i-1]+a[i];
    
    for(int i=0;i<m;i++){
     scanf("%d%d",&l,&r);
    printf("%d\n",s[r]-s[l-1]);
    }
    
}

二维前缀和

1.性质
[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
2. 例题
输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。

#include<iostream>
using namespace std;
const int N = 1010;
int n,m,q,x1,x2,y1,y2;
int A[N][N],S[N][N];

int main(){
    scanf("%d%d%d",&n,&m,&q);
    
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&A[i][j]);
        }
    }
    //构造前缀和矩阵
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            S[i][j] = S[i-1][j] + S[i][j-1] -S[i-1][j-1] + A[i][j];
        }
    }
    
    while(q--){
        cin>>x1>>y1>>x2>>y2;
        cout << S[x2][y2] - S[x2][y1-1] - S[x1-1][y2] + S[x1-1][y1-1] <<endl;//下标一定要小心 
    }
    return 0;
}

差分

原数组：a[1],a[2]…a[n]
递推公式：

b[1]=a[1],b[2]=a[2]-a[1]….b[n]=a[n]-a[n-1]
b[i] = a[i] - a[i-1]

差分数值不以递推公式构造，以下面模板代码构造

性质：

差分数组的前缀和就是原数组；
第b[l]+c等价于把a[l]以及之后的数全部加c（因为前缀和）；
给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c

模板代码：

	void insert(int l,int r,int c){
	B[l] += c;
	B[r+1] -= c;
}
	//构造差分数组B 
	insert(i,i,A[i]);

例题：
输入一个长度为 n 的整数序列。接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r]之间的每个数加上 c。请你输出进行完所有操作后的序列。
代码：

#include<iostream>
using namespace std;
const int N = 100010;
int n,m,l,r,c;
int A[N],B[N];
void insert(int l,int r,int c){
	B[l] += c;
	B[r+1] -= c;
}

int main(){
	cin >> n >> m;
	for(int i=1;i<=n;i++){
		scanf("%d",&A[i]);
		//构造差分数组B 
		insert(i,i,A[i]);
	}
	//进行操作 
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&l,&r,&c);
		insert(l,r,c);
	}
	
	//计算前缀和
	for(int i=1;i<=n;i++){
		B[i] += B[i-1];
		printf("%d ",B[i]);
	} 
}

二维差分

理解：https://www.acwing.com/solution/content/27325/
递推公式：
b[i][j] = a[i][j]-a[i-1][j]-a[i-1][j]+a[i-1][j-1]
即当前元素减去左边元素再减去上边元素再加上左上角元素

性质：

b(i,j) +c 等于(i,j)右下方全部元素都加上了C
给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：

S[x1, y1] += c, S[x2 + 1, y2 + 1] += c,
 S[x1, y2 + 1] -= c, S[x2 + 1, y1] -= c

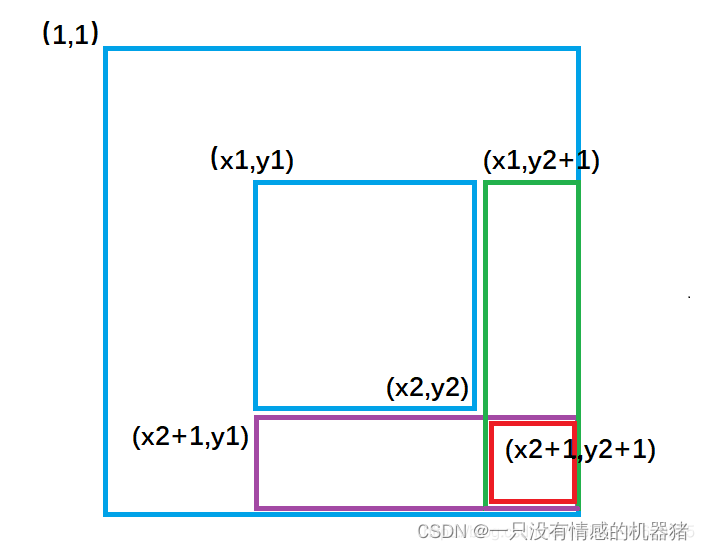
在这里插入图片描述

模板代码：

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}
insert(i, j, i, j, a[i][j]);      //构建差分数组

代码

#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}
int main()
{
    int n, m, q;
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            insert(i, j, i, j, a[i][j]);      //构建差分数组
        }
    }
    while (q--)
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];  //二维前缀和
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            printf("%d ", b[i][j]);
        }
        printf("\n");
    }
    return 0;
}

区间合并

基本思想——贪心
关键点：以左端点为依据，将所有区间排序
在这里插入图片描述
如果是第三种情况，就表明右边的区间和这个区间都没有关系了；

案例模拟：
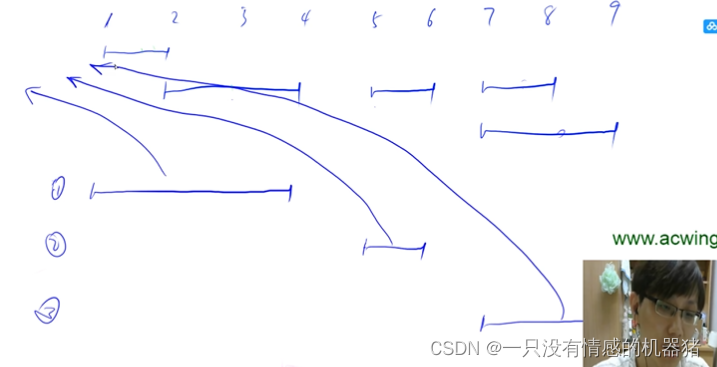
在这里插入图片描述

模板:

// 将所有存在交集的区间合并
void merge(vector<PII> &segs)
{
 vector<PII> res;
 sort(segs.begin(), segs.end());
 int st = -2e9, ed = -2e9;
 for (auto seg : segs)
 if (ed < seg.first)
 {
 if (st != -2e9) res.push_back({st, ed});
 st = seg.first, ed = seg.second;
 }
 else ed = max(ed, seg.second);
 if (st != -2e9) res.push_back({st, ed});
 segs = res;
}

关于排序在贪心中的重要性：https://www.acwing.com/solution/content/108899/

模板题代码

#include<iostream>
#include<vector>
#include <cstring>
#include <algorithm>

using namespace std;
typedef pair<int,int> PII;

int n;
vector<PII> segs,res; 

int merge(vector<PII> &segs){
	
	int st=-2e9,ed=-2e9;//初值使得一定不交叉 
	for(auto seg:segs){
		if(ed<seg.first)//不交叉了 
		{
			if(st!=-2e9)//如果不是初值，就可以入栈 
		    	res.push_back({st,ed}); 
			st = seg.first;
			ed = seg.second;
					
		}else{
			ed = max(ed,seg.second);//否则右边界取最右边的那个 
		}
	}
	//最后一个区间也要取出来 
	if(st!=-2e9)//如果不是初值，就可以入栈 
		res.push_back({st,ed}); 
	return res.size(); 
}
int main(){
	
	cin >> n;
	while(n--)
	{
		int l,r;
		cin>>l>>r;
		segs.push_back({l,r});
	}
	sort(segs.begin(),segs.end());//排序要记得
	cout << merge(segs);
}