淼淼刷力扣（特别篇区间DP1）

最新推荐文章于 2023-04-28 16:47:32 发布

三水还得练

最新推荐文章于 2023-04-28 16:47:32 发布

阅读量404

点赞数 4

分类专栏：力扣题解文章标签：动态规划算法 c++ 数据结构

本文链接：https://blog.youkuaiyun.com/qq_45678698/article/details/117585959

版权

力扣题解专栏收录该内容

114 篇文章

订阅专栏

本文介绍了区间动态规划在解决石子合并与基因合并问题上的应用，通过详细解析思路和代码实现，阐述了如何确定状态、初始化、建立状态转移方程及寻找答案。重点讲解了如何通过枚举区间断点找到最优合并策略，并提供了快速获取区间和的技巧。文章适合初学者理解区间DP，并提供了完整的C++代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

【努力刷力扣】第三十八天 --- 区间DP（洛谷P1880 [NOI1995] 石子合并+PTA-基因合并）

引言
题目要求：（二题本质一样）

引言

本人初次尝试写博客，希望各位看官大佬多多包容
有错误希望巨巨们提出来，我一定会及时改正，谢谢大家
在自己最好的年纪，找到了未来的目标
还有1年奋斗刷题，明年去面试实习，加油！
博主最近要参加竞赛，所以暂时调整训练计划。

题目要求：（二题本质一样）

1、PTA
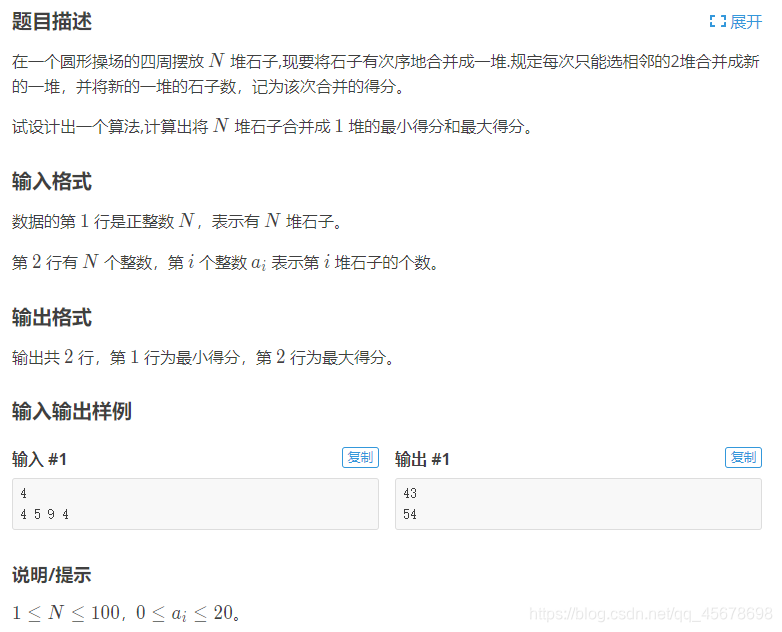
在这里插入图片描述
2、洛谷石子合并

前序知识

1、博主最近刚刚接触区间DP，只是套板子做题，有的的地方理解的并不深刻，所以读者老爷们如果觉得不清晰透彻请移步1、另一位博主的区间动态规划例题与解析2、OI Wiki-区间DP，以上两个网站内有较为详尽的区间DP解析。
2、无论我们在学校还是在课本上刚刚接触DP的时候，博主感觉很乱没有头绪，到处都是复杂的符号,经过大佬们给博主讲解之后，我认为（并不一定对，得根据特定题意走，有错误大家及时指出）区间DP就是四个过程：找好多少种状态，根据题意赋初始值，找状态转移方程，找寻答案，那么接下来我将从这四个方面为大家解析这两道题。

整体思路：因为最大最小思路一致，所以只说明最大情况

1、定状态：

我们就是要将几堆石子给合并成一堆，所以我们抽象成数学问题看，就是把一个区间的石子给合并，所以两个状态i,j，分别表示区间头和尾，所以用mx[i][j]表示该区间状态,其实博主最开始也被二维数组搞蒙了，其实不必看二维数组，就知道他表示了一个区间的状态即可。

2、赋初始值：

因为单独一堆石子是没有任何代价的，所以mx[i][i]=0。在计算mx[i][j]之前，要为其赋予0初始值，因为要算他的最大值。

3、状态转移方程：

这个真的是重中之重
在这里插入图片描述
我们这么理解，有这样一堆石子 3，5，8，7 合并他们的时候，3+5+7+8的数值是固定的，那么我们要这个区间内的最大值，怎么办，这就涉及了DP问题的另一方面，什么问题可以使用DP。一个问题可以使用DP，那么他就可以拆分成为若干个与之相同的子问题，在求解一个大区间最优的时候由他的子区间最优所得到。所以这个区间最大值就要看他的子区间，找到子区间怎么是最大的。

综上：我们只需要枚举区间断点，将区间分解成若干子状态，找到子区间中怎样合并能让状态值最大就行，最后一定别忘了我当前区间合并本身的消耗即可。

4、找答案：

当我们处理完1到n的区间，就意味着我们找到了最终状态，但是我们是个环，就得把环上所有的肯能长度为n，且断点不同的所有区间情况考虑周全。

具体代码（内附注释）

注：特定技巧
1、快速获得某个区间的和算法：前缀和算法，时间复杂度O(1)，获得i到j的区间和时，用a[j]-a[i-1]即可
2、因为我所有的石子是一个环形排列，所以一定不能只考虑1到n这个范围，这样的话你就没有按照环形去设计，那么我们采用一个技巧，就是把1到n-1的项再抄一遍即可
在这里插入图片描述
通过上图可知，我们只需要在后面抄n-1个即可，但事实上我们抄了n个,所以下方双层循环处外层循环初始值是2，来略过最后一个多抄的那个数。
（其实在后面抄几遍都行，看具体要求）

#include <iostream>
#include <algorithm>
using namespace std;
int mx[404][404];//最大值状态
int mn[404][404];//最小值状态
int a[404] = { 0 };//存石子的数组

int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		a[i + n] = a[i];//在后面抄一遍，构造环
	}
	for (int i = 1; i <= 2 * n; i++) {
		a[i] += a[i - 1];//构造前缀和
		mx[i][i] = 0;//初始化
		mn[i][i] = 0;//初始化
	}
	for (int l = 2; l <= n; l++) {//开始状态转移，初始值是为了略过最后面多抄的数
		for (int i = 1, j; i + l <= 2 * n; i++) {
			j = i + l - 1;//区间右端点
			mx[i][j] = 0;
			mn[i][j] = 1 << 30;//初始化
			for (int k = i; k < j; k++) {//状态转移方程
				mx[i][j] = max(mx[i][j], mx[i][k] + mx[k + 1][j]);
				mn[i][j] = min(mn[i][j], mn[i][k] + mn[k + 1][j]);
			}
			mx[i][j] += a[j] - a[i - 1];//加上本次的代价
			mn[i][j] += a[j] - a[i - 1];
		}
	}
	int ans_min = 1 << 30;//初始化结果
	int ans_max = 0;
	for (int i = 1; i <= n; i++) {//在环上长度为n的区间，通过不同断点找答案
		ans_max = max(ans_max, mx[i][i + n - 1]);
		ans_min = min(ans_min, mn[i][i + n - 1]);
	}
	cout << ans_min << endl << ans_max;//洛谷输出
	cout << endl;
	cout << ans_min << ' ' << ans_max;//PTA输出
}