第三节课：

---

题目一

首先要保证能整除。如果只考虑i洗衣机，左右两个分别看成一个整体。正数表示需要扔出衣服，负数表示需要衣服：1 两边都为负，i需要扔出两边绝对值之和的衣服，也就是需要绝对值之和轮（至少）；2 两边都为正，i需要两边的最大值轮（至少）；3 左负右正，i需要两边绝对值的最大值轮（至少）。

将每个位置的最少轮数求出，其中最痛的瓶颈达成，其他的瓶颈也就达成了，即最大的轮数就是答案。

代码实现：

int f(vector<int>& arr) {
	if (arr.size() < 2) {
		return 0;
	}
	int sum = 0;
	for (int i = 0; i < arr.size(); i++) {
		sum += arr[i];
	}
	if (sum % arr.size() != 0) {
		return -1;//无效值
	}
	int avg = sum / arr.size();
	int leftSum = 0;
	int res = 0;
	for (int i = 0; i < arr.size(); i++) {
		int leftRest = leftSum - i * avg;//正表示需要扔出衣服；负表示需要输入衣服
		int rightRest = sum - leftSum - arr[i] - (arr.size() - 1 - i) * avg;
		if (leftRest < 0 && rightRest < 0) {
			res = max(res, abs(leftRest) + abs(rightRest));
		}
		else {
			res = max(res, max(abs(leftRest), abs(rightRest)));
		}
		leftSum += arr[i];
	}
	return res;
}

---

题目二

二维数组调整的一个方法论：不要关注局部位置怎么变，要设计宏观调度。

代码实现：

void printEdge(vector<vector<int>>& arr, int x, int y, int i, int j) {
	if (x == i) {
		for (int k = y; k <= j; k++) {
			cout << arr[i][k] << " ";
		}
		cout << endl;
	}
	else if (y == j) {
		for (int k = x; k <= i; k++) {
			cout << arr[k][j] << " ";
		}
		cout << endl;
	}
	else {
		int k = y;
		while (k <= j) {
			cout << arr[x][k] << " ";
			k++;
		}
		k = x + 1;
		while (k <= i) {
			cout << arr[k][j] << " ";
			k++;
		}
		k = j - 1;
		while (k >= y) {
			cout << arr[i][k] << " ";
			k--;
		}
		k = i - 1;
		while (k >= x + 1) {
			cout << arr[k][y] << " ";
			k--;
		}
		cout << endl;
	}
		
}

void printMatrix(vector<vector<int>>& arr) {
	int x = 0;
	int y = 0;
	int i = arr.size() - 1;
	int j = arr[0].size() - 1;

	while (x <= i && y <= j) {
		printEdge(arr, x, y, i, j);
		x++;
		y++;
		i--;
		j--;
	}

}

---

题目三

每个框自己变，定义一个框上的元素怎么变的元素，还是左上角点往右下角走、右下角点往左上角走。每一个框分边长减一组

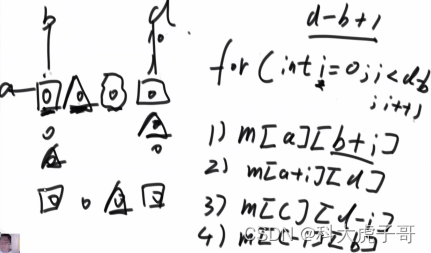
代码实现：

void rotateEdge(vector<vector<int>>& arr, int x, int y, int i, int j) {
	for (int k = 0; k < i - x; k++) {
		int temp = arr[x][y + k];
		arr[x][y + k] = arr[i - k][y];
		arr[i - k][y] = arr[i][j - k];
		arr[i][j - k] = arr[x + k][j];
		arr[x + k][j] = temp;
	}
}

void rotate(vector<vector<int>>& arr) {
	int x = 0;
	int y = 0;
	int i = arr.size() - 1;
	int j = arr[0].size() - 1;

	while (x < i) {
		rotateEdge(arr, x, y, i, j);
		x++;
		y++;
		i--;
		j--;
	}
}

---

题目四

两个点A、B初始时在左上角，A每次向右移动，B每次向下移动，打印以A和B为端点对角线，打印顺序交替进行；当A到达右边界，则改为向下移动，当B到达下边界，则改为向右移动；直到A，B达到右下角。

代码实现：

void printLevel(vector<vector<int>>& arr, int ar, int ac, int br, int bc, bool flag) {
	int i = 0;
	int j = 0;
	if (flag) {//从上往下
		i = ar;
		j = ac;
		while (i <= br) {
			cout << arr[i][j] << " ";
			i++;
			j--;
		}
	}
	else {//从下往上
		i = br;
		j = bc;
		while (i >= ar) {
			cout << arr[i][j] << " ";
			i--;
			j++;
		}
	}
}

void zigzag(vector<vector<int>>& arr) {
	int ar = 0;
	int ac = 0;
	int br = 0;
	int bc = 0;
	int M = arr.size();
	int N = arr[0].size();
	bool flag = false;//从下往上
	while (ar != M) {
		printLevel(arr, ar, ac, br, bc, flag);
		ar = ac == N - 1 ? ar + 1 : ar;
		ac = ac == N - 1 ? ac : ac + 1;

		bc = br == M - 1 ? bc + 1 : bc;
		br = br == M - 1 ? br : br + 1;
		flag = !flag;
	}
}

---

题目五

如果让拼的长度n是质数时，只使用操作二的步骤数就是最小的步骤数n-1（不是说调一操作，只是调一操作的总步骤数不会好于只调操作二的总步骤数）。
如果让拼的长度n不是质数，那么可以将它分解成几个质数的乘积。首先拼成质数个a，然后再将质数个a翻质数倍，依次类推。

bool isPrim(int n) {
	for (int i = 2; i < n; i++) {
		if (n % i == 0) {
			return false;
		}
	}
	return true;
}

vector<int> getDivsSumAndCount(int n) {
	vector<int>res(2);
	for (int i = 2; i <= n; i++) {
		while (n % i == 0) {
			n = n / i;
			res[0] += i;
			res[1]++;
		}
	}
	return res;
}

int minOps(int n) {
	if (n < 2) {
		return 0;
	}
	if (isPrim(n)) {
		return n - 1;
	}
	vector<int>arr = getDivsSumAndCount(n);
	return arr[0] - arr[1];
}

---

题目六

方法一：建立词频表，加入大根堆，大根堆用词频排序，弹出前k个
方法二：建立词频表，用小根堆，大小限制不能超过k，表示目前出现最多的两个用小根堆组织，堆顶相当于是门槛。比方法一节省空间

代码实现：

//方法一
class Cmp01 {
public:
	bool operator()(const pair<string, int>& a, const pair<string, int>& b) {
		return a.second < b.second;
	}
};

vector<string> maxTimesK01(vector<string>& strs, int K) {
	unordered_map<string, int>mp;
	for (string s : strs) {
		if (mp.find(s) == mp.end()) {
			mp.insert({ s,1 });
		}
		else {
			mp[s]++;
		}
	}
	priority_queue<pair<string, int>, vector<pair<string, int>>, Cmp01>p;
	for (pair<string, int> m : mp) {
		p.push(m);
	}
	vector<string>res;
	for (int i = 0; i < K; i++) {
		res.push_back(p.top().first);
		p.pop();
	}
	return res;
}

//方法二
class Cmp02 {
public:
	bool operator()(const pair<string, int>& a, const pair<string, int>& b) {
		return a.second > b.second;
	}
};
vector<string> maxTimesK02(vector<string>& strs, int K) {
	unordered_map<string, int>mp;
	for (string s : strs) {
		if (mp.find(s) == mp.end()) {
			mp.insert({ s,1 });
		}
		else {
			mp[s]++;
		}
	}
	priority_queue<pair<string, int>, vector<pair<string, int>>, Cmp02>p;
	for (pair<string, int> m : mp) {
		if (p.size() < K || m.second > p.top().second) {
			if (p.size() < K) {
				p.push(m);
			}
			else {
				p.pop();
				p.push(m);
			}
		}
	}
	vector<string>res;
	while (!p.empty()) {
		res.push_back(p.top().first);
		p.pop();
	}
	return res;
}

---

题目七

实现一种结构：随时接收用户的字符串，并随时输出字符串种出现频率最高的前K个。
因为字符串是动态变化的，如果再按照题目六的方法做，每次都要重新调用函数计算，代价很大。需要用一个动态结构维持出现频率前K个的字符，更新的代价不能太大–>改写堆！
需要一个词频表、堆、堆位置map：记录某一字符串在堆上的位置

不能使用系统提供的堆，因为系统提供的堆就像是一个黑盒，只支持加入 弹出操作，而不能对其中的数据进行修改，然后再调成堆。
代码实现：

class Ticket {
public:
	int heapSize;
	vector<string>heap;//堆
	unordered_map<string, int>strMap;//词频表
	unordered_map<string, int>strIndexMap;//str在堆上的位置

	Ticket(int K) {//统计top K
		this->heapSize = 0;
		heap.resize(K);
	}

	void add(string str) {
		if (strMap.find(str) == strMap.end()) {//之前没有加入过
			strMap.insert({ str,1 });
			if (heapSize < heap.size()) {//堆不满，直接加
				heapInsert(str);
			}
			else {//堆满了，当前又是第一次出现，不可能超过门槛
				strIndexMap.insert({ str,-1 });
			}
		}
		else {//之前出现过
			strMap[str]++;//词频加一
			if (strIndexMap[str] == -1) {//当前不在堆上
				if (strMap[str] > strMap[heap[0]]) {//干过了堆头，可以入堆
					heap[0] = str;
					strIndexMap[str] = 0;
					heapfy(0);
				}
			}
			else {//之前在堆上
				heapfy(strIndexMap[str]);
			}
		}
	}

	void printTopK() {
		for (int i = 0; i < heapSize; i++) {
			cout << heap[i] << " ";
		}
		cout << endl;
	}
private:
	void swap(int i, int j) {
		strIndexMap[heap[i]] = j;
		strIndexMap[heap[j]] = i;
		string temp = heap[i];
		heap[i] = heap[j];
		heap[j] = temp;
	}
	void heapInsert(string str) {
		heap[heapSize] = str;
		heapSize++;
		int i = heapSize - 1;
		while (strMap[heap[i]] < strMap[heap[(i - 1) / 2]]) {
			swap(i, (i - 1) / 2);
			i = (i - 1) / 2;
		}
	}

	void heapfy(int i) {
		int left = 2 * i + 1;//左孩子下标
		while (left < heapSize) {
			int smallest = (left + 1 < heapSize) && (strMap[heap[left + 1]] < strMap[heap[left]]) ? left + 1 : left;
			if (strMap[heap[i]] > strMap[heap[smallest]]) {
				swap(i, smallest);
				i = smallest;
				left = 2 * i + 1;
			}
			else {
				break;
			}
		}
	}
};