题目一

方法一:将数组放入哈希表中;遍历哈希表,每遍历到一个数,在哈希表中查询比他大k的数在不在哈希表中
代码实现:
//方法一
vector<vector<int>> subValueEqualK01(vector<int>& arr, int k) {
set<int>s;
vector<vector<int>>res;
for (int i = 0; i < arr.size(); i++) {
s.insert(arr[i]);
}
//for (set<int>::iterator it = s.begin(); it != s.end(); it++) {
// if (s.find(*it + k) != s.end()) {
// res.push_back(vector<int>({ *it,*it + k }));
// }
//}
for (int a : s) {
if (s.find(a + k) != s.end()) {
res.push_back(vector<int>({ a,a + k }));
}
}
return res;
}
方法二:对数组进行排序;使用双指针l和r;首先让l和r都指向0位置;r有移动,比较l、r对应位置的差值,如果等于k–>l、r都向右移动,如果小于k–>r向右移动,如果大于k–>l向右移动;直到r在最右侧,并且当前l位置与r位置的差值小于k
代码实现:
//方法二
vector<vector<int>> subValueEqualK02(vector<int>& arr, int k) {
vector<vector<int>>res;
sort(arr.begin(), arr.end());
int l = 0;
int r = 0;
while (r < arr.size() && l < arr.size()) {
if (arr[r] - arr[l] == k) {
res.push_back(vector<int>({ arr[l],arr[r] }));
while (r < arr.size() && arr[r] - arr[l] == k) {
r++;
}
}
else if (arr[r] - arr[l] < k) {
r++;
}
else {
l++;
}
}
return res;
}
题目二

题目大致可以分为,以业务为主的题(笔试:55%;面试:30%):求解完全在于分析这个问题本身,虽然也会用一些技巧加速;以技巧为主的题(笔试45%;面试:70%):主要考察某一技巧/原型会不会,会的话,用一下就解决了。
本题是以以业务为主的题。分类讨论:1) 平均值相同
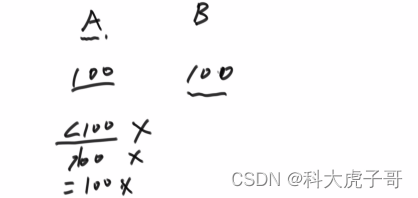
2) 平均值不同:只可能将大平均值的集合的数放入小平均值的集合,优先拿符合条件最小的数

代码实现:
//本题注意coding的技巧
int getSum(vector<int>& arr) {
int sum = 0;
for (int i = 0; i < arr.size(); i++) {
sum += arr[i];
}
return sum;
}
double getAver(double sum, int size) {
return sum / size;
}
int f(vector<int>& a, vector<int>& b) {
double sumOfA = getSum(a);
double sumOfB = getSum(b);
if (getAver(sumOfA, a.size()) == getAver(sumOfB, b.size())) {
return 0;
}
if (getAver(sumOfA, a.size()) < getAver(sumOfB, b.size())) {
int sumOfT = sumOfA;
sumOfA = sumOfB;
sumOfB = sumOfT;
vector<int>tempArr = a;
a = b;
b = tempArr;
}
sort(a.begin(), a.end());
set<int>s;
for (int num : b) {
s.insert(num);
}
int sizeOfA = a.size();
int sizeOfB = b.size();
int res = 0;
for (int i = 0; i < a.size(); i++) {
double cur = a[i];
if (cur<getAver(sumOfA, sizeOfA) && cur>getAver(sumOfB, sizeOfB) && s.find(cur) == s.end()) {
sumOfA -= cur;
sizeOfA--;
sumOfB += cur;
sizeOfB++;
s.insert(cur);
res++;
}
}
return res;
}
题目三

借用上节课的思路:用一个变量count,遇到‘(’count++,遇到‘)’count–,count所能达到的最大值就是这题的解
代码实现:
int depth(string& s) {
int count = 0;
int res = 0;
for (int i = 0; i < s.length(); i++) {
if (s[i] == '(') {
count++;
}
else {
res = max(res, count);
count--;
}
}
return res;
}
题目四
给定一个由左括号和右括号组成的字符串,请找到最长的有效括号子串(连续)
看到子序列/子串/子数组的题目(连续):就求以每个位置结尾的情况下答案是多少,最优答案一定在其中。
动态规划:以左括号结尾不可能有效。假设当前位置i是右括号,求dp[i],看dp[i-1]之前的一个字符是否位左括号,1) 如果是左括号,这dp[i]的值至少为dp[i-1]+2,2) 否则为0.


对于1) 如果是左括号,这dp[i]的值至少为dp[i-1]+2,因为在这个左括号之前可能会再接一个有效的字符串,但在这个有效的字符串之前不可能再接一个有效的字符串了,这个有效字符串已经把之前能接的全部接上了

代码实现:
int f(string& s) {
if (s.length() < 2) {
return 0;
}
vector<int>dp(s.length());
int pre = 0;
int res = 0;
for (int i = 1; i < s.length(); i++) {
if (s[i] == '(') {
dp[i] = 0;
}
else {
pre = i - 1 - dp[i - 1];
if (pre >= 0) {
if (s[pre] == ')') {
dp[i] = 0;
}
else {
dp[i] = dp[i - 1] + 2 + (pre - 1 >= 0 ? dp[pre - 1] : 0);
}
}
}
res = max(res, dp[i]);
}
return res;
}
题目五

假设原始栈为A,辅助栈为B。想让栈中元素升序排列,则需要在辅助栈中降序排列。从A栈中弹出元素,用一个辅助变量temp存储,如果符合辅助栈的排序规则,则直接压入栈中;否则将栈B中的元素不断弹出并压入栈A中,直到temp可以进入栈B;重复上述操作,直到栈A为空;最后再将栈B中的元素压回栈A。

代码实现:
void f(stack<int>& a) {
stack<int>b;
while (!a.empty()) {
int temp = a.top();
a.pop();
if (b.empty()) {
b.push(temp);
}
else {
while (!b.empty()&&temp > b.top()) {
a.push(b.top());
b.pop();
}
b.push(temp);
}
}
while (!b.empty()) {
a.push(b.top());
b.pop();
}
}
题目六

从左往右的尝试模型:i位置及之后有多少转化方法,所求即为f(0)。怎么做决定?1) s[0]==0,则返回0;2) s[i]!=0,则f(i+1)总有效;3) [i][i+1]<=26,则f(i+2)

代码实现:
//暴力递归
int p(string& s, int i) {//s[i..]有多少种转法
if (i == s.length()) {
return 1;
}
if (i > s.length()) {
return 0;
}
if ((s[i]) == '0') {
return 0;
}
int res = 0;
if (s[i] == '1') {
res = p(s, i + 1) + p(s, i + 2);
}
else if (s[i] == '2') {
res = p(s, i + 1);
if (i + 1 < s.length() && s[i + 1] <= '6') {
res += p(s, i + 2);
}
}
else {
res = p(s, i + 1);
}
return res;
}
int f(string& s) {
return p(s, 0);
}
//改动态规划
int f2(string& s) {
vector<int>dp(s.length() + 1);
dp[s.length()] = 1;
dp[s.length() - 1] = s[s.length() - 1] == '0' ? 0 : 1;
for (int i = s.length() - 2; i >= 0; i--) {
if (s[i] == '0') {
dp[i] = 0;
}
else if (s[i] == '1') {
dp[i] = dp[i + 1] + dp[i + 2];
}
else if (s[i] == '2') {
dp[i] = dp[i + 1];
if (s[i + 1] <= '6') {
dp[i] += dp[i + 2];
}
}
else {
dp[i] = dp[i + 1];
}
}
return dp[0];
}
题目七

方法一:先序遍历
代码实现:
class Node {
public:
int val;
Node* left;
Node* right;
Node(int val) {
this->val = val;
this->left = nullptr;
this->right = nullptr;
}
};
//方法一:先序遍历
//sum:从根节点到当前节点的路径和
void process(Node* head, int& res, int sum) {
if (head->left == nullptr && head->right == nullptr) {
res = max(res, sum + head->val);
return;
}
sum += head->val;
if (head->left != nullptr) {
process(head->left, res, sum);
}
if (head->right != nullptr) {
process(head->right, res, sum);
}
}
int maxWeight(Node* head) {
if (head == nullptr) {
return 0;
}
int res = INT_MIN;
process(head, res, 0);
return res;
}
方法二:二叉树的递归套路
代码实现:
//方法二:套路解
//返回以当前节点为头的最大路径和
int process02(Node* head) {
if (head->left == nullptr && head->right == nullptr) {
return head->val;
}
int next = INT_MIN;
if (head->left != nullptr) {
next = process02(head->left);
}
if (head->right != nullptr) {
next = max(next, process02(head->right));
}
return next + head->val;
}
题目八

有点二分的思想:根据题意,左上角最小,右下角最大,从偏向中间值的右上角开始找,如果当前值比aim大–>aim不可能在当前位置所在行的左边,所以当前位置向下移动;如果当前值比aim小–>aim不可能在当前位置所在列的下边,当前位置向左移动;直到达到左边界或者下边界。时间复杂度:O(M+N)。

bool f(vector<vector<int>>& arr, int aim) {
if (arr.size() == 0 || arr[0].size() == 0) {
return false;
}
int M = arr.size();
int N = arr[0].size();
int i = 0;
int j = N - 1;
while (i < M && j >= 0) {
if (arr[i][j] == aim) {
return true;
}
if (arr[i][j] < aim) {
i++;
}
else {
j--;
}
}
return false;
}
题目九
给定一个只包含0和1的矩阵,如果一行即存在0,又存在1,则所有的1在0的右边,返回1数量最多的行。
也是从右上角开始,如果左边有1,则一直向左;不能向左时,向下

vector<int> f(vector<vector<int>>& arr) {
if (arr.size() == 0 || arr[0].size() == 0) {
return vector<int>(1, -1);
}
int M = arr.size();
int N = arr[0].size();
int i = 0;
int j = N - 1;
vector<int>res;
int cur = 0;//当前找到的最大连续1
while (i < M && j >= 0) {
if (j == 0) {
if (arr[i][j] == 1) {
res.push_back(i);
}
i++;
}
else if (arr[i][j] == 1 && arr[i][j - 1] == 1) {
j--;
}
else {
if (arr[i][j] == 1 && arr[i][j - 1] != 1) {
if (res.size() == 0 || N - j >= cur) {
if (N - j > cur) {
res.clear();
cur = N - j;
}
res.push_back(i);
}
}
i++;
}
}
return res;
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








