HJ16 购物单--01背包问题

原创已于 2025-11-11 18:30:48 修改 · 984 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2025-11-11 17:50:00 首次发布

Leetcode-java 专栏收录该内容

80 篇文章

订阅专栏

购物单_牛客题霸_牛客网

描述

王强决定把年终奖用于购物，他把想买的物品分为两类：主件与附件。
∙ ∙主件可以没有附件，至多有 2 个附件。附件不再有从属于自己的附件。
∙ ∙若要购买某附件，必须先购买该附件所属的主件，且每件物品只能购买一次。
王强查到了 m件物品的价格，而他只有 n 元的预算。为了先购买重要的物品，他给每件物品规定了一个重要度，用整数 1∼5 表示。他希望在不超过预算的前提下，使满意度最大。

满意度定义为所购每件物品价格与重要度乘积之和。具体地说，记第 ii 件物品的价格为 vi，重要度为 wi；若共选中 k 件物品，编号为 j1,j2,…,jk则满意度计算为：

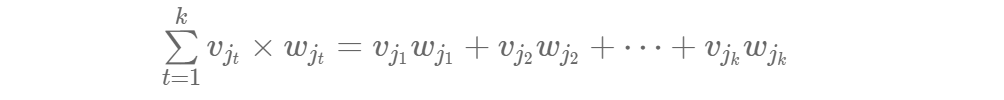
输入描述：

第一行输入两个整数 n,m代表预算、查询到的物品总数。

此后 mm 行，第 ii 行输入三个整数 vi,wi,qi
代表第 i 件物品的价格、重要度、主件编号。特别地qi=0 代表该物品为主件，否则表示该附件从属于主件 qi。编号即输入顺序，从 1 开始。

特别地，保证全部物品的价格 vv 均为 10的倍数；且每个主件的附件数不超过 2 个。

输出描述：

在一行上输出一个整数，代表王强可获得的最大满意度。

示例1

输入：

50 5
20 3 5
20 3 5
10 3 0
10 2 0
10 1 0
输出：
130
说明：
在这个样例中，第三、四、五件物品为主件，第一、二件物品为第五件物品的附件。这就意味着，如果购买了第一件物品或第二件物品，则必须购买第五件物品；但是特别地，如果同时购买了第一件物品和第二件物品，则只需要购买一次第五件物品。
我们可以证明，购买一、二、五件商品，获得的满意度最大，为 20×3+20×3+10×1=13020×3+20×3+10×1=130。

示例2

输入：

1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0
输出：

2200

代码思路：

问题背景

你有总预算 money，要购买若干物品。
物品分两类：
- 主件：q = 0
- 附件：q > 0，表示它是第 q 号物品的附件（q 一定是主件）
约束：
- 附件不能单独购买，必须和其主件一起买。
- 每个主件最多有 2 个附件。
目标：在不超过预算的前提下，最大化满意度总和（满意度 = 价格 × 重要度）。

解题策略：分组背包 + 枚举组合

- 预处理物品关系
  - 先读入所有物品。
  - 遍历一遍，把每个附件挂到对应主件的 a1 / a2 字段下。
- 为主件预计算 4 种购买方案 对每个主件 i，计算以下四种组合的总价格和总满意度：
  - 方案0：只买主件 → (v, satisfid)
  - 方案1：主件 + 附件1 → (v1, satisfid1)
  - 方案2：主件 + 附件2 → (v2, satisfid2)
  - 方案3：主件 + 附件1 + 附件2 → (v3, satisfid3)
- 动态规划（0-1 背包变种）
  - 状态定义：dp[i][j] 表示前 i 个物品中，花费不超过 j 的最大满意度。
  - 转移逻辑：
    - 如果是附件：不能单独选 → dp[i][j] = dp[i-1][j]
    - 如果是主件：枚举上述 4 种合法组合（若价格 ≤ j），取最大值。
- 输出结果：dp[n][money]

代码实现

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int money =in.nextInt();
        int n =in.nextInt();
        if(n<=0||money<=0){
            System.out.println(0);
        }
        good[] gs = new good[n+1];
        for(int i=1;i<=n;i++){
            int v= in.nextInt();//价格、
            int p= in.nextInt();//重要度、
            int q= in.nextInt();//主件编号
            gs[i] = new good(v*p,v,q);
        }
        for(int i =1;i<=n;i++){
            int q = gs[i].q;
            if(q>0){
                if(gs[q].a1==0){
                    gs[q].setA1(i);
                }else{
                    gs[q].setA2(i);
                }
            }
        }
        
        for(int i=1;i<=n;i++){
            int v=0,v1=0,v2=0,v3=0;
            int satisfid=0,satisfid1=0,atisfid2=0,atisfid3=0;
            satisfid = gs[i].satisfid;
            v=gs[i].v;
            if(gs[i].a1!=0){
                gs[i].setSatisfid1(satisfid+gs[gs[i].a1].satisfid);
                gs[i].setV1(v+gs[gs[i].a1].v);
            }
            if(gs[i].a2!=0){
                gs[i].setSatisfid2( satisfid+gs[gs[i].a2].satisfid);
                gs[i].setV2(v+gs[gs[i].a2].v);
            }
            if(gs[i].a1!=0 && gs[i].a2!=0){
                gs[i].setSatisfid3(satisfid+gs[gs[i].a1].satisfid+gs[gs[i].a2].satisfid);
               gs[i].setV3(v+gs[gs[i].a1].v+gs[gs[i].a2].v);
            }
        }

        int[][] dp = new int[n+1][money+1];
        for(int i = 1;i<=n;i++){

            for(int j=1;j<=money;j++){
                if(gs[i].q>0){
                    dp[i][j] = dp[i-1][j];
                }else{
                    dp[i][j] = dp[i-1][j];
                    if(gs[i].v<=j){
                        dp[i][j] =Math.max(dp[i][j],dp[i-1][j-gs[i].v]+gs[i].satisfid);
                    }
                    if(gs[i].v1<=j&&gs[i].v1>0){
                        dp[i][j] =Math.max(dp[i][j],dp[i-1][j-gs[i].v1]+gs[i].satisfid1);
                    }
                    if(gs[i].v2<=j&&gs[i].v2>0){
                        dp[i][j] =Math.max(dp[i][j],dp[i-1][j-gs[i].v2]+gs[i].satisfid2);
                    }
                    if(gs[i].v3<=j&&gs[i].v3>0){
                        dp[i][j] =Math.max(dp[i][j],dp[i-1][j-gs[i].v3]+gs[i].satisfid3);
                    }
                    
                }
            }
        }
        System.out.println(dp[n][money]);
       
    }
}

class good{
   int satisfid ;
   int v;
   int q;

   int a1 = 0;
   int a2 = 0;

   int v1=0;
   int v2=0;
   int v3=0;

   int satisfid1=0;
   int satisfid2=0;
   int satisfid3=0;

   public good(int satisfid,int v,int q){
    this.satisfid = satisfid;
    this.v = v;
    this.q = q;
   }

   public void setA1(int x){
    this.a1 = x;
   }

   public void setA2(int x){
    this.a2 = x;
   }
   public void setV1(int x){
    this.v1 = x;
   }
   public void setV2(int x){
    this.v2 = x;
   }
   public void setV3(int x){
    this.v3 = x;
   }
   public void setSatisfid1(int x){
    this.satisfid1 = x;
   }
   public void setSatisfid2(int x){
    this.satisfid2 = x;
   }
   public void setSatisfid3(int x){
    this.satisfid3 = x;
   }
}