深度学习线性代数回顾

深度学习中线性代数回顾

一、范数

在机器学习中，我们使用称为**范数（norm）**的函数来衡量向量的大小。

1. $L^p$ 范数

$L^p$ 范数定义如下：

$$||\mathbf{x}|{|}_p=(\sum _i|x_i{|}^p{)}^{\frac{1}{p}}$$
其中， $p\in \mathbb{R},p\ge 1$
范数（包括 $L^p$ 范数）是将向量映射到非负值的函数，向量 $\vec{x}$ 的范数衡量从原点到点 $\vec{x}$ 的距离，有如下性质：

• $f(\vec{x})=0\Rightarrow \vec{x}=0$
• $f(\vec{x}+\vec{y})\le f(\vec{x})+f(\vec{y})$ （triangle inequality）
• $\forall \alpha \in \mathbb{R},f(\alpha \vec{x})=|\alpha |f(\vec{x})$

2. $L^2$ 范数（Euclidean norm）

$L^2$ 可以简单用 ${\mathbf{x}}^T\mathbf{x}$ 计算。

3. $L^1$ 范数

$L^2$ 范数在原点附近增长十分缓慢，某些机器学习情况下，需要区分恰好是0的元素和非零但值很小的元素非常重要，于是，我们使用在各个位置斜率相同，
并且保持简单数学形式的函数： $L^1$ 范数，每当 $\mathbf{x}$ 中某个元素从0增加 $ϵ$ ，对应的 $L^1$ 范数也增加 $ϵ$

$$||\mathbf{x}|{|}_1=\sum _i|x_i|$$

4. $L^{\infty }$ 范数

也被称为最大范数，表示向量中具有最大幅值的元素的绝对值：

$$||\mathbf{x}|{|}_{\infty }=\underset{i}{\max }|x_i|$$

5. $Frobenius$ 范数

$$||\mathbf{A}|{|}_F=\sqrt{\sum _{i,j}{\mathbf{A}}_{i,j}^2}$$
用于衡量矩阵的大小，类似与向量的 $L^2$ 范数

---

二、矩阵分解

1.特征分解

关于特征分解的概念、计算以及相关性质不在此赘述，仅作补充
每个实对称矩阵都可以分解成特征向量和实特征值： $\mathbf{A}=\mathbf{Q}\Lambda {\mathbf{Q}}^T$
其中 $\mathbf{Q}$ 是 $\mathbf{A}$ 的特征值组成的正交矩阵，$\Lambda$ 是对角矩阵。特征值 ${\Lambda }_{i,j}$ 对应的特征向量是矩阵 $\mathbf{Q}$ 的第 $i$ 列，记作 ${\mathbf{Q}}_{:,i}$

特征向量和特征值的作用效果如下图所示

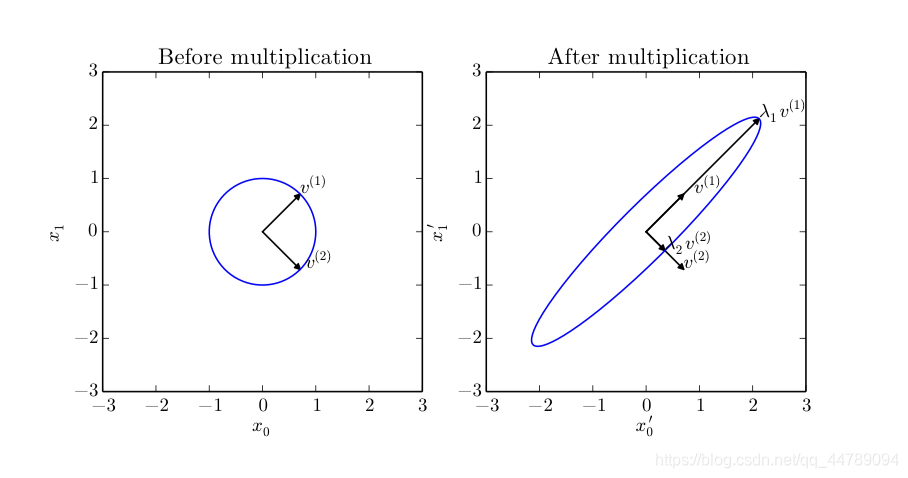
这里矩阵 $\mathbf{A}$ 有两个标准正交的特征向量，对应特征值为 ${\lambda }_1$ 的 ${\nu }^{(1)}$ 以及对应特征值为 ${\lambda }_2$ 的 ${\nu }^{(2)}$
左侧是所有单位向量 $\mu \in {\mathbb{R}}^2$ 的集合；右侧是所有 $\mathbf{A}\mu$ 点的集合，通过观察 $\mathbf{A}$ 拉伸单位圆的方式，我们看到它将 ${\nu }^{(i)}$ 方向的空间拉伸了 ${\lambda }_i$ 倍

注：

• 所有特征值都是正数的矩阵称为正定（positive definite）
• 所有特征值都是非负数的矩阵称为半正定（positive semidefinite）
• 所有特征值都是负数的矩阵称为负定（negative definite）
• 所有特征值都是非正数的矩阵称为半负定（negative semidefinite）

2.奇异值分解（SVD）

每个实数矩阵都有一个奇异值分解，但不一定都有特征分解，如非方阵

$$\mathbf{A}=\mathbf{U}\mathbf{D}{\mathbf{V}}^T$$
假设 $\mathbf{A}$ 是一个 $m\times n$ 的矩阵，那么 $\mathbf{U}$ 是一个 $m\times m$ 的矩阵， $\mathbf{D}$ 是一个 $m\times n$ 的矩阵， $\mathbf{V}$ 是一个 $n\times n$ 的矩阵

• 矩阵 $\mathbf{U}$ 和 $\mathbf{V}$ 都定义为正交矩阵，而矩阵 $\mathbf{D}$ 定义为对角矩阵， $\mathbf{D}$ 不一定为方阵
• 对角矩阵 $\mathbf{D}$ 对角线上的元素称为 $\mathbf{A}$ 的奇异值（singular value），矩阵 $\mathbf{U}$ 的列向量称为左奇异向量（left singular vector），矩阵 $\mathbf{V}$ 的列向量称为右奇异向量（right singular vector）
• 矩阵 $\mathbf{A}$ 的左奇异向量是 $\mathbf{A}{\mathbf{A}}^T$ 的特征向量， $\mathbf{A}$ 的右奇异向量是 ${\mathbf{A}}^T\mathbf{A}$ 的特征向量
• $\mathbf{A}$ 的非零奇异值是 ${\mathbf{A}}^T\mathbf{A}$ 特征值的平方根，同时也是 $\mathbf{A}{\mathbf{A}}^T$ 特征值的平方根

---

三、Moore-Penrose伪逆

1. 用于非方阵求解线性方程问题
   Definition Moore-Penrose pseudoinverse，矩阵 $\mathbf{A}$ 的伪逆定义如下：

$${\mathbf{A}}^{+}=\underset{\alpha \searrow 0}{\lim }({\mathbf{A}}^T\mathbf{A}+\alpha \mathbf{I}{)}^{-1}{\mathbf{A}}^T$$
计算时，使用 ${\mathbf{A}}^{+}=\mathbf{V}{\mathbf{D}}^{+}{\mathbf{U}}^T$ ，其中 $\mathbf{U}$ 、 $\mathbf{D}$ 和 $\mathbf{V}$ 是矩阵 $\mathbf{A}$ 奇异值分解后得到的矩阵。对角矩阵 $\mathbf{D}$ 的伪逆 ${\mathbf{D}}^{+}$ 是其非零元素取倒数之后再转置得到的。

2. 对与线性方程 $\mathbf{A}\mathbf{x}=\mathbf{y}⟹\mathbf{x}=\mathbf{B}\mathbf{y}$
   • 当矩阵 $\mathbf{A}$ 的列数多于行数时，使用伪逆求解线性方程时众多可能解法中的一种。特别地 $\mathbf{x}={\mathbf{A}}^{+}\mathbf{y}$ 是方程所有可行解中Euclidean norm $||\mathbf{x}|{|}_2$ 最小的一个
   • 当矩阵 $\mathbf{A}$ 的列数少于行数时，可能没有解，通过伪逆得到的 $\mathbf{x}$ 使得 $\mathbf{A}\mathbf{x}$ 和 $\mathbf{y}$ 的Euclidean距离 $||\mathbf{A}\mathbf{x}-\mathbf{y}|{|}_2$ 最小

---

四、迹运算

1. 迹运算返回的是矩阵对角元素的和：

$$Tr(\mathbf{A})=\sum _i{\mathbf{A}}_{i,j}$$
2. 迹运算描述矩阵 $Frobenius$ 范数：

$$||\mathbf{A}|{|}_F=\sqrt{Tr(\mathbf{A}{\mathbf{A}}^T)}$$
3.

$$Tr(\mathbf{A}\mathbf{B}\mathbf{C})=Tr(\mathbf{C}\mathbf{A}\mathbf{B})=Tr(\mathbf{B}\mathbf{C}\mathbf{A})$$
更一般地：

$$Tr(\prod _{i=1}^n{\mathbf{F}}^{(i)})=Tr({\mathbf{F}}^{(n)}\prod _{i=1}^{n-1}{\mathbf{F}}^{(i)})$$
4. 即使循环转置后矩阵乘积得到的矩阵形状变了，迹运算地结果不变，假设矩阵 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ ，矩阵 $\mathbf{B}\in {\mathbb{R}}^{n\times m}$

$$Tr(\mathbf{A}\mathbf{B})=Tr(\mathbf{B}\mathbf{A})$$
尽管 $\mathbf{A}\mathbf{B}\in {\mathbb{R}}^{m\times m}$ 和 $\mathbf{B}\mathbf{A}\in {\mathbb{R}}^{n\times n}$

---

五、矩阵求导

1.行向量对元素求导

设$y^T=[y_1,...,y_n]$是$n$维行向量，$x$是元素，则$\frac{\partial y^T}{\partial x}=[\frac{\partial y_1}{\partial x},...,\frac{\partial y_n}{\partial x}]$

---

2.列向量对元素求导

设$y=\left[\begin{array}{c}{y}_1\\ ⋮\\ y_m\end{array}\right]$是$m$维列向量，$x$是元素，则$\frac{\partial y}{\partial x}=\left[\begin{array}{c}\frac{\partial y_1}{\partial x}\\ ⋮\\ \frac{\partial y_m}{\partial x}\end{array}\right]$

---

3.矩阵对元素求导

设$Y=\left[\begin{array}{ccc}{y}_{11}& \cdots & y_{1n}\\ ⋮& \ddots & ⋮\\ y_{m1}& \cdots & y_{mn}\end{array}\right]$是$m\times n$矩阵，$x$是元素，则

$$\frac{\partial Y}{\partial x}=\left[\begin{array}{ccc}\frac{\partial y_{11}}{\partial x}& \cdots & \frac{\partial y_{1n}}{\partial x}\\ ⋮& \ddots & ⋮\\ \frac{\partial y_{m1}}{\partial x}& \cdots & \frac{\partial y_{mn}}{\partial x}\end{array}\right]$$

---

4.元素对行向量求导

设$y$是元素，$X^T=[x_1,...,x_q]$是$q$维行向量，则$\frac{\partial y}{\partial X^T}=[\frac{\partial y}{\partial x_1},...,\frac{\partial y}{\partial x_q}]$

---

5.元素对列向量求导

设$y$是元素，$X=\left[\begin{array}{c}{x}_1\\ ⋮\\ x_p\end{array}\right]$是$p$维列向量，则$\frac{\partial y}{\partial X}=\left[\begin{array}{c}\frac{\partial y}{\partial x_1}\\ ⋮\\ \frac{\partial y}{\partial x_p}\end{array}\right]$

---

6.元素对矩阵求导

设$y$是元素，$X=\left[\begin{array}{ccc}{x}_{11}& \cdots & x_{1q}\\ ⋮& \ddots & ⋮\\ x_{p1}& \cdots & x_{pq}\end{array}\right]$是$p\times q$矩阵，则

$$\frac{\partial y}{\partial X}=\left[\begin{array}{ccc}\frac{\partial y}{\partial x_{11}}& \cdots & \frac{\partial y}{\partial x_{1q}}\\ ⋮& \ddots & ⋮\\ \frac{\partial y}{\partial x_{p1}}& \cdots & \frac{\partial y}{\partial x_{pq}}\end{array}\right]$$

---

7.行向量对列向量求导

设$y^T=[y_1,...,y_n]$是n维行向量，$X=\left[\begin{array}{c}{x}_1\\ ⋮\\ x_p\end{array}\right]$ 是$p$维列向量，则

$$\frac{\partial y^T}{\partial X}=\left[\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \cdots & \frac{\partial y_n}{\partial x_1}\\ ⋮& \ddots & ⋮\\ \frac{\partial y_1}{\partial x_p}& \cdots & \frac{\partial y_n}{\partial x_p}\end{array}\right]$$

---

8.列向量对行向量求导

设$y=\left[\begin{array}{c}{y}_1\\ ⋮\\ y_m\end{array}\right]$是$m$维列向量，$X^T=[x_1,...,x_q]$是$q$维行向量，则

$$\frac{\partial y}{\partial X^T}=\left[\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \cdots & \frac{\partial y_1}{\partial x_q}\\ ⋮& \ddots & ⋮\\ \frac{\partial y_m}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_q}\end{array}\right]$$

注：参考《Deep Learning》,lan Goodfellow, Yoshua Bengio, Aaron Courville