数学期望
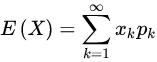
- 泊松分布的期望为λ
- 指数分布的期望为1/λ
随机变量函数的数学期望
E ( Y ) = E ( g ( X ) ) = ∫ − ∞ + ∞ g ( x ) f ( x ) d x E(Y)=E(g(X))=\int_{-\infty}^{+\infty}g(x)f(x)dx E(Y)=E(g(X))=∫−∞+∞g(x)f(x)dx
重要意义在于，求Y的期望时只需要利用X的分布律和概率密度函数即可
数学期望的特性
- E ( a X + b Y + c ) = a E ( X ) + b E ( Y ) + c E(aX+bY+c) = aE(X)+bE(Y)+c E(aX+bY+c)=aE(X)+bE(Y)+c
- 若X,Y相互独立，则有 E ( X Y ) = E ( X ) E ( Y ) E(XY)=E(X)E(Y) E(XY)=E(X)E(Y)
方差
定义：
V a r ( X ) = E ( [ X − E ( X ) ] 2 ) Var(X)=E([X-E(X)]^2) Var(
最低0.47元/天 解锁文章
扫一扫
1112
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
