参考线平滑算法解析及实现--U型弯道场景仿真调试

算法解析

场景：

 参考线平滑算法：：

（1）作用：

 routing结果：

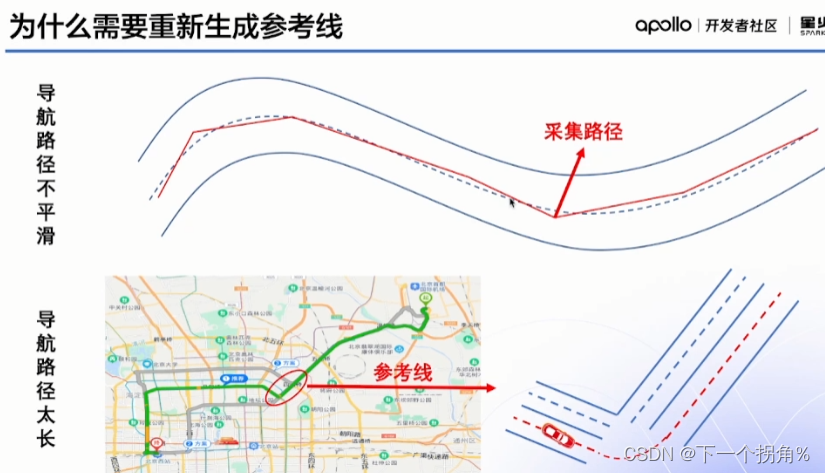
在没有道路不通行的情况下，routing的道路是不变的，；只有道路不通行的时候，planning会重新发送道路规划模块给routing，routing是一个全局的结果。

参考线在routing的基础上根据车辆周围障碍物和交规，取出其中一段作为参考线。

轨迹是在参考线中更为具体的一条，并且包含车辆的动态信息

Apollo的参考线referenceline数据结构：：

参考线的优先级：：再有多条参考线时，根据优先级挑选

 分段限速、参考点是“数组”

（vector：：容器，）

map_path_:地图中的参考线要做映射到planning中的参考线中，一一对应

1.

曲率影响车辆方向

2.

参考线提供者根据地图信息和pnc中车辆位置来生成

参考线生成：：

参考线平滑：：采用离散点的平滑

 可通过配置参数来选择平滑方法

参考线的平滑函数是在 ReferenceLine类的SmoothReferenceLine的函数中实现的：：
输入是raw_reference_line，输出是平滑后的reference_line，

中间经过产生中间点、平滑两个阶段实现，平滑算法在smoother的Smooth函数中实现

1. 设置中间点

 根据参考线x值进行均匀的采样，每一个中间点都会有path_point 和 横纵向裕度（裕度指：采样时点周围可以平移的空间），变量enforced是判断裕度是不是强约束，如是，则必须遵守裕度，在平滑过程中只有首尾两个点是强约束，别的点都不是强约束。

默认配置：纵向边界、横向边界（重要的）

2.平滑函数：：

参考线上的离散点有限的平移，对原始的参考线进行平滑。类DiscretePointsSmoothCofig中有两种不同的平滑算法，通过配置文件中的配置参数进行选择。

 （1）FemPosSmooth算法

输入：anchor point 中间点里面的x,y和横纵向裕度(raw_point2d ,bounds)

输出：平滑后的点（ptr_smoothed_point2d）

Solve函数进行求解：：

 三种求解方式，Apollo默认不考虑曲率约束，求解会快一些

平滑求解过程：：（二次优化问题）

 

红线越短约好，越平滑 

二次优化的约束条件：：： 

横纵向约束在bound_boxd的约束范围内

2.U型路口仿真测试

绘制对比路径：：

（1）记录行驶数据：

打开jupyter notebook，脚本在modules 的tools文件夹下

cyber_record记录：：cyber_recorder record -a 

车辆行驶完ctrl+c停止

ls 查看刚才录制的文件，将文件移动到tools所在的目录下：：

mv 20230108131647.record.0000 modules/tools/

20230108131647.record.0000就是本次录制的文件，所对应的参考线平滑的参数在 ：：

vim modules/planning/conf/discre**.pb.txt  

可以查看配置文件，调配置参数：：

 为了绘制对比，所以重启一下dream view，避免上次数据的混入。

【在这里面修改，按键“insert”，Esc退出,shift+进入命令格式。 ：q退出上面格式不保存，：wo保存退出,

linux界面显示insert怎么返回？ - 琴策网   】

bash 编译：：bash /apollo_workspace/scripts/bootstrap_neo.sh  restart

然后绘制路径，开启录制。

然后在

 工具中将这两个文件名修改成生成的两个，运行