数学知识（一）——数论(质数、约数)

前言

算法基础课-4.1

第四章 数学知识（一）
数论(质数、约数)
共7题，知识点如下：

质数：
试除法判定质数、
试除法分解质因数、
筛质数—埃氏筛法，线性筛法。

约数：
试除法求约数、
约数个数、
约数之和、
最大公约数—欧几里得算法。

质数和约数都属于数论

数论这章一定要把原理理解了，否则很难把题做出来

质数

试除法判定质数

时间复杂度一定是根号n

模板

bool is_prime(int x)
{
    if (x < 2) return false;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
            return false;
    return true;
}

模板题 AcWing 866. 试除法判定质数

#include <iostream>

using namespace  std;

bool is_prime(int n) {
    if (n < 2) return false;
    // 推荐使用i <= n / i
    // 原因：使用i <= sqrt(n) 每次会调用函数，速度很慢
    //       使用i * i <= n，当n接近int最大值时，i*i会爆int
    for (int i = 2; i <= n / i; i++) {
        if (n % i == 0) return false;
    }
    return true;
}

int main() {
    int n;
    cin >> n;
    while (n --) {
        int x;
        cin >> x;
        if (is_prime(x)) puts("Yes");
        else puts("No");
    }
    return 0;
}

试除法分解质因数

质因数: 在数论里是指能整除给定正整数的质数。

每个合数都可以写成几个质数相乘的形式,如 6=2*3, 8=2³ ,

这几个质数就叫做这个合数的质因数

时间复杂度可以比根号n小

比如 n 为 2^k ，进循环就除干净了 n=1，结束了，此时时间复杂度为 logn

如果有两个，乘一块就比n大了

模板

void divide(int x)
{
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
        {
            int s = 0;
            while (x % i == 0) x /= i, s ++ ;
            cout << i << ' ' << s << endl;
        }
    if (x > 1) cout << x << ' ' << 1 << endl;
    cout << endl;
}

模板题 AcWing 867. 分解质因数

#include <iostream>

using namespace  std;

// 输出每个质因数的底数和指数。
void divide(int n) {
    // 枚举所有于根号n的质因子
    for (int i = 2; i <= n / i; i++) {
        if (n % i == 0) { // i一定是质数
            // 统计次数(指数)
            int s = 0;
            while(n % i == 0) {
                n /= i;
                s ++;
            }
            printf("%d %d\n", i, s);
        }
    }
    // 处理剩下的，大于根号n的质因子
    if (n > 1) printf("%d %d\n", n, 1);
    puts("");
}

int main() {
    int n;
    cin >> n;
    while (n --) {
        int x;
        cin >> x;
        divide(x);
    }
    return 0;
}

筛质数

从前往后，将每个数后面所有是他倍数的数删去

如果p最后留下来了，说明1-p-1不存在任何p的约数

模板—朴素筛法求素数

int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i]) continue;
        primes[cnt ++ ] = i;
        for (int j = i + i; j <= n; j += i)
            st[j] = true;
    }
}

模板—线性筛法求素数

int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

模板题 AcWing 868. 筛质数

埃氏筛法

埃氏筛法
其实并不需要将2-p枚举一遍，只判断一下当中的质数即可

2-p-1中的质数只要不是p的约数，p就是一个质因数

不是质数的时候就不需要筛他的所有数的倍数

当n为2³²时，loglogn 才约等于5，所以是接近 O(n) 的

#include <iostream>

using namespace  std;

const int N = 1e6 + 10;

int primes[N], cnt;
bool st[N];

// 求出 1∼n 中质数的个数。
void get_primes(int n) {
    for (int i= 2; i <= n; i++) {
        if (!st[i]) { // 没被筛过，说明是质数
            primes[cnt ++] = n;
            // 删掉每个数的倍数
            for (int j = i + i; j <= n; j += i) st[j] = true;
        }
    }
}

int main() {
    int n;
    cin >> n;

    get_primes(n);
    
    cout << cnt << endl;
    return 0;
}

线性筛法

核心原理：保证每个数一定是被它的最小质因子筛掉

数据范围10⁷ 时候，速度比埃氏筛法快一倍左右

10⁶ 的时候，速度差不多

任何一个合数（非质数）都会被筛掉，而且只会用最小质因子来筛

而每个数都只有一个最小质因子

所以每个数只会被筛一次，所以是线性的

如果i是合数，碰到 primes[j]（最小质因子） ，就一定会停下来

i是质数时，碰到 primes[j] = i 的时候 ，也会停下来

#include <iostream>

using namespace  std;

const int N = 1e6 + 10;

int primes[N], cnt;
bool st[N];

// 求出 1∼n 中质数的个数。

void get_primes(int n) {
    for (int i= 2; i <= n; i++) {
        if (!st[i]) primes[cnt ++] = i;
        // 从小到大枚举所有质数
        for (int j = 0; primes[j] <= n / i; j++) {
            // 把当前质数和i的乘积筛掉
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break; // primes[j]一定是i的最小质因子（从小到大枚举的）

        }
    }
}

int main() {
    int n;
    cin >> n;

    get_primes(n);
    
    cout << cnt << endl;
    return 0;
}

不用纠结为啥这么筛，只需要知道

目的是比传统枚举到根号n速度要快即可

质数倍数是非质数

埃氏筛法：用0-n-1间的质数来排除没用的数（非质数一定可以整除某个质数）

线性筛法：用最小质因数排除（2357等）

一般都用线性筛法，但埃氏筛法的思路比较重要，可以用来解决其他问题

约数

算术基本定理

百度

维基

约数

约数也一定是成对出现的，枚举较小的即可

只需要枚举到根号n即可

可以通过每个数有多少个倍数，来求有多少约数

int 范围内，约数最大的，大约是1500个

试除法求所有约数

时间复杂度根号n

模板

vector<int> get_divisors(int x)
{
    vector<int> res;
    for (int i = 1; i <= x / i; i ++ )
        if (x % i == 0)
        {
            res.push_back(i);
            if (i != x / i) res.push_back(x / i);
        }
    sort(res.begin(), res.end());
    return res;
}

模板题 AcWing 869. 试除法求约数

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// 从小到大的顺序输出它的所有约数
vector<int> get_divisors(int n) {
    vector<int> res;
    
    for (int i = 1; i <= n / i; i++) {
        if (n % i == 0) { // i是n的约数
            res.push_back(i);
            // 防止加入重复的(比如9,是3的平方)
            if (i != n / i) res.push_back(n / i);
        }
    }
    sort(res.begin(), res.end());
    return res;
}

int main() {
    int n;
    cin >> n;
    
    while (n --) {
        int x;
        cin >> x;
        auto res = get_divisors(x);
        for (auto t : res) cout << t << " ";
        cout << endl;
    }
    return 0;
}

约数个数和约数之和

模板

如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数： (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和： (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)

模板题 AcWing 870. 约数个数,

分解方法：分别分解每一个

比如分解a1，将a1所有质因子找出来，然后累加次数即可

#include <iostream>
#include <algorithm>
#include <unordered_map>

using namespace std;

typedef long long LL;
const int mod = 1e9 + 7;

int main() {
    int n;
    cin >> n;
    
    unordered_map<int, int> primes; // 存所有底数和指数
    while (n --) {
        int x;
        cin >> x; // 对每一个a[i]
        // 累加所有质因子的出现次数
        for (int i= 2; i <= x / i; i++) {
            while (x % i == 0) {
                x /= i;
                primes[i] ++; // 存了所有质因数的指数
            }
        }
        // 处理大于根号n的质因数
        if (x > 1) primes[x] ++;
        
    }
    // 把所有指数+1相乘即可
    LL  res = 1;
    for (auto prime : primes) res = res * (prime.second + 1) % mod;
    
    cout << res << endl;
    
    return 0;
}

模板题 AcWing 871. 约数之和

两个公式是独立的

用乘法分配律展开，就是所有约数加到一块

#include <iostream>
#include <algorithm>
#include <unordered_map>

using namespace std;

typedef long long LL;
const int mod = 1e9 + 7;

int main() {
    int n;
    cin >> n;
    // 也要分解质因数
    unordered_map<int, int> primes; // 存所有底数和指数
    while (n --) {
        int x;
        cin >> x; // 对每一个a[i]
        // 累加所有质因子的出现次数
        for (int i= 2; i <= x / i; i++) {
            while (x % i == 0) {
                x /= i;
                primes[i] ++; // 存了所有质因数的指数
            }
        }
        // 处理大于根号n的质因数
        if (x > 1) primes[x] ++;
        
    }
    // 直接带入求和的公式即可
    LL  res = 1; // 每一个质因数相乘即可
    for (auto prime : primes)  {
        // p：质数的底数，a：质数的指数
        int p = prime.first, a = prime.second;
        LL t = 1; 
        // 第一次：【p+1】-->第二次：【p^2+p+1】--->第a次 【p^a +p^(a-1)+···+p+1】
        while (a --) t = (t * p + 1) % mod;
        res = res * t % mod;
    }
    
    cout << res << endl;
    
    return 0;
}

欧几里得算法

也叫辗转相除法

整除

a整除b写作a|b ,其实是 b ÷ a 余数为0

其中a是除数,b是a的倍数(被除数)

a与b 的公约数,就等于 b 和 a模b 的公约数

将a//b看成c
即可以将a mod b 转成 a - c*b

而d能整除b,所有可以把右边的约掉,只需要求d能整除a即可

所有左右两边的公约数是相等的

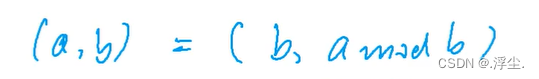
很常见，一定要记住该模板

欧几里得算法时间复杂度是 logn

模板

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

模板题 AcWing 872. 最大公约数

#include <iostream>

using namespace std;

int gcb(int a, int b) {
    // b如果不是0，返回b和a模b，是0就返回a，因为可以整除任何数
    return b ? gcb(b, a % b) : a;
}

int main() {
    int n;
    scanf("%d", &n);
    while (n --) {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", gcb(a, b));
    }
    return 0;
}

整除和除的区别