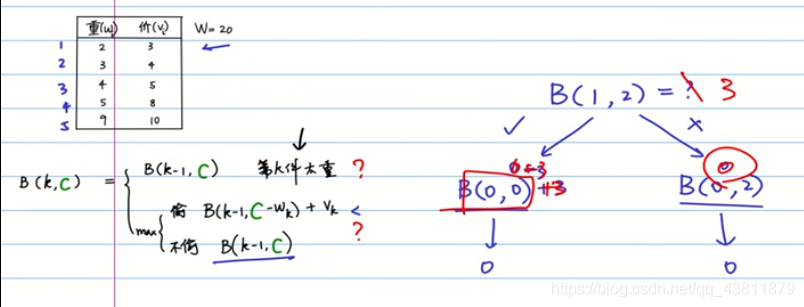
背包问题
该背包最大可以装20kg的物品,现在由5件商品重量和价格如上表所示,求出背包可以装下物品最大的价值
#include<bits/stdc++.h>
using namespace std;
#define W 21
#define N 6
int b[N][W];
int w[6]={0,2,3,4,5,9};//定义一个数组存每件物品的重量
int v[6]={0,3,4,5,8,10};//定义一个数组存每件物品的价值
void knapsack(){
for(int k=1;k<N;k++)
{
for(int c=1;c<W;c++)
{
if(w[k]>c)
{
b[k][c]=b[k-1][c];
}//第k件太重,背包无法装下
else{
int value1=b[k-1][c-w[k]]+v[k];//value1是指拿第k件物品后的价值
int value2=b[k-1][c];//value2是指不拿第k个物品后的价值
if(value1>value2)
{
b[k][c]=value1;
}
else{
b[k][c]=value2;
}
}
}
}
}
int main()
{
knapsack();
cout<<b[5][20];
return 0;
}
二维数组里面存放的数如下图所示:
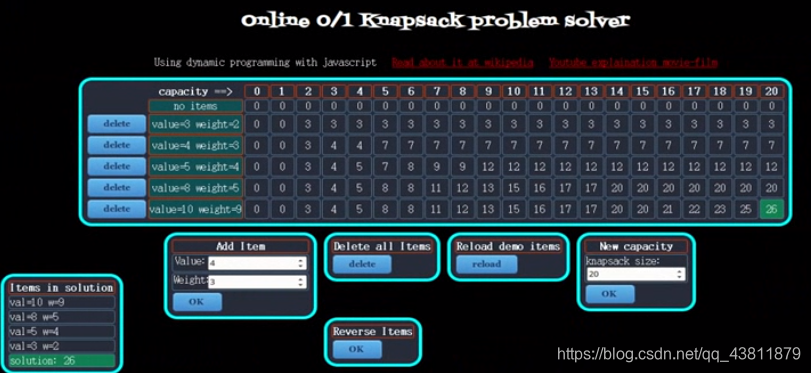










 本文介绍了一种使用动态规划解决背包问题的方法,通过给定的物品重量和价值,求解在背包容量限制下能获得的最大价值。示例中,背包容量为20kg,包含5件商品,通过二维数组记录不同容量下背包能容纳的最大价值。
本文介绍了一种使用动态规划解决背包问题的方法,通过给定的物品重量和价值,求解在背包容量限制下能获得的最大价值。示例中,背包容量为20kg,包含5件商品,通过二维数组记录不同容量下背包能容纳的最大价值。
















 2775
2775

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








