实数序列频谱的共轭对称性(DFT与IDFT仿真实现)

一、基础知识

1、傅里叶变换：通俗来讲，是以时间为自变量的信号与以频率为自变量的“频谱函数”之间的某种转换关系。

DFT：即离散傅里叶变换，对离散序列进行傅里叶变换。设x(n)为长度为M的有限长序列，其N点DFT定义(公式)：

 

 其中         N 是DFT变换区间长度，其中X(0)和X(N/2)应为实数。

 说明：

1.两个定义式均出现两个变量k,n。

n为变量时，对所有的n加权求和得到一个X(k),共N个；

k为变量时，对所有的k加权求和得到一个x(n),共N个；

2.DFT的变换结果与变换长度N有关。

 2、实数序列的频谱应当是共轭对称的

设X(K)为序列频谱，N为总点数，则应满足X(K) = X(N - K) 或者  X*(jw) = X(-jw)

证明：

实信号x(t) 等于它的共轭x*(t)

所以x(t) 的傅氏变换X(f)等于

x*(t)的傅氏变换X*(-f)

所以X*(-f)等于X(f)

---

二、问题描述

描述问题：

刚开始构造实数序列频谱时，频谱序列共计N个点，举例：N=8；

设a为实数序列频谱，b为实数序列，利用构造好的频谱序列a通过IDFT(逆离散傅里叶变换)得到实数序列。

这里需要注意：频谱序列特点：

1.必须是共轭对称性，X(k) = X*(N-k)

2.当k=0或N/2时，必须为实数，物理意义代表实数序列的求和。

注：刚开始时我以为只要符合共轭对称就行，所以构造的a频谱序列是对称且共轭，没有考虑到k=0和k=N/2的情况！因此，导致IDFT后得到的序列并不是实数序列。

a = [1+5j 2+4j 3-5j  3-5j 3+5j 3+5j 2-4j 1-5j]
b = ifft(fftshift(a))

---

 

三、原因分析：

实数序列的频谱满足的条件：

1.共轭对称性。

2.k=0和k=N/2时频谱值为实数，物理意义为序列的和。

---

四、解决方案：

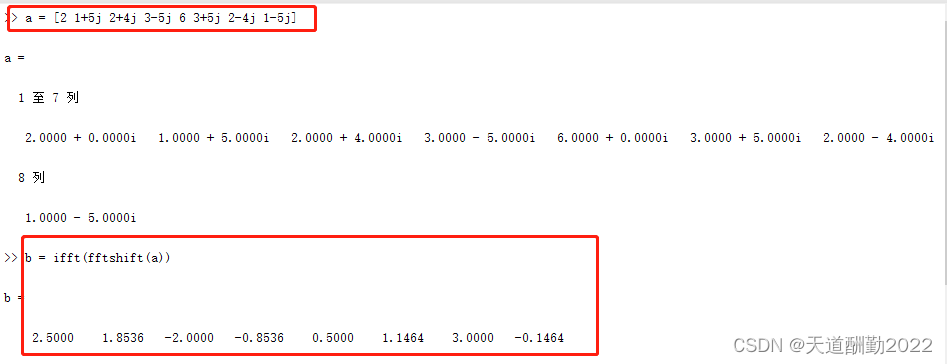
 a = [2 1+5j 2+4j 3-5j 6 3+5j 2-4j 1-5j]

 b = ifft(fftshift(a))

 b =

    2.5000    1.8536   -2.0000   -0.8536    0.5000    1.1464    3.0000   -0.1464