最长回文问题

一、最长回文子串

  最长回文子串的问题描述：
  给出一个字符串 S ，求 S 的最长回文子串的长度。
  样例：
  字符串"PATZJUJZTACCBCC"的最长回文子串为"ATZJUJZTA"，长度是9
方法一：
  暴力出奇迹，O(n³)，枚举子串的两个端点 i 和 j，判断在[i,j]区间内的子串是否为回文。
方法二：
  转化为LCS问题：把字符串 S 倒过来变成字符串 T ，然后对 S 和 T 进行LCS模型求解，得到的结果就是需要的答案。而事实上这种做法是错误的，因为一旦 S 中同时存在一个子串是它的倒序，那么答案就会出错。
  例如字符串 S = “ABCDZJUDCBA”，将他倒置就是 T = “ABCDUJZDCBA”，这样得到最长公共子串就是 “ABCD”，长度为 4 ，而事实上 S 的最长回文子串长度为 1。
方案三：
  动态规划，O(n²)，令dp[i][j]表示 S[i] 至 S[j] 所表示的子串是否是回文子串，是则为 1，不是则为 0.
状态转移方程：
$$dp[i][j]=\{\begin{array}{ll}dp[i+1][j-1]& \text{s[i]==s[j]}\\ 0& \text{s[i]!=s[j]}\end{array}$$
具体代码：

#include<cstdio>
#include<cstring>
const int maxn = 1010;
char s[maxn];
int dp[maxn][maxn];
int main(void)
{
    gets(s);
    int len = strlen(s),ans = 1;
    memset(dp,0,sizeof(dp));    //dp数组初始化为0
    //边界
    for(int i=0;i<len;i++){
        dp[i][i] = 1;
        if(i<len-1){
            if(s[i]==s[i+1]){
                dp[i][i+1] = 1;
                ans = 2;    //初始化时应注意当前最长回文子串长度
            }
        }
    }
    //状态转移方程
    for(int l=3;l<=len;l++){
        for(int i=0;i+l-1<len;i++){
            int j = i+l-1;
            if(s[i]==s[j]&&dp[i+1][j-1]){
                dp[i][j] = 1;
                ans = l;    //更新最长回文子串长度
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}

方法三：
  二分+字符串hash，O(nlogn)，(⊙o⊙)…代码量有点长，可以自行了解
方法四：
  Manacher算法，O(n)
本文参考于 https://www.cnblogs.com/lykkk/p/10460087.html
先分析优化后的暴力不足：
  1、对于长度为奇数的回文和长度为偶数的回文，他们的对称轴是不一样的，要分类讨论。
  2、有些子串会被访问多次。
  比如：

char	a b a b a b a ……
i	0 1 2 3 4 5 6 ……

  我们枚举到第 i 位：
  i = = 3时第一个"aba"被遍历一次
  i = = 4时第一个"aba"又被遍历一次
  i = = 5时第一个"aba"双被遍历一遍
  …… ……
  i = = len/2时第一个"aba"又双叒叕被遍历一遍
一、处理字符串长度的奇偶性带来的对称轴不确定问题
  如果字符串的长度都是奇数就好办了
  处理原来的字符串，在收尾的所有空隙插入一个相同的无关的字符，插入后原字符串中是回文的子串还是回文串，不是回文的子串依旧不是。
  但是字符串的长度都变成了 2 * len+1，都成了奇数
  为什么是 2 * len+1，因为有 len-1 个空，开头和结尾又分别插入了2个，加起来等于 len + (len-1) + 2 = 2*len+1.
如：

长度为奇数的字符串
ababa —> @a#b#a#b#a#
长度为偶数的字符串
1221 —> @1#2#1#2#

’@'用来防止越界
二、找最长回文串
  回文半径：把一个回文串中最左或者最右位置的字符到其对称轴的距离称为回文半径
  在Manacher算法中，我们用 p[i] 表示第 i 个字符的回文半径

char	# a # b # c # b # a #
p[i]	1 2 1 2 1 6 1 2 1 2 1
p[i] - 1	0 1 0 1 0 5 0 1 0 1 0
i	1 2 3 4 5 6 7 8 9 10 11

  显然，最大值得p[i]-1就是答案

显然这个结论非常不显然，单从数值上来看的话，插入完字符之后对于一个回文串的长度为原串长度2 + 1,等于这个回文串半径2+1，显然相等

这样我们的问题就转化成了怎样快速的求出p数组
在这里我们利用回文串的对称性扩展回文串，p[i]不再直接赋值为1，而是根据之前求出的p[j]，0<j<i。
我们这里用mx表示所有字符产生的最大回文子串的最大右边界，id表示产生这个最大右边界的对称轴的位置。

为什么要维护这些东西，因为我们要利用回文串的对称性来更新当前位置的值，维护右边界（mx）后就可以直接判断当前位置是否可以直接利用对称性来更新（因为之前找到的回文串最右端就是到mx，超出mx的话就不能利用对称性来更新了）；id是对称轴，用来求关于i对称的位置j。

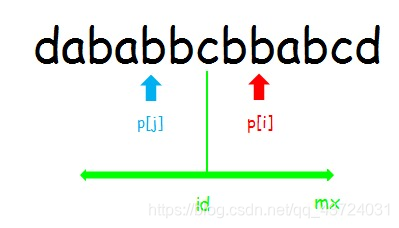
中间的#懒得画了就
如图，假设我们已经求出了p[1…7]，当i<mx时，因为id被更新过了，而i是id之后的位置，第i个字符一定落在id的右边，毋庸置疑。但这是我们关心的还是i是在mx的左边还是右边。

以下内容为了方便我们定义：
串 i 表示以 i 为对称轴的回文串(用红色的箭头表示)；
串 j 表示以 j 为对称轴的回文串(用蓝色的箭头表示)；
串 id 表示以 id 为对称轴的回文串(用绿色的箭头表示)；
情况1：i < mx
如上图，利用回文串的性质，对于 i，我们可以找到一个关于id对称的位置j=id∗2−i，进行加速查找但在这里又细分为了三种情况
(1)

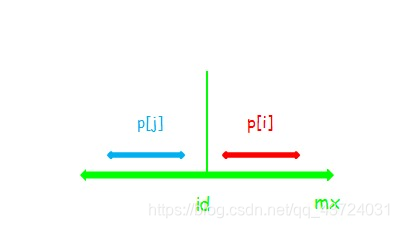
显然此时p[i]=p[j]。
对于这种情况，串i不可以再向两边扩张。
如果可以向两边扩张的话，p[j]也可以再向两边扩张，而p[j]已经确定了，所以串i不向两边扩张。
(2)

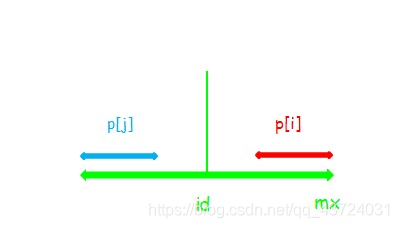
显然此时p[i]=p[j]
与(1)不同的是，串i是可以再向两边扩张的。
应该很显然，一比划就知道。
(3)

此时p[i]=mx−i
这时我们只能确定串i在mx以内的部分是回文的，并不能确定串i和串j相同。
同样，这时我们的串i是不可以再向两端扩张的。

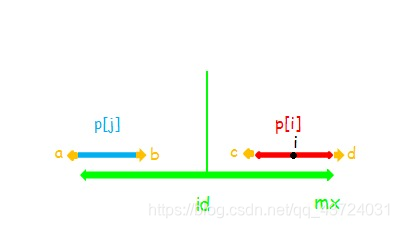
如果串i可以扩张，如图，则d=c，根据对称性c=b，又因为a=b，所以a=d，可以看到，串id可以继续扩张，因为p[id]已经固定了，所以串i不可以继续扩张
情况2：i >= mx

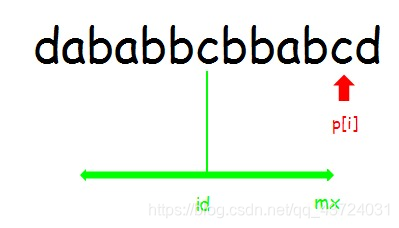
这时之前记录的信息都用不上了，于是p[i]=1。

if(i<mx)	p[i] = min(p[id*2-i],mx-i);	//情况1
else p[i] = 1;	//情况2
while(str[i+p[i]]==str[i-p[i]])	p[i]++;	//暴力拓展
if(p[i]+i>mx){	//更新id的位置
	 mx = p[i]+i;
	 id = i;
}

模板

P3805 【模板】manacher算法

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<map>
#include<queue>
#include<utility>
#include<set>
#include<stack>
#include<string>
#include<vector>
#define ll long long
#define llu unsigned long long
using namespace std;
const int maxn = 22000010;
char s[maxn],str[maxn];
int p[maxn];
int Init()
{
    int len = strlen(s);
    str[0] = '@',str[1] = '#';
    int j = 2;
    for(int i=0;i<len;++i){
        str[j++] = s[i];
        str[j++] = '#';
    }
    str[j] = 0;
    return j;
}
int manacher()
{
    int mx,id;
    mx = id = 0;
    int ans = -1;
    int len = Init();

    for(int i=1;i<len;i++){
        if(i<mx) p[i] = min(p[id*2-i],mx-i);
        else p[i] = 1;
        while(str[i+p[i]]==str[i-p[i]]) p[i]++;
        if(p[i]+i>mx){
            mx = p[i] + i;
            id = i;
        }
        ans = max(p[i]-1,ans);
    }
    return ans;
}
int main(void)
{
    cin>>s;
    cout<<manacher();
    return 0;
}